Учитель информатики
Информатика. 10 класса. Босова Л.Л. Оглавление
§13. Представление чисел в компьютере
Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).
Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.
2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
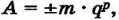
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 000 000 может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 10 9 .
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 10 1111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
Вот схема типичного транзистора:
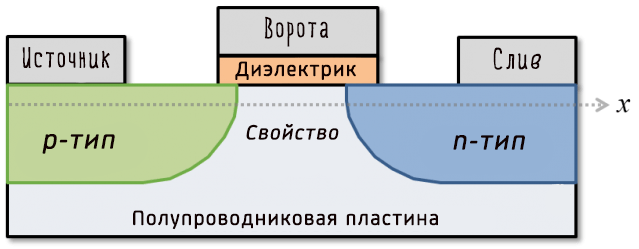
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).
Переведите данное число из десятичной системы счисления в двоичную, восьмиричную и шестнадцатиричную системы счисления 250(10)?
Переведите данное число из десятичной системы счисления в двоичную, восьмиричную и шестнадцатиричную системы счисления 250(10).

Преобразования чисел
Преобразования чисел В случае встроенных числовых типов (sbyte, int, float и т.д.) явное преобразование требуется тогда, когда вы пытаетесь сохранить большее значение в меньшем контейнере, поскольку при этом может происходить потеря данных. По сути, это способ сказать
СОРТИРОВКА ЧИСЕЛ Одним из наиболее распространенных тестов для машин является сортировка. Мы хотим разработать программу для сортировки целых чисел. Снова применим принцип черного ящика и подумаем в терминах ввода и вывода. Наш общий замысел, показанный на рис. 10.4,
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
В Древнем Египте использовались специальные символы (цифры) для обозначения чисел 1, 10, 10 2 , 10 3 , 10 4 , 10 5 , 10 6 , 10 7 . Вот некоторые из них:
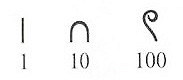
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:

Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:
Теперь число 3632 следует записывать, как:

Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
- Значение числа равно сумме значений его цифр. Например, число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2=32
- Если слева от большей цифры стоит меньшая, то значение равно разности между большей и меньшей цифрами. При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
- Значение равно сумме значений групп и цифр, не подходящих под 1 и 2 пункты.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.



Кодирование информации вокруг нас
Кодирование информации — это удел не только компьютерной техники. Мы очень часто сталкиваемся с этим явлением, и, порой, этого совсем не замечаем.
Не так уж давно мы пользовались телеграфом (эта услуга остается и по сей день). При этом отправляемый текст кодируется в виде последовательностей так называемых «точек» (коротких сигналов) и «тире» (длинных сигналов), отправляется по проводам. На выходе все это декодируется и печатается на ленте.
Многие люди в недавнем прошлом обязаны были знать эту кодировку, называемую иначе «Азбукой Морзе» по имени ее изобретателя.
В музыке информация много веков кодируется с помощью нотной записи (ноты). Математические формулы используются в математике. В химии применяются химические формулы. Таких примеров кодирования информации можно привести очень много.
По сравнению с приведенными примерами, кодировка, применяемая для компьютеров, выглядит намного проще, так как в ней используются только «нули» и «единицы».
Сравнительная простота кодирования обеспечивает все многообразие представляемой в компьютере информации (от простых текстов до сложнейших графических игр и видеофильмов). Это обусловлено высочайшим быстродействием компьютеров и их способностью к почти мгновенной обработке огромных массивов данных.












