Коэффициент детерминации рассчитывается для оценки качества подбора уравнения регрессии. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%. Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими. Значение коэффициента детерминации R 2 = 1 означает функциональную зависимость между переменными.
Для линейной зависимости коэффициент детерминации равен квадрату коэффициента корреляции rxy: R 2 = rxy 2 .
2 «>Рассчитать свое значение
Например, значение R 2 = 0.83, означает, что в 83% случаев изменения х приводят к изменению y . Другими словами, точность подбора уравнения регрессии — высокая.
В общем случае, коэффициент детерминации находится по формуле: или
В этой формуле указаны дисперсии:
,
где ∑(y- y ) — общая сумма квадратов отклонений;
— сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
— остаточная сумма квадратов отклонений.
В случае нелинейной регрессии коэффициент детерминации рассчитывается через этот калькулятор. При множественной регрессии, коэффициент детемрминации можно найти через сервис Множественная регрессия
Пример . Дано:
- доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и в покупку валюты, в общей сумме среднедушевого денежного дохода, % (Y)
- среднемесячная начисленная заработная плата, тыс. руб. (X)
Следует выполнить: 1. построить поле корреляции и сформировать гипотезу о возможной форме и направлении связи; 2. рассчитать параметры уравнений линейной и A1; 3. выполнить расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят B2 % от их среднего уровня; 4. оценить тесноту связи с помощью показателей корреляции и детерминации, проанализировать их значения; 5. Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом; 6. Оценить с помощью средней ошибки аппроксимации качество уравнений; 7. Оценить надежность уравнений в целом через F-критерий Фишера для уровня значимости а = 0,05. По значениям характеристик, рассчитанных в пп. 5,6 и данном пункте, выберете лучшее уравнение регрессии и дайте его обоснование.
- Решение онлайн
- Видео решение
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим
Анализ точности определения оценок коэффициентов регрессии
S a = 3.3432
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-557.64;913.38)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Статистическая значимость коэффициента регрессии b не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(a — t a S a; a + t aS a)
(17.1616;29.2772)
(b — t b S b; b + t bS b)
(-136.4585;445.7528)
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Коэффициент детерминации в Excel (Эксель)
Для статистических моделей во многих случаях необходимо определить точность прогноза. Это производится с помощью специальных расчётов в Microsoft Excel, а использоваться будет коэффициент детерминации. Он обозначается как R^2.
Статистические модели можно разделить на качественные уровни в зависимости от коэффициента. От 0.8 до 1 относятся модели хорошего качества, модели достаточного качества имеют уровень от 0.5 до 0.8, а плохое качество имеет диапазон от 0 до 0.5.
Способ определения точности с помощью функции КВПИРСОН
В линейной функции коэффициент детерминации будет равен квадрату корреляционного коэффициента. Рассчитать его можно с помощью специальной функции. Для начала создадим таблицу с данными.
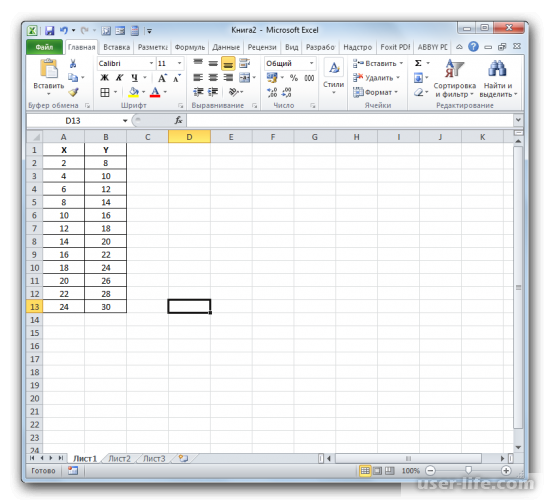
Потом нужно выбрать место, где будет показан результат расчёта и нажимаем на кнопку вставки функции.

После этого откроется специальное окно. Категорию нужно выбрать «Статистические» и выбираем КВПИРСОН. Эта функция позволяет определить коэффициент корреляции касательно функции Пирсона, соответственно квадратное значение коэффициента корреляции = коэффициенту детерминации.
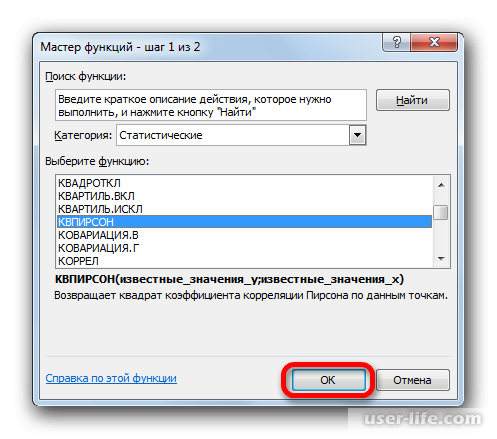
После подтверждения действия, появится окно в котором нужно в полях выставить «Известные значения Х» и «Известные значения Y». Нажимаем мышкой поле «Известные значения Y» и в рабочем окне выделяем данные столбца Y. Аналогичное действие делаем и с другим полем выбирая данные уже с таблицы Х.
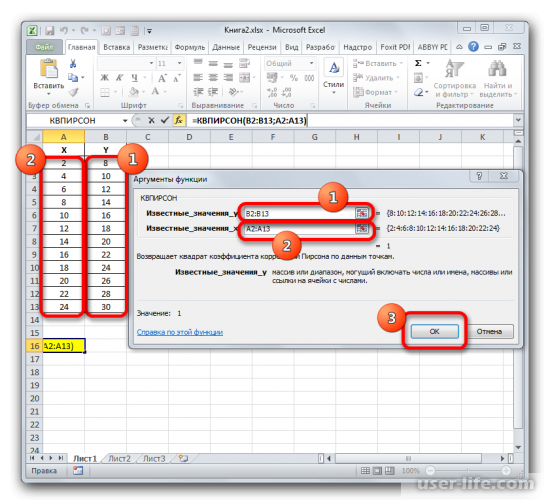
Как результат этих действий будет показано значение коэффициента детерминации в ячейке, которая ранее была выбрана для отображения результата.
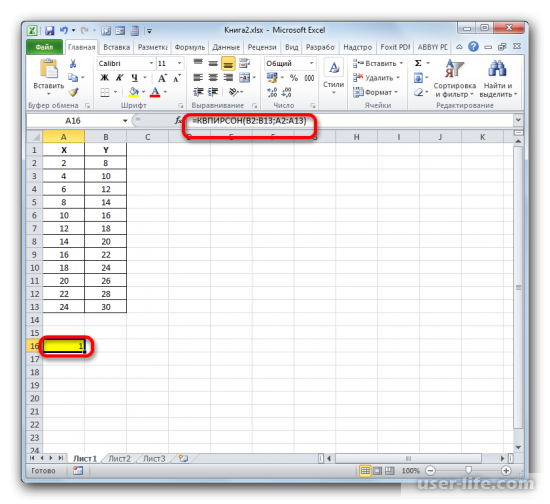
Определение коэффициента детерминации если функция не является линейной.
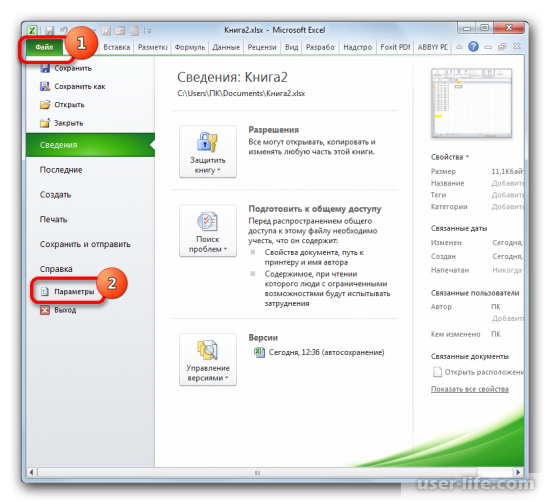
Если функция нелинейная, то инструментарий Excel также позволяет рассчитать коэффициент с помощью инструмента «Регрессия». Его можно найти в пакете анализа данных. Но для начала нужно активировать этот пакет, перейдя в раздел «Файл» и в списке открыть «Параметры».
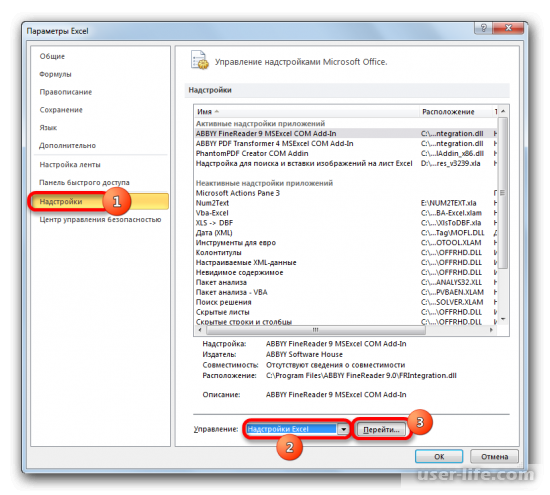
После этого можно увидеть новое окно, в котором нужно в меню выбрать «Надстройки», а в специальном поле по управлению надстройками выбираем «Надстройки Excel» и переходим к ним.
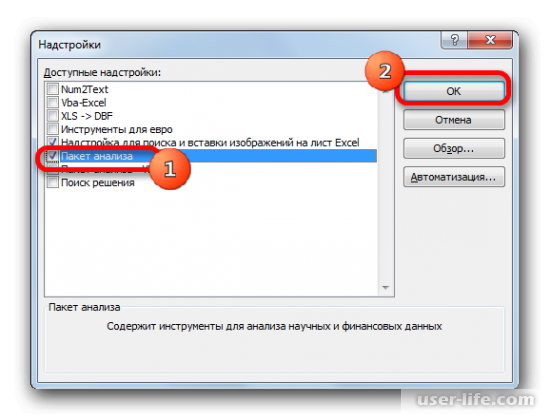
После перехода в надстройки Excel появится новое окно. В нём можно увидеть доступные для пользователя надстройки. Ставим галочку возле «Пакет анализа» и подтверждаем действие.
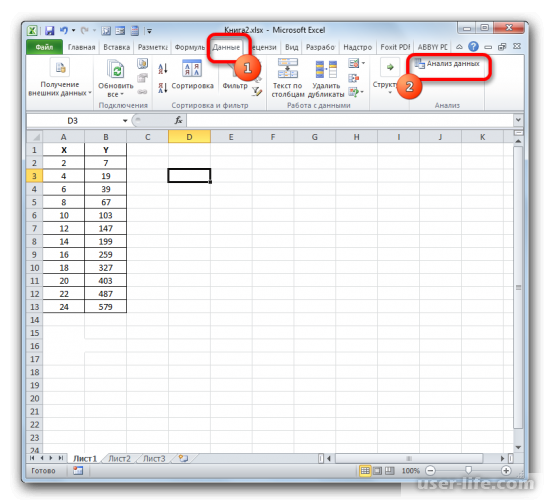
Найти его можно в разделе «Данные», после перехода в который нажимаем на «Анализ данных» в правой части экрана.
После его открытия, в списке выбираем «Регрессия»и подтверждаем действие.
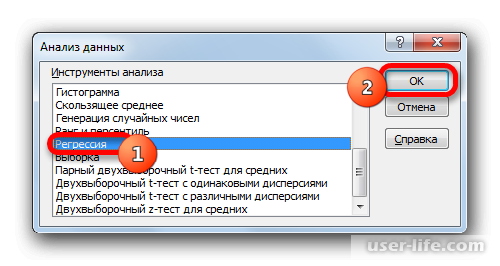
После этого появится новое окно в котором можно производить настройки. Входные данные позволяют настроить значение интервалов Х и Y, достаточно выделить соответствующие ячейки аргументов другого аргумента. В поле уровня надежности можно выставить нужный показатель. Параметры вывода позволяют задать где будет показан результат. Если к примеру выбрать показ на текущем листе, то для начала нужно выбрать пункт «Выходной интервал» — и нажать на области основного окна где будет в будущем отображаться результат и координаты ячейки будут показаны соответствующем поле. В конце подтверждаем действие.
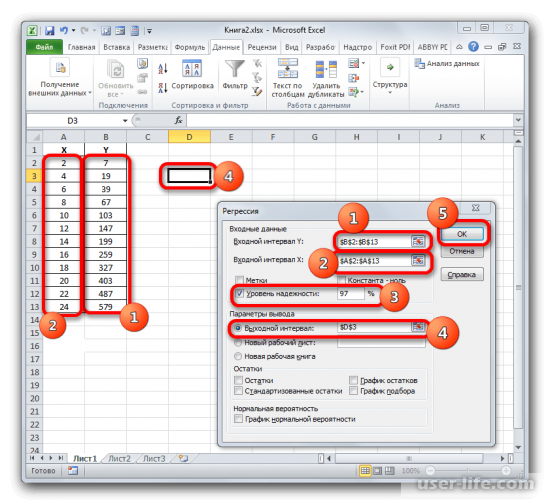
В рабочем окне появится результат. Так как мы вычисляем коэффициент детерминации, то в итогах нам нужен R-коэффициент. Если посмотреть на значение, то можно увидеть что оно относится к наилучшему качеству.
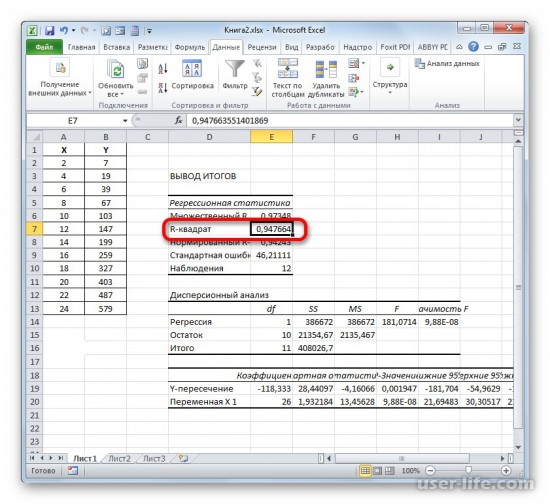
Способ определения коэффициента детерминации для линии тренда
Имея созданную таблицу с соответствующими значение, создаем график. Чтобы провести на нём линию тренда надо нажать на график, а именно на область где строится линия. Сверху в панели инструментов выбрать раздел «Макет», а в нём выбрать «Линия тренда». После этого в контексте данного примера в списке выбираем «Экспоненциальное приближение».
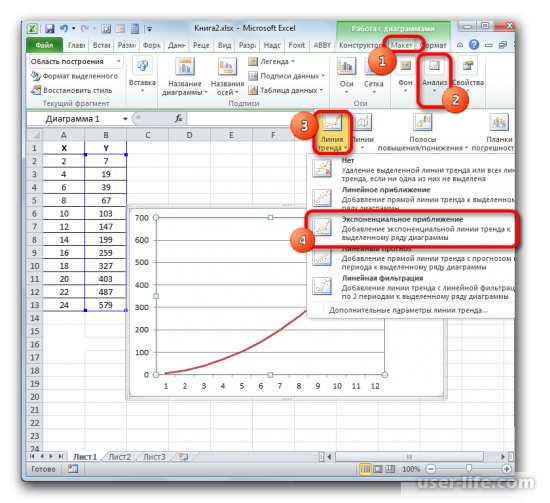
Линия тренда будет отображена на графике как кривая с черным цветом.
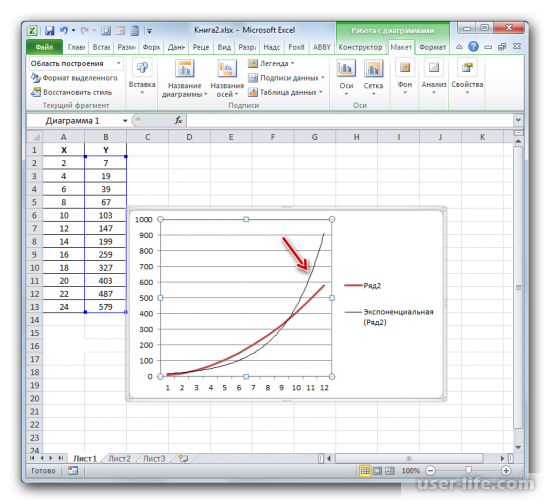
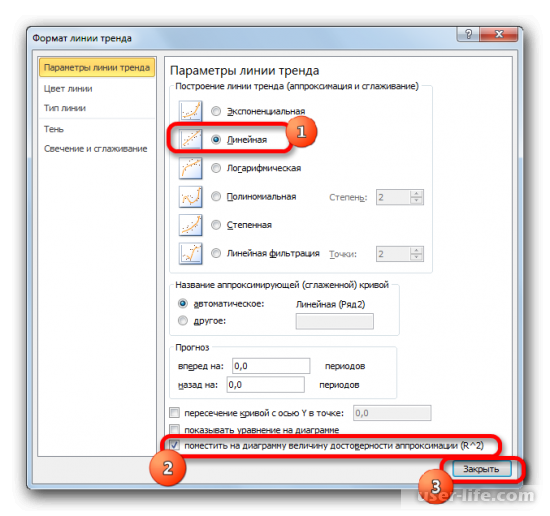
Для того чтобы показать коэффициент детерминации, нужно по черной кривой нажать правой кнопкой мыши и выбрать в списке «Формат линии тренда».
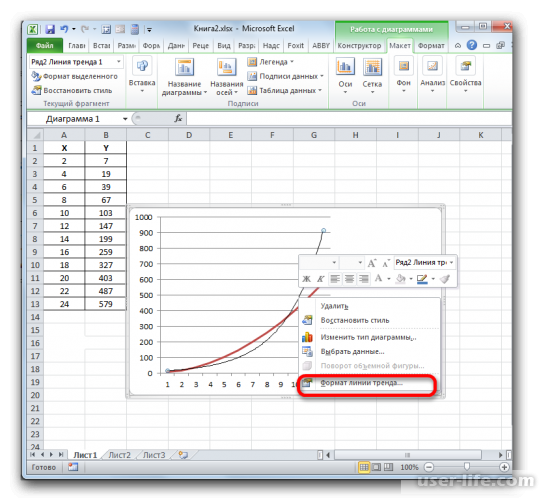
После этого появится новое окно. В нём нужно отметить флажком и выбрать нужное действие (показано на скриншоте). Благодаря этому коэффициент будет отображен на графике. После того как это было сделано, закрываем окно.
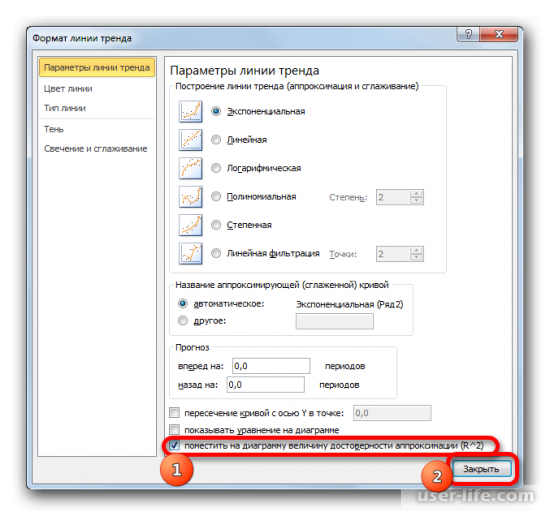
После закрытия окна формата линии тренда в рабочем окне можно увидеть значение коэффициента детерминации.
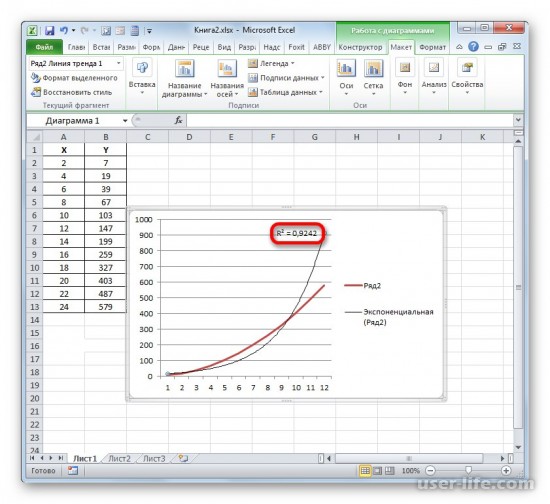
Если пользователю нужен другой типаж линии тренда, то в окне «Формат линии тренда» можно выбрать его. Не забыв задать его ранее при создании линии тренда в разделе «Макет» или в контекстном меню. Также не забываем ставить флажок для функции R^2.
Как результат можно увидеть изменение линии тренда и число достоверности.
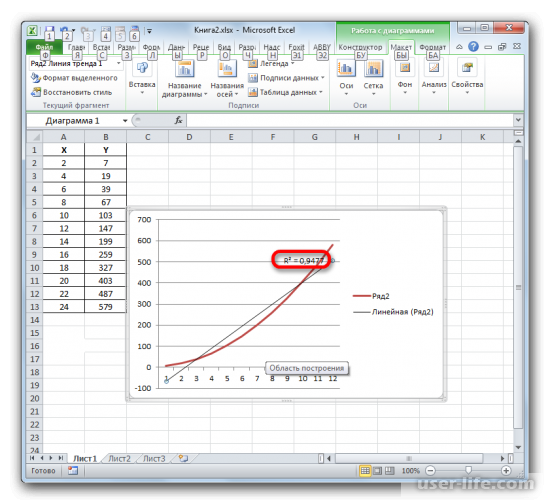
После просмотра разных вариаций линий тренда, пользователь может определить наиболее подходящую для себя так как показатель достоверности может меняться в зависимости от выбора линии. Максимальный коэффициент это единица, что означает максимальную достоверность, однако не всегда можно достигнуть этого значения.
Так было рассмотрено несколько способов по нахождению коэффициента детерминации. Пользователь может выбрать наиболее оптимальный для своих целей.
Алгоритм вычисления коэффициента выборочной детерминации в MS-Excel Текст научной статьи по специальности « Математика»

- Математика
Аннотация научной статьи по математике, автор научной работы — Красильников Дмитрий Евгеньевич
Рассматривается коэффициент выборочной детерминации как критерий однородности выборок в социально-экономических исследованиях. Приводится геометрическое доказательство закона разложения дисперсии , предлагается алгоритм вычисления коэффициента выборочной детерминации в MS-Excel, рассматривается случай, когда закон разложения дисперсии не выполняется, показана связь между коэффициентом выборочной детерминации и эмпирическим корреляционным отношением .
Похожие темы научных работ по математике , автор научной работы — Красильников Дмитрий Евгеньевич
Текст научной работы на тему «Алгоритм вычисления коэффициента выборочной детерминации в MS-Excel»
Д. Е. Красильников
АЛГОРИТМ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА ВЫБОРОЧНОЙ ДЕТЕРМИНАЦИИ
Нижегородский почтамт. Отделение почтовой связи №24
Рассматривается коэффициент выборочной детерминации как критерий однородности выборок в социально-экономических исследованиях. Приводится геометрическое доказательство закона разложения дисперсии, предлагается алгоритм вычисления коэффициента выборочной детерминации в MS-Excel, рассматривается случай, когда закон разложения дисперсии не выполняется, показана связь между коэффициентом выборочной детерминации и эмпирическим корреляционным отношением.
Ключевые слова: коэффициент выборочной детерминации, закон разложения дисперсии, MS-Excel, критерий однородности выборок, дисперсионный анализ, эмпирическое корреляционное отношение.
При проведении социологических, психологических, экономических и маркетинговых исследований почти всегда встает вопрос о репрезентативности исследуемой выборки. Под репрезентативностью выборки, чаще всего, понимается ее однородность. При этом в современной литературе по соответствующим дисциплинам не дается универсальный метод проверки гипотезы об однородности. Как правило, для такой проверки используют так называемый ¿-критерий, F-критерий или критерий «Хи-квадрат» (см., например, [1]), которые базируются на сравнении средних величин со значением функции Стьюдента, Фишера или Хи -квадрат. Однако эти критерии слабо чувствительны к социально-экономическим данным ввиду небольшого разброса значений таких данных, а применение указанных функций недостаточно обосновано, так как эти критерии были разработаны для биологических, а не социально-экономических исследований.
Другим распространенным подходом к оценке репрезентативности является обоснованность выборки с позиций той или иной задачи. Например, при изучении спроса на автомобили стоимостью от миллиона рублей выборка, сделанная из лиц с доходом 8-10 тыс. руб. , будет всегда нерепрезентативной.
Тем не менее, в Советском Союзе была разработана специальная статистика (функция от выборочной совокупности), позволяющая оценить однородность любой выборки при условии ее стратификации — коэффициент выборочной детерминации (^2выб). Его не следует путать с коэффициентом детерминации (R2 ), который характеризует качество аппроксимации с помощью линейной функции и не имеет отношения к выборочному методу.
Данная статистика основана на разложении дисперсии на межгрупповую и внутриг-рупповую. Это разложение также используется в дисперсионном анализе. «Первоначально (1918 г.) дисперсионный анализ был разработан английским математиком-статистиком Р.А. Фишером для обработки результатов агрономических опытов по выявлению условий получения максимального урожая различных сортов сельскохозяйственных культур. Сам термин «дисперсионный анализ» Фишер употребил позднее [2, с. 392].
Чтобы понять, на чем основано разложение дисперсии, рассмотрим так называемый «прямоугольный выборочный план», используемый в однофакторном дисперсионном анализе (табл. 1).
Этот план представляет собой таблицу, в которой каждый столбец является выборкой с n элементами. Всего делается m таких выборок. В литературе эти столбцы часто называют факторами, группами или стратами, а само расположение элементов выборок — стратификацией.
© Красильников Д. Е., 2016.
В этой статье при обозначении элемента таблицы символом у, первый индекс указывает номер строки, а второй — номер столбца, в соответствии с правилом обозначения элементов матриц, принятым в Советском Союзе. Замечу, что в английской традиции принята обратная запись, то есть сначала пишут столбец, а затем строку, а в современной российской литературе встречаются оба варианта.
Очевидно, что общее число элементов в таблице N есть
Прямоугольный выборочный план
1 у11 у12 уЦ у 1т
2 у21 у22 у 2 i у 2т
1 у,1 у 2 у, у гт
п уп1 уп 2 у п] у пт
Среднее у1 у 2 у, у т
По каждому столбцу вычисляется среднее арифметическое у. (внутригрупповая средняя), которое заносится в последнюю строку таблицы,
Матрица парных коэффициентов корреляции
Матрица парных коэффициентов корреляции представляет собой матрицу, элементами которой являются парные коэффициенты корреляции. Например, для трех переменных эта матрица имеет вид:
| — | y | x1 | x2 | x3 |
| y | 1 | ryx1 | ryx2 | ryx3 |
| x1 | rx1y | 1 | rx1x2 | rx1x3 |
| x2 | rx2y | rx2x1 | 1 | rx2x3 |
| x3 | rx3y | rx3x1 | rx3x2 | 1 |
Вставьте в поле матрицу парных коэффициентов.
Пример . По данным 154 сельскохозяйственных предприятий Кемеровской области 2003 г. изучить эффективность производства зерновых (табл. 13).
Задание
- Определите факторы, формирующие рентабельность зерновых в сельскохозяйственных предприятий в 2003 г.
- Постройте матрицу парных коэффициентов корреляции. Установите, какие факторы мультиколлинеарны.
- Постройте уравнение регрессии, характеризующее зависимость рентабельности зерновых от всех факторов.
- Оцените значимость полученного уравнения регрессии. Какие факторы значимо воздействуют на формирование рентабельности зерновых в этой модели?
- Оцените значение рентабельности производства зерновых в сельскохозяйственном предприятии № 3.
Решение получаем с помощью калькулятора Уравнение множественной регрессии :
Матрица X T
Умножаем матрицы, (X T X)
| 22 | 19.76 | 27.81 | 13.19 |
| 19.76 | 23.78 | 22.45 | 15.73 |
| 27.81 | 22.45 | 42.09 | 14.96 |
| 13.19 | 15.73 | 14.96 | 10.45 |
В матрице, (X T X) число 22, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X T и 1-го столбца матрицы X
Умножаем матрицы, (X T Y)
| 14.17 |
| 15.91 |
| 16.58 |
| 10.56 |
Находим определитель det(X T X) T = 34.35
Находим обратную матрицу (X T X) -1
| 0.6821 | 0.3795 | -0.2934 | -1.0118 |
| 0.3795 | 9.4402 | -0.133 | -14.4949 |
| -0.2934 | -0.133 | 0.1746 | 0.3204 |
| -1.0118 | -14.4949 | 0.3204 | 22.7272 |
Вектор оценок коэффициентов регрессии равен
s = (X T X) -1 X T Y =
| 0.1565 |
| 0.3375 |
| 0.0043 |
| 0.2986 |
Уравнение регрессии (оценка уравнения регрессии): Y = 0.1565 + 0.3375X 1+ 0.0043X 2+ 0.2986X 3
Матрица парных коэффициентов корреляции
Для y и x2
Уравнение имеет вид y = ax + b
Средние значения
Для y и x3
Уравнение имеет вид y = ax + b
Средние значения
Для x1 и x2
Уравнение имеет вид y = ax + b
Средние значения
Для x1 и x3
Уравнение имеет вид y = ax + b
Средние значения
Для x2 и x3
Уравнение имеет вид y = ax + b
Средние значения
Оценка среднеквадратичного отклонения равна
Частные коэффициент эластичности E1 2 = 0.62 2 = 0.38, т.е. в 38.0855 % случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — средняя
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл(n-m-1;a) = (18;0.05) = 1.734
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим
Интервальная оценка для коэффициента корреляции (доверительный интервал)
Доверительный интервал для коэффициента корреляции
r(0.3882;0.846)
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика
Статистическая значимость коэффициента регрессии b0не подтверждается
Статистическая значимость коэффициента регрессии b1не подтверждается
Статистическая значимость коэффициента регрессии b2не подтверждается
Статистическая значимость коэффициента регрессии b3не подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(bi— t iS i; bi+ t iS i)
b 0: (-0.7348;1.0478)
b 1: (-2.9781;3.6531)
b 2: (-0.4466;0.4553)
b 3: (-4.8459;5.4431)
Алгоритм вычисления коэффициента выборочной детерминации в MS-Excel Текст научной статьи по специальности « Математика»

- Математика
Аннотация научной статьи по математике, автор научной работы — Красильников Дмитрий Евгеньевич
Рассматривается коэффициент выборочной детерминации как критерий однородности выборок в социально-экономических исследованиях. Приводится геометрическое доказательство закона разложения дисперсии , предлагается алгоритм вычисления коэффициента выборочной детерминации в MS-Excel, рассматривается случай, когда закон разложения дисперсии не выполняется, показана связь между коэффициентом выборочной детерминации и эмпирическим корреляционным отношением .
Похожие темы научных работ по математике , автор научной работы — Красильников Дмитрий Евгеньевич
Текст научной работы на тему «Алгоритм вычисления коэффициента выборочной детерминации в MS-Excel»
Д. Е. Красильников
АЛГОРИТМ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА ВЫБОРОЧНОЙ ДЕТЕРМИНАЦИИ
Нижегородский почтамт. Отделение почтовой связи №24
Рассматривается коэффициент выборочной детерминации как критерий однородности выборок в социально-экономических исследованиях. Приводится геометрическое доказательство закона разложения дисперсии, предлагается алгоритм вычисления коэффициента выборочной детерминации в MS-Excel, рассматривается случай, когда закон разложения дисперсии не выполняется, показана связь между коэффициентом выборочной детерминации и эмпирическим корреляционным отношением.
Ключевые слова: коэффициент выборочной детерминации, закон разложения дисперсии, MS-Excel, критерий однородности выборок, дисперсионный анализ, эмпирическое корреляционное отношение.
При проведении социологических, психологических, экономических и маркетинговых исследований почти всегда встает вопрос о репрезентативности исследуемой выборки. Под репрезентативностью выборки, чаще всего, понимается ее однородность. При этом в современной литературе по соответствующим дисциплинам не дается универсальный метод проверки гипотезы об однородности. Как правило, для такой проверки используют так называемый ¿-критерий, F-критерий или критерий «Хи-квадрат» (см., например, [1]), которые базируются на сравнении средних величин со значением функции Стьюдента, Фишера или Хи -квадрат. Однако эти критерии слабо чувствительны к социально-экономическим данным ввиду небольшого разброса значений таких данных, а применение указанных функций недостаточно обосновано, так как эти критерии были разработаны для биологических, а не социально-экономических исследований.
Другим распространенным подходом к оценке репрезентативности является обоснованность выборки с позиций той или иной задачи. Например, при изучении спроса на автомобили стоимостью от миллиона рублей выборка, сделанная из лиц с доходом 8-10 тыс. руб. , будет всегда нерепрезентативной.
Тем не менее, в Советском Союзе была разработана специальная статистика (функция от выборочной совокупности), позволяющая оценить однородность любой выборки при условии ее стратификации — коэффициент выборочной детерминации (^2выб). Его не следует путать с коэффициентом детерминации (R2 ), который характеризует качество аппроксимации с помощью линейной функции и не имеет отношения к выборочному методу.
Данная статистика основана на разложении дисперсии на межгрупповую и внутриг-рупповую. Это разложение также используется в дисперсионном анализе. «Первоначально (1918 г.) дисперсионный анализ был разработан английским математиком-статистиком Р.А. Фишером для обработки результатов агрономических опытов по выявлению условий получения максимального урожая различных сортов сельскохозяйственных культур. Сам термин «дисперсионный анализ» Фишер употребил позднее [2, с. 392].
Чтобы понять, на чем основано разложение дисперсии, рассмотрим так называемый «прямоугольный выборочный план», используемый в однофакторном дисперсионном анализе (табл. 1).
Этот план представляет собой таблицу, в которой каждый столбец является выборкой с n элементами. Всего делается m таких выборок. В литературе эти столбцы часто называют факторами, группами или стратами, а само расположение элементов выборок — стратификацией.
© Красильников Д. Е., 2016.
В этой статье при обозначении элемента таблицы символом у, первый индекс указывает номер строки, а второй — номер столбца, в соответствии с правилом обозначения элементов матриц, принятым в Советском Союзе. Замечу, что в английской традиции принята обратная запись, то есть сначала пишут столбец, а затем строку, а в современной российской литературе встречаются оба варианта.
Очевидно, что общее число элементов в таблице N есть
Прямоугольный выборочный план
1 у11 у12 уЦ у 1т
2 у21 у22 у 2 i у 2т
1 у,1 у 2 у, у гт
п уп1 уп 2 у п] у пт
Среднее у1 у 2 у, у т
По каждому столбцу вычисляется среднее арифметическое у. (внутригрупповая средняя), которое заносится в последнюю строку таблицы,
Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
Глядя на любой набор данных распределенных во времени (динамический ряд), мы можем визуально определить падения и подъемы показателей, которые он содержит. Закономерность подъемов и падений называется трендом, который может говорить о том, увеличиваются или уменьшаются наши данные.
Пожалуй, цикл статей о прогнозировании я начну с самого простого — построении функции тренда. Для примера возьмем данные о продажах и построим модель, которая опишет зависимость продаж от времени.
Базовые понятия
Думаю, еще со школы все знакомы с линейной функцией, она как раз и лежит в основе тренда:
Y — это объем продаж, та переменная, которую мы будем объяснять временем и от которого она зависит, то есть Y(t);
t — номер периода (порядковый номер месяца), который объясняет план продаж Y;
a0 — это нулевой коэффициент регрессии, который показывает значение Y(t), при отсутствии влияния объясняющего фактора (t=0);
a1 — коэффициент регрессии, который показывает, на сколько исследуемый показатель продаж Y зависит от влияющего фактора t;
E — случайные возмущения, которые отражают влияния других неучтенных в модели факторов, кроме времени t.
Построение модели
Итак, мы знаем объем продаж за прошедшие 9 месяцев. Вот, что из себя представляет наша табличка:

Следующее, что мы должны сделать — это определить коэффициенты a0 и a1 для прогнозирования объема продаж за 10-ый месяц.
Определение коэффициентов модели
Строим график. По горизонтали видим отложенные месяцы, по вертикали объем продаж:
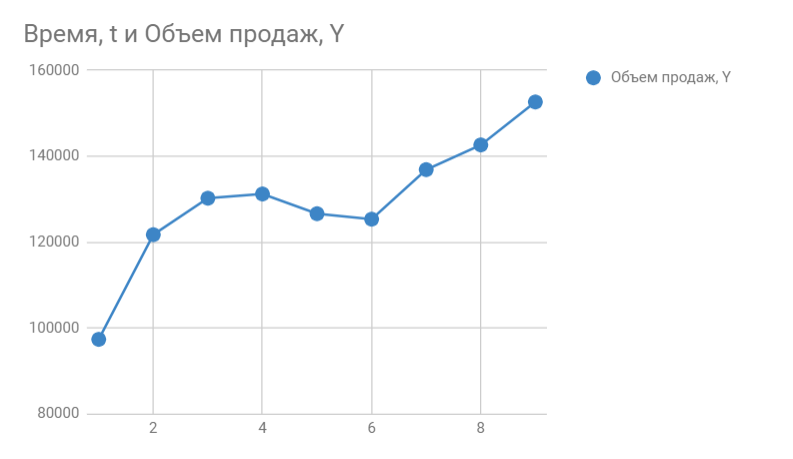
В Google Sheets выбираем Редактор диаграмм -> Дополнительные и ставим галочку возле Линии тренда. В настройках выбираем Ярлык — Уравнение и Показать R^2.
Если вы делаете все в MS Excel, то правой кнопкой мыши кликаем на график и в выпадающем меню выбираем «Добавить линию тренда».
По умолчанию строится линейная функция. Справа выбираем «Показывать уравнение на диаграмме» и «Величину достоверности аппроксимации R^2».
Вот, что получилось:
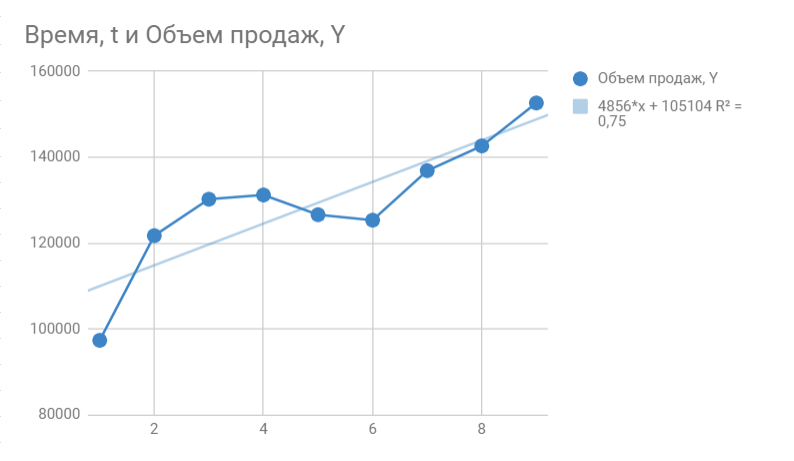
На графике мы видим уравнение функции:
y = 4856*x + 105104
Она описывает объем продаж в зависимости от номера месяца, на который мы хотим эти продажи спрогнозировать. Рядом видим коэффициент детерминации R^2, который говорит о качестве модели и на сколько хорошо она описывает наши продажи (Y). Чем ближе к 1, тем лучше.
У меня R^2 = 0,75. Это средний показатель, он говорит о том, что в модели не учтены какие-то другие значимые факторы помимо времени t, например, это может быть сезонность.
Прогнозируем
Чтобы рассчитать продажи за 10-ый месяц, подставляем в функцию тренда 10 вместо x. То есть,
y = 4856*10 + 105104
Получаем 153664 продажи в следующем месяце. Если добавим новую точку на график, то сразу видим, что R^2 улучшился.
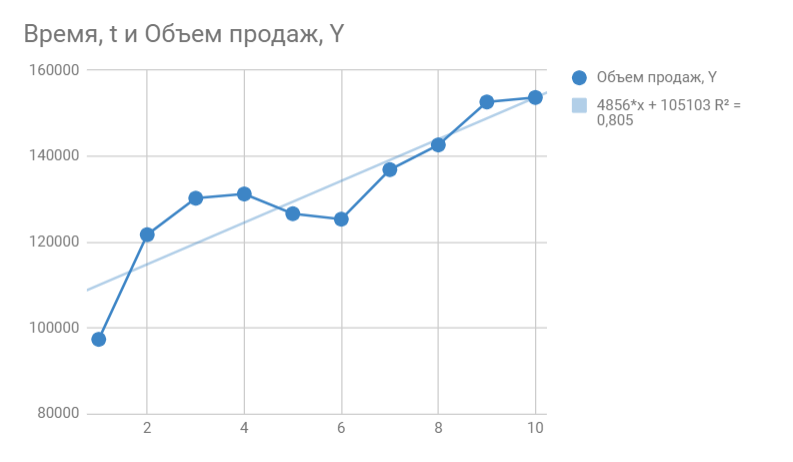
Таким образом вы можете спрогнозировать данные на несколько месяцев вперед, но без учета других факторов ваш прогноз будет лежать на линии тренда и будет не таким информативным как хотелось бы. К тому же, долгосрочный прогноз, сделанный таким способом будет очень приблизительным.
Повысить точность модели можно добавлением сезонности к функции тренда, что мы и сделаем в следующей статье.












