История науки и техники Com New

Арифметические операции над числами в компьютере

Если натуральные числа записаны в десятичной системе счисления, то мы пользуемся правилами сложения и вычитания чисел «столбиком». Действия сложения и вычитания целых многозначных чисел в -ичной системе счисления производятся по тем же правилам, что и в десятичной системе. В -ичной системе, как и в десятичной, при сложении многозначных чисел мы складываем сначала единицы, затем переходим к следующему разряду и т. д. до тех пор, пока не дойдем до самого старшего из имеющихся разрядов. При этом всякий раз, когда при сложении в предыдущем разряде получается сумма, большая, чем основание g системы счисления или равная ему, надо сделать перенос в следующий разряд.

Следующие примеры иллюстрируют операции сложения в шестиричной и двоичной системах счисления:

Вычитание в пятиричной системе иллюстрируется примером

Операция умножения целых многозначных чисел в -ичной системе счисления производится по тем же правилам, что и в десятичной системе («столбиком»). При выполнении операции умножения удобно пользоваться таблицами умножения. Ниже приведена таблица умножения в шестиричной системе. В каждой клетке этой таблицы стоит произведение чисел, представляющих номера строки и столбца, на пересечении которых находится клетка, причем все числа записаны в шестиричной системе счисления.

Следующий пример иллюстрирует операцию умножения («столбиком») в шестиричной системе:

История науки и техники Com New

Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.

Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 – 1 = 255 = 11111111и минимальное 0 = 00000000. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255.

В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536 = 0000001000011000будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536 = 1000001000011000 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 – 1 = 2 – 1 = 2 – 1 = 32767 = 111111111111111 и диапазон чисел будет находиться в пределах от -32767 до 32767.

Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.

Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:

1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;

2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);

3) к полученному обратному коду прибавить единицу к младшему разряду.

Например, для числа -536 в таком формате модуль будет равен 0000001000011000, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536, т. е. число 536, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.

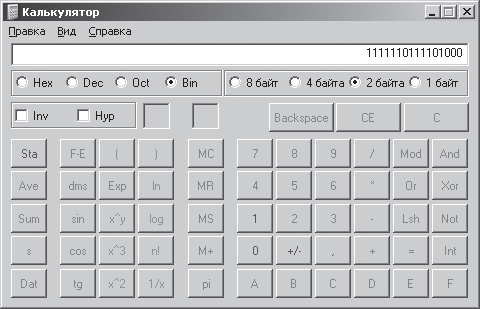
Рис. 2.6. Результат получения дополнительного кода

Необходимо помнить, что дополнительный код положительного числа – само число.

Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 – 1) … + 2 – 1 и -(2-1) … + 2 – 1.

Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).

Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.

Вычитание

Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:

В случае вычитания в текущем разряде из нуля единицы происходит заем из старшего разряда. По-сути мы вычитаем не из единицы, а из двоичного числа 10.

Арифметические действия в позиционных системах счисления

Рассмотрим арифметические действия в позиционных системах счисления на примере двоичной. Для этого удобно пользоваться таблицами сложения, вычитания, умножения и деления.

Умножим двоичные числа (11011) на (110). Умножение в двоичной системе счисления сводится к многократному сложению.

Арифметические операции в восьмеричной и шестнадцатеричной системах счисления выполняются аналогичным образом. Нужно построить соответствующие таблицы сложения, вычитания, умножения и деления. Но это весьма трудоёмкий процесс. Вычисления в этих системах счисления лучше доверить компьютеру.

Программистан
Бесплатные программы для вашего компьютера, полезные советы по Windows

Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

1. Сложение. Это действие состоит в том, что по нескольким числам, называемым слагаемыми , находится число, называемое их суммой .

Пример: 4+3=7, где 4 и 3 – слагаемые, а 7 – их сумма.

2. Вычитание – действие, посредством которого по данной сумме ( уменьшаемое ) и данному слагаемому ( вычитаемое ) находят искомое слагаемое ( разность ).
Это действие обратно сложению.

Пример: 7 – 3 = 4, где 7 – уменьшаемое, 3 – вычитаемое, а 4 – разность.

3. Умножение. Умножить некоторое число ( множимое ) на целое число ( множитель ) – значит повторить множимое слагаемым столько раз, сколько единиц содержится в множителе. Результат умножения называется произведением .

Пример: 2 ∙ 3 = 6, где 2 – множимое, 3 – множитель, а 6 – произведение. (2 ∙ 3 = 2 + 2+ 2 = 6)

Если множитель и множимое меняются ролями, то произведение остается тем же. Поэтому множитель и множимое также называются сомножителями.

Пример: 2 ∙ 3 = 3 ∙ 2, то есть (2 + 2 + 2 = 3 + 3)

Полагают, что если множителем является 1, то a ∙ 1 = a.

Например: 2 ∙ 1 = 2, 44 ∙ 1 = 44, 13 ∙ 1 = 13.

4. Деление. Посредством деления по данному произведению ( делимое ) и данному сомножителю ( делитель ) находят искомый сомножитель ( частное ).
Это действие обратно умножению.

Пример: 8 : 2 = 4, где 8 – делимое, 2 – делитель, а 4 – частное.

Проверка деления: произведение делителя 2 и частного 4 дает делимое 8. 2 ∙ 4 = 8

Деление с остатком

Если при делении целого числа на целое число в частном получается целое число, то такое деление целых чисел называется точным, или, что первое число нацело делится (или просто – делится) на второе.

Например: 35 делится (нацело) на 5, частное есть целое число 7.

Второе число при этом называется делителем первого, первое же – кратным второго.

Во многих случаях можно, не выполняя деления, узнать, делится ли нацело одно целое число на другое (см. признаки делимости).

Точное деление возможно далеко не всегда. В таком случае выполняют так называемое деление с остатком. В этом случае находят такое наибольшее число, которое при умножении на делитель даст произведение, не превосходящее делимого. Это число называется неполным частным . Разность между делимым и произведением делителя на неполное частное называется остатком от деления .
Делимое равно делителю, умноженное на неполное частное, плюс остаток. Остаток всегда меньше делителя.

Пример: Неполное частное от деления числа 27 на 4 равно 6, а остаток равен 3. Очевидно, 27 = 4∙6 + 3 и 3˂4.

5. Возведение в степень. Возвести некоторое число в целую степень (во вторую, в третью и т.д.) – значит взять это число сомножителем два, три раза и т.д. Иначе говоря, возведение в степень выполняется повторным умножением.
Число, которое берётся сомножителем, называется основанием степени ; число, показывающее, сколько раз повторяется основание, называется показателем степени ; результат возведения числа в степень называется степенью этого числа.

Пример: 2∙2∙2 = 2³ = 8; где 2 – основание степени, 3 – показатель степени, 8 – степень.

Вторую степень числа иначе называют квадратом, третью степень – кубом. Первой степенью числа называют само это число.

6. Извлечение корня есть действие, посредством которого по данной степени ( подкоренное число ) и данному показателю степени ( показатель корня ) находят искомое основание ( корень ).
Это действие обратно возведению в степень.

Пример: ³√64 = 4; где 64 – подкоренное число, 3 – показатель корня, 4 – корень.

Проверка извлечения корня: 4³=64. Возведение числа 4 в 3-ю степень даёт 64.

Корень второй степени иначе называют квадратным; корень третьей степени – кубическим.
При знаке квадратного корня показатель корня принято опускать: √36 = 6 означает ²√36 = 6.

Использованная лит-ра:
Справочник по элементарной математике — Выгодский М.Я., «Наука», 1974 г.
Справочник по математике. Пособие для учащихся 9—11 кл. — Шахно К. У., «Учпедгиз», 1961 г.

При полной или частичной публикации статьи в Интернете обязательно указание активной гиперссылки на источник http://programmistan.narod.ru

Необходимая Арифметика: Арифметические действия над числами: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Длинная арифметика. Сложение, вычитание, умножение на короткое/длинное число

Числа, для представления которых в стандартных типах данных не хватает количества разрядов, называются длинными. Реализация арифметических операций над такими «длинными» числами называется длинной арифметикой. Задачи на «длинную» арифметику возникают, когда разрядности стандартных типов данных (целые, длинные целые, вещественные числа) не хватает чтобы хранить результат (настолько он велик).

Например, вычислить 30! (30 факториал) = 265252859812191058636308480000000, это число больше чем, например, максимальное для типа int64 — 9223372036854775807. В этом случае используется прием хранения длинных чисел в виде строки или массива цифр, а чтобы выполнять арифметические действия с такими числами, необходимо написать специальные процедуры сложения, умножения и деления длинных чисел, которые основаны на правилах вычисления «в столбик».

Итак Длинная арифметика — набор структур данных и алгоритмов, которые позволяют работать с числами гораздо большими, чем это позволяют стандартные типы данных.

Длинная арифметика используется:

• При решении олимпиадных задач.
• В компьютерах низкой разрядности, микроконтроллерах (например, процессор умеет работать только с числами длиной 8 бит, 8 двоичных разрядов, в 8 битах можно представить только числа от 0 до $2^8-1=255$, а требуется обрабатывать большие числа).
• Криптография.
• Математическое и финансовое ПО, требующее, чтобы результат вычисления на компьютере совпал до последнего разряда с результатом вычисления на бумаге. В частности, калькулятор Windows (начиная с 95)
• «Спортивные» вычисления знаменитых трансцендентных чисел («число Пи», «число e» и т. д.) с высокой точностью. Вещественное число — число, которое может возникать как результат измерения (Например: 4,31; 5,23432; корень из 2-х). Множество вещественных чисел больше чем множество рациональных дробей (чисел представляющихся в виде дроби), но меньше чем множество комплексных чисел. Комплексное число — расширение множества вещественных чисел за счёт добавления мнимой компоненты числа. Комплексное число представляется в виде: x+iy, где x и y — вещественные числа, а i-мнимая единица.
• Высококачественные изображения фракталов.

Представление в компьютере длинных чисел

Реализация операций с длинными числами во многом определяется тем, как представить их в памяти компьютера. «Длинное» число можно записать, например, с помощью массива десятичных цифр, количество элементов в таком массиве равно количеству значащих цифр в «длинном» числе. При этом размер массива должен быть достаточным, чтобы разместить в нем и результат, например, умножения.

Классификация реализации длинной арифметики (преимущества и недостатки различных способов) Количество знаков может быть фиксированным (знаки хранятся в массиве с индексом от 0 до количества знаков минус 1) и с переменной длиной (отдельно ещё хравнится длина числа).

Количество цифр	Только целые числа	Действительные числа
Фиксированное	«+» Простота реализации
Переменное	«+» Экономия памяти

Разряды в позиционной системе счисления.

Рассмотрим реализацию операций в простейшем случае — с целыми положительными числами

Существуют и другие представления «длинных» чисел. Рассмотрим одно из них. Представим наше число
30! = 265252859812191058636308480000000 в виде: 30! = 2 * (10 4 ) 8 + 6525 * (10 4 ) 7 + 2859 * (10 4 ) 6 + 8121 * (10 4 ) 5 + 9105 * (10 4 ) 4 + 8636 * (10 4 ) 3 + 3084 * (10 4 ) 2 + 8000 * (10 4 ) 1 + 0000 * (10 4 ) 0 .

Для вычислений его удобно хранить в виде массива:

Номер элемента в массиве А	0	1	2	3	4	5	6	7	8	9
Значение	9	0000	8000	3084	8636	9105	8121	2859	6525	2

Наше «длинное» число представлено в 10000-10 системе счисления (десятитысячно-десятичная система счисления, приведите аналогию с восьмерично-десятичной системой счисления), а «цифрами» числа являются четырехзначные числа. 9 в А [0] — длина числа. Число хранится «задом наперед», начиная с младшего разряда.

Алгоритмы чтения и записи длинных чисел

Ввод длинного числа из файла. Решение задачи начнем с описания данных.

При обработке каждой очередной цифры входного числа старшая цифра элемента массива с номером i становится младшей цифрой числа в элементе i + 1, а вводимая цифра будет младшей цифрой числа из А[1]. В результате работы нашего алгоритма мы получили число, записанное «задом наперед».

Задачи на длинную арифметику

Задача 1. (Районная олимпиада 1997).
Числа Фибоначчи выписываются подряд, начиная с Ф(1). Какая цифра будет на N-ом месте (N < 5000)?

Указание: Ф(n+1) = Ф(n) + Ф(n-1); Ф(1) = Ф(2) = 1

Необходимо написать процедуру сложения «длинных» чисел (представленных в виде массивов отдельных разрядов A и B). В первой ячейке массива будем хранить «длину» числа (количество разрядов). Массив B содержит предыдущее вычисленное число Фибоначчи, а массив A – текущее число. Для удобства сложения полагаем Ф(0) = 0.

Программа на Basic для сложения 2 «длинных чисел» :

Реализация знаковой длинной целой арифметики для Delphi: cложение, вычитание, умножение и деление.