Вещественные числа в памяти компьютера
Вещественные числа в памяти компьютера представляются в форме с плавающей точкой.
Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:
R = m * (р^n) Например, число 25,324 можно записать в таком виде: 0.25324х102. Здесь m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».
Однако справедливы и следующие равенства:
25,324 = 2,5324*(10^1) = 0,0025324*(10^4) = 0,25324*(10^2) и т.п. Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализован-ном представлении должна удовлетворять условию:
± машинный порядок М А Н Т И С С А
В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы.
Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:
Машинный порядок 0 1 2 3 . 64 65 . 125 126 127 Математический порядок -64 -63 -62 -61 . 0 1 . 61 62 63 Если обозначить машинный порядок Мр, а математический — р, то связь между ними ыразится такой формулой:
Мр = р + 64. Итак, машинный порядок смещен относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает.
Полученная формула записана в десятичной системе. Поскольку 6410=4016 (проверьте!), то в шестнадцатеричной системе формула примет вид:
Мр16 = р16 + 4016 И, наконец, в двоичной системе:
Мр2 = р2+100 00002 Теперь мы можем записать внутреннее представление числа 25,324 в форме с плавающей точкой. Переведем его в двоичную систему счисления с 24 значащими цифрами. 25,32410= 11001,01010010111100011012 Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,110010101001011110001101*10101 Здесь мантисса, основание системы счисления (210=102) и порядок (510=1012)записаны в двоичной системе. Вычислим машинный порядок. Мр2 = 101 + 100 0000 = 100 0101 Запишем представление числа в ячейке памяти. 01000101 11001010 10010111 10001101 Это и есть искомый результат. Его можно переписать в более компактной шестнадцатеричной форме:
45 CA 97 8D Для того, чтобы получить внутреннее представление отрицательного числа -25,324,достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.
11000101 11001010 10010111 10001101 А в шестнадцатеричной форме:
C5 CA 97 8D Никакого инвертирования, как для отрицательных чисел с фиксированной точкой, здесь не происходит.
Рассмотрим, наконец, вопрос о диапазоне чисел, представимых в форме с плавающей точкой. Очевидно, положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим порядком:
0,111111111111111111111111*1021111111 Если перевести в десятичную систему, то получится
Rmax = (1 — 2-24) * 264 = 1019 Очевидно, что диапазон вещественных чисел значительно шире диапазона целых чисел. Если в результате вычислений получается число по модулю большее, чем Rmax, то происходит прерывание работы процессора. Такая ситуация называется переполнением при вычислениях с плавающей точкой. Наименьшее по модулю ненулевое значение равно:
(1/2) * 2-64=2-66. Любые значения, меньшие данного по абсолютной величине, воспринимаются процессором как нулевые.
Как известно из математики, множество действительных чисел бесконечно и непрерывно. Множество же вещественных чисел, представимых в памяти ЭВМ в форме с плавающей точкой, является ограниченным и дискретным. Каждое следующее значение получается прибавлением к мантиссе предыдущего единицы в последнем (24-м) разряде. Количество вещественных чисел, точно представимых в па-мяти машины, вычисляется по формуле:
N = 2t * ( U — L+ 1) + 1. Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, L = -64) получается:
N = 2 146 683 548. Все же остальные числа, не попадающие в это множество, но находящиеся в диапазоне допустимых значений, представляются в памяти приближенно (мантисса обрезается на 24-м разряде). А поскольку числа имеют погрешности, то и результаты вычислений с этими числами также будут содержать погрешность. Из сказанного следует вывод: вычисления с вещественными числами в компьютере выполняются приближенно.
ДРОБНЫЕ ЧИСЛА В ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ
В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.
Запишем формулу представления дробного числа в позиционной системе счисления:
Ap = an-1·p n-1 +an-2·p n-2 + . + a1·p 1 +a0·p 0 +a-1·p -1 +a-2·p -2 + . + a-m·p -m , [4.1]
В случае десятичной системы счисления получим:
Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.116 • 2 = 0.232 .232 • 2 = 0.464 .464 • 2 = 0.928 .928 • 2 = 1.856 .856 • 2 = 1.712 .712 • 2 = 1.424 .424 • 2 = 0.848 .848 • 2 = 1.696 .696 • 2 = 1.392 .784 • 2 = 0.784 и т.д.
Получим: 20610=11001110,00011101102
Таблицу степеней первых восьми отрицательных степеней двойки можно посмотреть в Приложении.
История науки и техники Com New
Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.
Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 – 1 = 255 = 11111111и минимальное 0 = 00000000. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255.
В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536 = 0000001000011000будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536 = 1000001000011000 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 – 1 = 2 – 1 = 2 – 1 = 32767 = 111111111111111 и диапазон чисел будет находиться в пределах от -32767 до 32767.
Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.
Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:
1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;
2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);
3) к полученному обратному коду прибавить единицу к младшему разряду.
Например, для числа -536 в таком формате модуль будет равен 0000001000011000, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536, т. е. число 536, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.
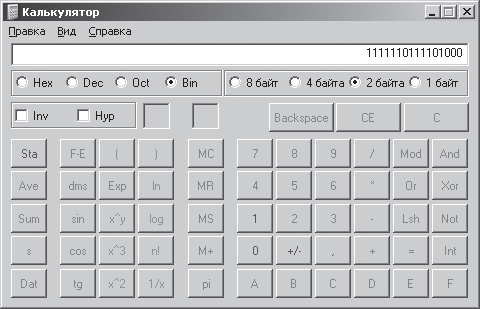
Рис. 2.6. Результат получения дополнительного кода
Необходимо помнить, что дополнительный код положительного числа – само число.
Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 – 1) … + 2 – 1 и -(2-1) … + 2 – 1.
Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).
Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.
Представление дробных чисел в компьютере
Представление чисел в формате с фиксированной запятой. Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «запятая» «находится» справа после младшего разряда, то есть вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А2 = = 111100002 будет храниться в ячейке памяти следующим образом:
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно
А = 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 = 1 × 2 8 — 1 = 25510.
Диапазон изменения целых неотрицательных чисел чисел: от 0 до 255.
Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1).
Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа. Например, число 200210 = 111110100102 будет представлено в 16-разрядном представлении следующим образом:
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно:
Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.
Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2 n — |A|.
Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, так как в n-разрядной компьютерной арифметике:
поскольку в компьютерной n-разрядной арифметике 2 n = 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, то есть n нулей.
Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:
1. Модуль числа записать в прямом коде в n двоичных разрядах.
2. Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).
3. К полученному обратному коду прибавить единицу.
Запишем дополнительный код отрицательного числа -2002 для 16-разрядного компьютерного представления:
При n-разрядном представлении отрицательного числа А в дополнительным коде старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число
Чтобы число было положительным, должно выполняться условие
Следовательно, максимальное значение модуля числа А в га-разрядном представлении равно:
Тогда минимальное отрицательное число равно:
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится четыре ячейки памяти — 32 бита).
Максимальное положительное целое число (с учетом выделения одного разряда на знак) равно:
А = 2 31 — 1 = 2 147 483 64710.
Минимальное отрицательное целое число равно:
А = -2 31 = — 2 147 483 64810.
Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций.
Недостатком представления чисел в формате с фиксированной запятой является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.
Представление чисел в формате с плавающей запятой. Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. В этом случае положение запятой в записи числа может изменяться.
Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так число А может быть представлено в виде:
| A = m × q n | 2.3 |
где m — мантисса числа;
q — основание системы счисления;
n — порядок числа.
Для единообразия представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:
Здесь нормализованная мантисса: m = 0,55555, порядок: n = 3.
Число в формате с плавающей запятой занимает в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности). При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы.
Определим максимальное число и его точность для формата чисел обычной точности, если для хранения порядка и его знака отводится 8 разрядов, а для хранения мантиссы и ее знака — 24 разряда:
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| знак и порядок | знак и мантисса | ||||||||||||||||||||||
Максимальное значение порядка числа составит 11111112 = 12710, и, следовательно, максимальное значение числа составит:
2 127 = 1,7014118346046923173168730371588 × 10 38 .
Максимальное значение положительной мантиссы равно:
2 23 — 1 » 2 23 = 2 (10 × 2,3) » 1000 2,3 = 10 (3 × 2,3) » 10 7 .
Таким образом максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411 × 10 38 (количество значащих цифр десятичного числа в данном случае ограничено 7 разрядами).
1.26. Заполнить таблицу, записав отрицательные десятичные числа в прямом, обратном и дополнительном кодах в 16-разрядном представлении:
| Десятичные числа | Прямой код | Обратный код | Дополнительный код |
| -50 | |||
| -500 |
1.27. Определить диапазон представления целых чисел со знаком (отводится 2 байта памяти) в формате с фиксированной запятой.
1.28. Определить максимальное число и его точность для формата чисел двойной точности, если для хранения порядка и его знака отводится 11 разрядов, а для хранения мантиссы и ее знака — 53 разряда.
Вариант 1
1. Если число отрицательное, то в знаковый разряд помещается
2. Числом в нормальной форме с нормализованной мантиссой (правильной дробью, имеющей после запятой цифру, отличную от нуля) является
1) 7815
2) 2783,00029
3) 0,03428
4) 0,401 x 10 7
3. Беззнаковым 8-разрядным представлением числа 4510 является
1) 00101101
2) 101101
3) 10110100
4) 00000101
4. Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?
5. При записи числа в форме A = ± m x q p , где q — это
1) мантисса
2) само вещественное число
3) порядок числа
4) основание системы счисления
6. Укажите десятичный эквивалент числа, прямой код которого 00010101 записан в 8-разрядном формате со знаком
1) 21
2) 34
3) -21
4) верного ответа в предложенных вариантах нет
7. Укажите число, записанное в естественной форме
1) 2010,0102
2) 1,784824E+5
3) 95400611 x 10 2
4) среди предложенных вариантов нет числа в естественной форме
Ответы на тест по информатике Представление чисел в компьютере для 8 класса
Вариант 1
1-4
2-1
3-4
4-14
5-3
6-2
7-3
Вариант 2
1-2
2-4
3-1
4-23
5-4
6-1
7-1