Арифметические и логические (битовые) операции. Маски

Что сперва умножение или деление

Вы уди­ви­тесь, но боль­шин­ство людей не смо­гут пра­виль­но это посчи­тать. Посчи­тай­те сами и потом смот­ри­те пра­виль­ный ответ:

В интер­не­те мно­го спо­ров про такие при­ме­ры, поэто­му мы реши­ли разо­брать­ся, какие ошиб­ки совер­ша­ют чаще все­го и поче­му мно­гие счи­та­ют непра­виль­но. Для реше­ния нам пона­до­бят­ся три мате­ма­ти­че­ских пра­ви­ла:

1. То, что в скоб­ках, выпол­ня­ет­ся в первую оче­редь. Если ско­бок несколь­ко, они выпол­ня­ют­ся сле­ва напра­во.
2. При отсут­ствии ско­бок мате­ма­ти­че­ские дей­ствия выпол­ня­ют­ся сле­ва напра­во, сна­ча­ла умно­же­ние и деле­ние, потом — сло­же­ние и вычи­та­ние.
3. Меж­ду мно­жи­те­лем и скоб­кой (или дву­мя скоб­ка­ми) может опус­кать­ся знак умно­же­ния.

Раз­бе­рём подроб­нее, что это зна­чит в нашем слу­чае.

1. То, что в скоб­ках, выпол­ня­ет­ся в первую оче­редь. То есть в нашем при­ме­ре, вне зави­си­мо­сти от чего угод­но, сна­ча­ла схлоп­нут­ся скоб­ки:

8 / 2(2 + 2) → 8 / 2(4)

2. Меж­ду чис­лом и скоб­кой мож­но опу­стить знак умно­же­ния. У нас перед скоб­кой двой­ка, то есть мож­но сде­лать такую заме­ну:

3. Мате­ма­ти­че­ские дей­ствия при отсут­ствии ско­бок выпол­ня­ют­ся сле­ва напра­во: как при чте­нии, сна­ча­ла умно­же­ние и деле­ние, потом — сло­же­ние и вычи­та­ние. Умно­же­ние и деле­ние име­ют оди­на­ко­вый при­о­ри­тет. Нет тако­го, что сна­ча­ла все­гда дела­ет­ся умно­же­ние, затем деле­ние, или наобо­рот. Со сло­же­ни­ем и вычи­та­ни­ем то же самое.

Неко­то­рые счи­та­ют, что раз мно­жи­те­ли были напи­са­ны близ­ко друг к дру­гу (когда там сто­я­ли скоб­ки), то оно выпол­ня­ет­ся в первую оче­редь, ссы­ла­ясь при этом на раз­ные мето­ди­че­ские посо­бия. На самом деле это не так, и нет тако­го скры­то­го умно­же­ния, кото­рое име­ет при­о­ри­тет над дру­гим умно­же­ни­ем или деле­ни­ем. Это такое же умно­же­ние, как и осталь­ные, и оно дела­ет­ся в общем поряд­ке — как и при­ня­то во всём мате­ма­ти­че­ском мире.

Полу­ча­ет­ся, что нам сна­ча­ла надо сло­жить 2 + 2 в скоб­ках, потом 8 раз­де­лить на 2, и полу­чен­ный резуль­тат умно­жить на то, что в скоб­ках:

8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16

Кста­ти, если на айфоне запи­сать это выра­же­ние точ­но так же, как в усло­вии, теле­фон тоже даст пра­виль­ный ответ.

А инже­нер­ный каль­ку­ля­тор на Windows 10 так запи­сы­вать не уме­ет и про­пус­ка­ет первую двойку-множитель. Попро­буй­те сами 🙂

Тут в тред вры­ва­ют­ся мате­ма­ти­ки и с воп­ля­ми «Шустеф!» пояс­ня­ют кри­ком:

«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исклю­че­ние: в алгеб­ре знак умно­же­ния свя­зы­ва­ет ком­по­нен­ты дей­ствия силь­нее, чем знак деле­ния, поэто­му знак умно­же­ния опус­ка­ет­ся. Напри­мер, a:b·c= a: (b·c)».

Этот текст из «Мето­ди­ки пре­по­да­ва­ния алгеб­ры», курс лек­ций, Шустеф М. Ф., 1967 год. (стр. 43)

Раз в спор­ном при­ме­ре знак умно­же­ния опу­щен, то спор­ный при­мер алгеб­ра­и­че­ский, а зна­чит, сна­ча­ла умно­жа­ем 2 на 4, а потом 8 делим на 8!

А вот как на это отве­ча­ют те, кто дей­стви­тель­но в теме и не ленит­ся пол­но­стью посмот­реть пер­во­ис­точ­ник:

«Для устра­не­ния недо­ра­зу­ме­ний В. Л. Гон­ча­ров ука­зы­ва­ет, что пред­по­чти­тель­нее поль­зо­вать­ся в каче­стве зна­ка деле­ния чер­той и ста­вить скоб­ки [87]. П. С. Алек­сан­дров и А. Н. Кол­мо­го­ров [59] пред­ло­жи­ли изме­нить поря­док дей­ствий в ариф­ме­ти­ке и решать, напри­мер, так: 80:20×2=80:40=2 вме­сто обыч­но­го: 80:20×2=4×2=8. Одна­ко это пред­ло­же­ние не нашло под­держ­ки».

Если апел­ли­ро­вать к Фри­де Мак­совне Шустеф, то выхо­дит, что:

1. В. Л. Гон­ча­ров гово­рит так: «Ребя­та, исполь­зуй­те чер­ту и ставь­те скоб­ки, что­бы ни у кого не было вопро­сов про при­о­ри­тет».
2. Если у нас всё же бит­ва ариф­ме­ти­ки и алгеб­ры, то, по П. С. Алек­сан­дро­ву и А. Н. Кол­мо­го­ро­ву, при­мер нуж­но решать сле­ва напра­во, как обыч­но. Они, конеч­но, пред­ло­жи­ли решать такое по-другому, но науч­ное сооб­ще­ство их не под­дер­жа­ло.

Самое инте­рес­ное, что даль­ше в при­ме­рах Фри­да Мак­сов­на поль­зу­ет­ся как раз пра­виль­ным поряд­ком дей­ствий, объ­яс­няя реше­ние. Даже там, где есть умно­же­ние на скоб­ку с опу­щен­ным зна­ком, она выпол­ня­ет дей­ствия сле­ва напра­во.

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

Сложение в обратных кодах

Случай 1. $A$ и $B$ — положительные числа.

При сложении таких чисел просто суммируются их обратные коды (для положительных чисел они равны прямым), включая знаковый разряд. Т.к. знаковый разряд у положительных чисел равен

Сложение в дополнительных кодах

Случай $1$. $A$ и $B$ — положительные.

Стандартный случай, т.к. у положительных чисел прямой, обратный и дополнительный коды совпадают.

Случай $2$. $A$ — положительное, $B$ — отрицательное, по модулю больше $A$.

В случае использования дополнительных кодов получим сразу правильный результат, в отличие от сложения обратных кодов.

Случай $3$. $A$ — положительное, $B$ — отрицательное, по модулю меньше $A$.

В отличие от сложения обратных кодов, где нужно было прибавлять «лишнюю» единицу к полученному коду, в этом случае нужно ее просто отбросить.

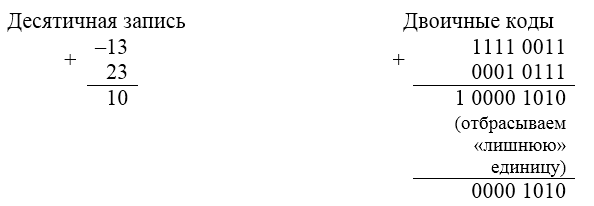
Случай $4$. $A$ и $B$ — отрицательные.

В этом случае тоже отбрасываем «лишнюю» единицу.

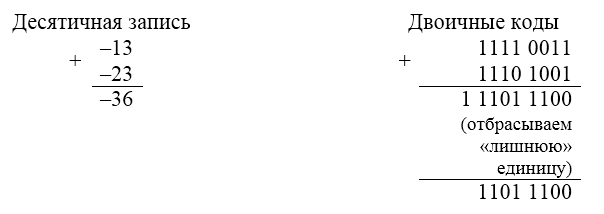
Случай $5$ и $6$. Переполнение — аналогично обратному.

При необходимости выполнения вычитания чисел, оно сводится к сложению отрицательных чисел. Например, $A-B=A+(-B).$

$, то у суммы он также равен

Умножение

Т.к. умножение — сложная операция, то специально для нее в компьютере имеется регистр (накапливающий сумматор) и с помощью последовательности сдвигов и сложений получается результат.

Умножение в двоичной системе выполняется быстрее, чем сложение и вычитание, т.к. сложение можно производить в прямом коде.

Для определения знака результата умножения над знаковыми разрядами совершается операция сложения по модулю («строгое (исключающее) ИЛИ» или «XOR»).

Умножим числа $-13$ и $23$:

Для удобства умножения нули между знаковым разрядом и первой цифрой числа за писывать не будем.

Полученный результат содержит $10$ цифр. Приведем его к виду из $16$ бит, добавив нули между знаковым разрядом и модулем числа:

$1000 0001 0010 1011.$

$, таким образом, число также будет положительным.

Случай 2. $A$ — положительное, $B$ — отрицательное, по модулю больше $A$.

В этом случае числа $A$ и $B$ (для отрицательного числа берется обратный код) просто складываются и получается результат в обратном коде:

Для перевода результата в прямой код биты цифровой части инвертируются: $1000 1010=-10$.

Случай 3. $A$ — положительное, $B$ — отрицательное, по модулю меньше $A.$

Если в этом случае поступить таким же образом, то получим ошибку расчета. Компьютер решает эту проблему переносом получившейся «лишней единицы» из знакового разряда в младший разряд получившейся суммы. Не забываем для отрицательного числа $A$ записать обратный код:

Готовые работы на аналогичную тему

Случай 4. $A$ и $B$ — отрицательные.

В этом случае во избежание ошибки снова нужно будет перенести единицу из знакового разряда в младший разряд числа.

При сложении чисел возможен вариант переполнения, когда полученный результат не помещается в выделенное для него место в памяти.

Самый надежный способ проверки не произошло ли переполнение — проверка знака результата. Если он получается не таким, какой должен быть, значит произошло переполнение.

Максимально возможное значение по модулю для чисел со знаком равно $2^$, где n — количество бит для хранения числа.

Например, если на хранение числа отводится $1$ байт, то максимально возможное значение по модулю $2^=2^7=128$. Если число по модулю получается больше, то для операции необходимо выделить больше памяти.

Заметим, что переполнение возможно в случае, когда числа имеют одинаковый знак (оба положительны или оба отрицательны).

Случай 5. Переполнение, когда $A$ и $B$ — положительные.

Мы получили в результате сложения двух положительных чисел — отрицательное. Т.е. произошло переполнение. Ситуация решается расширением диапазона:

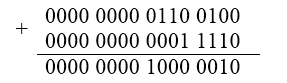
Случай 6. Переполнение, когда $A$ и $B$ — отрицательные.

Ситуация такая же, как и в случае $5$. Решается тем же способом — расширением диапазона.

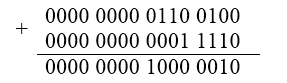
Статьи к прочтению:

Для того, чтобы вычисть числа в системе счисления с основанием q, необходимо записать одно под другим столбиком, чтобы разряды вычитаемого располагались…

Тема 3. ПРЕДОСТАВЛЕНИЕ ЧИСЕЛ В КОМПЬЮТЕРЕ Вопросы: 1. Компьютерное представление целых и вещественных чисел. 2. Арифметика двоичных чисел 2.1. Сложение в…

Арифметические операции

Арифметические операции + – сложение— – вычитание* – умножение/ – делениеDIV – деление нацелоMOD – остаток от деления

Арифметические операции Унарные операции – применяются к одной переменной.++ – увеличение на единицу (x++ выдаёт старое значение, ++x – новое значение).– – – уменьшение на единицу, аналогично операции ++.Бинарные операции – стоят между двумя переменными или

Сложение двоичных чисел

Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.

Пример : 1011,1₂ + 1010,11₂

Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример : 111,1₂ + 111₂ + 101,1₂

При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 100₂. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 101₂. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.

Умножение

При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.

Пример 3. Выполнить умножение двоичных нормализованных чисел:

(0.11101·2 101 )·(0.1001·2 11 ) = (0.11101·0.1001)· 2 (101+11) = 0.100000101·2 1000 .

Excel как калькулятор

Таблицу Excel можно использовать элементарно как обычный калькулятор. Если возникнет необходимость отдельно от таблицы с данными произвести какие-то промежуточные вычисления, нам теперь не нужно отвлекаться и использовать отдельное приложение калькулятора, всё делается у нас в любой пустой ячейке Microsoft Excel. Ставим знак «=». Вводим нужное арифметическое вычисление – сложение, вычитание, умножение, деление, возведение в степень. Жмём Enter и получаем результат.

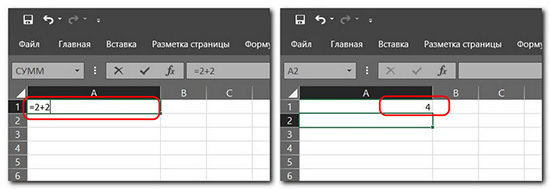
Можем произвести более сложное вычисление.

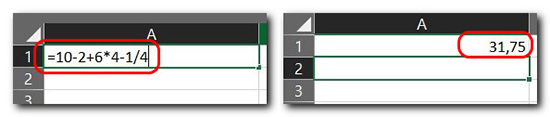
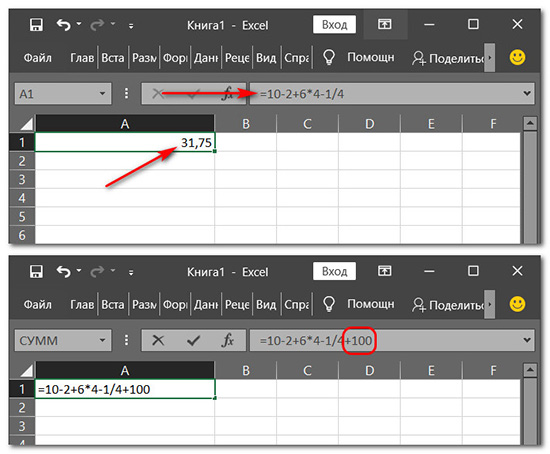
Если вычисление нужно скорректировать или доработать, тогда кликаем ячейку с результатом. Делаем клик в строке формул Excel, изменяем или довычисляем что нужно. Жмём Enter.

Простейшие операции над 32-битными числами

Сразу возникает вопрос: если регистры у нас 16-битные, то как с их помощью обрабатывать 32-битные числа? Ответ очевиден: мы просто будем задавать каждое число не одним регистром, а сразу двумя.

Только нам надо сначала определиться, какими регистрами и как мы будем для этого пользоваться. Давай не станем изобретать велосипед, а поищем подсказки в самом процессоре 8088.

У 8088 есть инструкция mul , которая умножает AX на 16-битный регистр и кладет результат в DX:AX . Также у него есть инструкция div , которая делит DX:AX на 16-битный регистр; результат попадает в регистр AX , а остаток — в DX . Еще у 8088 есть инструкция cwd . Она конвертирует знаковое 16-битное число из регистра AX в 32-битное число DX:AX .

Давай и мы, по примеру этих трех инструкций, тоже будем хранить 32-битные числа в DX:AX (в DX старшее слово, в AX — младшее). Но чтобы выполнять арифметические операции, нам нужно еще одно 32-битное число. Его, по аналогии с первым, будем хранить в CX:BX (в CX старшее слово, в BX — младшее).

Ну вот, мы с тобой условились, где и как хранить 32-битные числа. Теперь давай реализуем для них операцию сложения и операцию вычитания. Для этого нам пригодятся инструкции adc и sbb . Вот так выглядит сложение.

Удивлен, что операция сложения у нас заняла всего две инструкции? Сейчас объясню, что тут происходит. Дело в том, что, когда ты выполняешь инструкцию add , она не только складывает два числа, но и изменяет флаг переноса. Когда результат операции сложения не умещается в сдвоенный байт, инструкция add помещает старшую цифру результата (это всегда единица) во флаг переноса.

Инструкция adc dx, cx выполняет вот такую операцию: DX = DX + CX + перенос , то есть прибавляет к итоговому результату то значение, которое хранится во флаге переноса.

Теперь давай реализуем вычитание 32-битных чисел по такому же принципу.

Что тут происходит? Инструкция sub вычитает из одного числа другое, а еще изменяет флаг переноса. Когда операция вычитания делает «заем» из соседнего разряда, флаг переноса устанавливается в единицу.

Инструкция sbb dx, cx выполняет вот такую операцию: DX = DX – CX – перенос , то есть вычитает из итогового результата то значение, которое хранится во флаге переноса.

Мы с тобой успешно реализовали операции сложения и вычитания. Теперь давай реализуем логическое инвертирование и арифметическое инвертирование.

Чтобы сделать логическое инвертирование 32-битного числа ( not ), нам надо просто переключить все биты числа на противоположные.

Если требуется выполнить арифметическое инвертирование ( neg ), то есть поменять знак числа, нужно сделать то же самое, но только прибавить единицу к результату.

«Совсем вишня»

В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.

От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.