Внутреннее представление вещественных чисел в памяти компьютера

ГДЗ Информатика 10 класс Семакин §5 Представление чисел в компьютере

Дискретное счётное множество представляет собой любое конечное множество, которое и так по определению дискретно. Ограничено оно потому, память и так сама по себе квантирована и не бесконечна. Можно представить память неограниченной. Но адресное пространство не может быть большим до бесконечности. То есть компьютер работает только с ограниченной разрядной сеткой.

2. Определите диапазон целых чисел, хранящихся в 1 байте памяти в двух вариантах: со знаком и без знака.

1 байт это 8 бит соответственно в нем может хранится 2^8 = 256 значений

если в нем хранить числа без знака, то мы сможем записать 256 неотрицательных чисел это числа от 0 до 255

если же со знаком, то тогда половина диапазона будет отрицательным, а половина неотрицательным поэтому будет 256 / 2 = 128 отрицательных чисел и столько же неотрицательных поэтому получится диапазон от -128 до 127

3. Получите внутреннее представление числа 157 в 8-разрядной ячейке памяти в формате со знаком.

Число 157 в 8-разрядной ячейке памяти в формате со знаком представить невозможно, так как максимальное положительное число, которое умещается в 8 разрядов — это 127. 7 разрядов занимает собственно число и 1 разряд — знак.

4. Получите внутреннее представление числа -157 в 8-разрядной ячейке памяти в формате со знаком.

Число -157 в 8-разрядной ячейке памяти в формате со знаком представить невозможно, так как максимальное отрицательное число, которое умещается в 8 разрядов — это -128.

5. Почему множество действительных (вещественных) чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?

6. На какие две части делится число в формате с плаваю щ ей запятой?

Внутреннее представление вещественных чисел в памяти компьютера

Представление чисел в формате с фиксированной запятой. Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «запятая» «находится» справа после младшего разряда, то есть вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А₂ = = 11110000₂ будет храниться в ячейке памяти следующим образом:

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно

А = 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 = 1 × 2 8 — 1 = 255₁₀.

Диапазон изменения целых неотрицательных чисел чисел: от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1).

Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа. Например, число 2002₁₀ = 11111010010₂ будет представлено в 16-разрядном представлении следующим образом:

Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно:

Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.

Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2 n — |A|.

Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, так как в n-разрядной компьютерной арифметике:

поскольку в компьютерной n-разрядной арифметике 2 n = 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, то есть n нулей.

Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:

1. Модуль числа записать в прямом коде в n двоичных разрядах.

2. Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).

3. К полученному обратному коду прибавить единицу.

Запишем дополнительный код отрицательного числа -2002 для 16-разрядного компьютерного представления:

При n-разрядном представлении отрицательного числа А в дополнительным коде старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число

Чтобы число было положительным, должно выполняться условие

Следовательно, максимальное значение модуля числа А в га-разрядном представлении равно:

Тогда минимальное отрицательное число равно:

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится четыре ячейки памяти — 32 бита).

Максимальное положительное целое число (с учетом выделения одного разряда на знак) равно:

А = 2 31 — 1 = 2 147 483 647₁₀.

Минимальное отрицательное целое число равно:

А = -2 31 = — 2 147 483 648₁₀.

Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций.

Недостатком представления чисел в формате с фиксированной запятой является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.

Представление чисел в формате с плавающей запятой. Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. В этом случае положение запятой в записи числа может изменяться.

Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так число А может быть представлено в виде:

A = m × q n

2.3

где m — мантисса числа;
q — основание системы счисления;
n — порядок числа.

Для единообразия представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:

Здесь нормализованная мантисса: m = 0,55555, порядок: n = 3.

Число в формате с плавающей запятой занимает в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности). При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы.

Определим максимальное число и его точность для формата чисел обычной точности, если для хранения порядка и его знака отводится 8 разрядов, а для хранения мантиссы и ее знака — 24 разряда:

0	1	1	1	1	1	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
знак и порядок								знак и мантисса

Максимальное значение порядка числа составит 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа составит:

2 127 = 1,7014118346046923173168730371588 × 10 38 .

Максимальное значение положительной мантиссы равно:

2 23 — 1 » 2 23 = 2 (10 × 2,3) » 1000 2,3 = 10 (3 × 2,3) » 10 7 .

Таким образом максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411 × 10 38 (количество значащих цифр десятичного числа в данном случае ограничено 7 разрядами).

1.26. Заполнить таблицу, записав отрицательные десятичные числа в прямом, обратном и дополнительном кодах в 16-разрядном представлении:

Десятичные числа	Прямой код	Обратный код	Дополнительный код
-50
-500

1.27. Определить диапазон представления целых чисел со знаком (отводится 2 байта памяти) в формате с фиксированной запятой.

1.28. Определить максимальное число и его точность для формата чисел двойной точности, если для хранения порядка и его знака отводится 11 разрядов, а для хранения мантиссы и ее знака — 53 разряда.

Объясните задачу про представление вещественных чисел в памяти компьютера

Собственно знать как и что представляется в компе — необходимо, а особенно как представляются вещественные числа.

Как я рассуждаю:
1). в задачи речь идёт о типе float(вещественный, да и с 4-мя байтами. Это однозначно он)
2). я понял как вычислили число 127, но я понять не могу, почему именно 2 127 (почему именно 2, а не 10?)
3). Вот тут у меня вообще тёмный лес: 2 23 – 1 ≈ 2 23 = 2 (102,3) ≈ 1000 2,3 = 10 (32,3) ≈ 107. (тут возможны ошибки, на скрине всё нормально написано).

Будьте добры объяснить новечку что и как/откуда тут берётся, буду крайне благодарен.

Скрин задачи прилагаю (там где не понятно выделил).

Представление вещественных чисел в памяти ЭВМ
Помогите разобраться как представляются вещественные числа в памяти ЭВМ написал прогу masm .

Записать представление вещественных чисел в памяти ЭВМ на основе стандарта IEEE 754
Здравствуйте! Помогите пожалуйста с лабораторной работой, очень срочно

Внутреннее представление чисел в памяти компьютера. Проверить правильность решения
Не понимаю формулировку задания:в формат числа со знаком и числа без знака (использовать формат.

Представление графа в памяти компьютера
Составьте программу, которая содержит функцию (или процедуру) создания заданного способа.

в памяти все хранится в двоичной системе, поэтому логично, что 2, а не 10
порядок — это степень, в которое возводится основание системы счисления. основание 2. поэтому 2^127
теперь по поводу мантиссы. там 24 бита. 1 бит это знак. остается 23 бита. сколько разных чисел можно получить с их помощью? 2^23. очевидно, одно из чисел будет нулем. следовательно, наибольшее число 2^23 — 1. минус единицей можно пренебречь для упрощения дальнейших расчетов.
далее 23=10*2.3
возведем 2 в степень 10. получим 1024. это примерно равно 1000. пишем 1000 для упрощения.
очевидно 1000=10^3
получаем 10^(3*2.3) = 10^(6.9)
округляем степень до 7

История науки и техники Com New

Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.

Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 – 1 = 255 = 11111111и минимальное 0 = 00000000. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255.

В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536 = 0000001000011000будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536 = 1000001000011000 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 – 1 = 2 – 1 = 2 – 1 = 32767 = 111111111111111 и диапазон чисел будет находиться в пределах от -32767 до 32767.

Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.

Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:

1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;

2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);

3) к полученному обратному коду прибавить единицу к младшему разряду.

Например, для числа -536 в таком формате модуль будет равен 0000001000011000, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536, т. е. число 536, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.

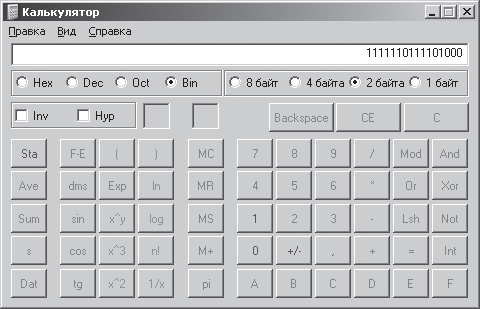
Рис. 2.6. Результат получения дополнительного кода

Необходимо помнить, что дополнительный код положительного числа – само число.

Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 – 1) … + 2 – 1 и -(2-1) … + 2 – 1.

Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).

Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.

Внутреннее представление вещественных чисел в памяти компьютера

©Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — авторский с подробными пояснениями профильными специалистами. Вы сможете скачать гдз, решебники, улучшить школьные оценки, повысить знания, получить намного больше свободного времени.

Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.

Внутреннее представление вещественных чисел в памяти компьютера

§ 17. Числа в памяти компьютера

Основные темы параграфа:

♦ представление целых чисел;
♦ размер ячейки и диапазон значений чисел;
♦ особенности работы компьютер с целыми числами;
♦ представление вещественных чисел;
♦ особенности работы компьютера с вещественными числами.

Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном счете сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1. Поэтому современные компьютерные технологииназывают цифровыми технологиями.

В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.

Представление целых чисел

Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальная ячейка, в которой может храниться целое число, имеет размер 8 битов — 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете. Результат перевода:

Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так:

Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.

Самый старший разряд — первый слева, хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:

Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 2 7 = 128. Значит:

01111111₂ = 128 — 1 = 127.

Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.

Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25? Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. К сожалению, в компьютере все несколько сложнее.

Для представления отрицательных целых чисел используется дополнительный код.

Получить дополнительный код можно по следующему алгоритму:

1) записать внутреннее представление положительного числа X;
2) записать обратный код этого числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.

Определим по этим правилам внутреннее представление числа -25₁₀ в 8-разрядной ячейке:

1) 00011001
2) 11100110
3) +1
11100111 — это и есть представление числа -25.

В результате выполнения такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.

Проверим полученный результат. Очевидно, что при сложении чисел +25 и -25 должен получиться ноль.

00011001
+11100111
1 00000000

Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается ноль!

Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.

Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 2 6 .

Размер ячейки к диапазон значений чисел

Наибольшее по модулю отрицательное значение в 8-разрядной ячейке равно -2 7 = -128. Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий:

-128 X 127, или -2 7 X 2 7 — 1.

Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим:

-2 15 X 2 15 — 1, или -32 768 X 32 767.

Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки:

-2 N-1 X 2 N-1 -1.

Диапазон для 32-разрядной ячейки получается достаточно большим:

-2 31 Х 2 31 — 1, или
-2 147 483 648 X 2 147 483 647.

Особенности работы компьютера с целыми числами

Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности диапазона допустимых значений. Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.

Представление вещественных чисел

Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с вещественными числами.

Всякое вещественное число (X) можно записать в виде произведения мантиссы m и основания системы счисления р в некоторой целой степени n, которую называют порядком:

Например, число 25,324 можно записать в таком виде: 0,25324 · 10 2 . Здесь m = 0,25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.

Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел. Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.

Особенности работы компьютера с вещественными числами

1. Диапазон вещественных чисел ограничен. Но он значительно шире, чем для рассмотренного ранее способа представления целых чисел. Например, при использовании 32-разрядной ячейки этот диапазон следующий:

-3,4 · 10 38 X 3,4 · 10 38 .

2. Выход за диапазон (переполнение) — аварийная ситуация для процессора, который прерывает свою работу.
3. Результаты машинных вычислений с вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшается.

Коротко о главном

В памяти компьютера целые числа представляются в двоичной системе счисления и могут занимать ячейку размером 8, 16, 32 и т. д. битов.

Диапазон значений целых чисел ограничен. Чем больше размер ячейки, тем шире диапазон.

При выходе результатов вычислений с целыми числами за допустимый диапазон работа процессора не прерывается. При этом результаты могут оказаться неверными.

Вещественные числа представляются в виде совокупности мантиссы и порядка в двоичной системе счисления. Обычный размер ячейки — 32 или 64 бита.

Результаты вычислений с вещественными числами приближенные. Переполнение приводит к прерыванию работы процессора.

Вопросы и задания

1. Как в памяти компьютера представляются целые положительные и отрицательные числа?
2. Укажите, каков был бы диапазон значений целых чисел, если бы для их хранения использовалась 4-разрядная ячейка.
3. Запишите внутреннее представление следующих десятичных чисел, используя 8-разрядную ячейку.
а) 32; б) -32; в) 102; г) -102; д) 126; е) -126.
4. Определите, каким десятичным числам соответствуют следующие двоичные коды 8-разрядного представления целых чисел.
а) 00010101; б) 11111110; в) 00111111; г) 10101010.

И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов

_{Планы уроков информатики, скачать тесты бесплатно, всё для учителя и школьника в подготовке к уроку по информатике 9 класс, домашние задания, вопросы и ответы}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.