Принципы организации ЭВМ
- 1. Название «электронная вычислительная машина» говорит о том, что эта машина предназначена, во-первых, для решения сложных вычислительных задач, и во-вторых, что она должна быть реализована на базе электронных элементов.
- 2. ЭВМ — это машина с хранимой (в памяти ЭВМ) программой, представленной в виде последовательности команд.
- 3. Составляющие выполняемую ЭВМ программу команды и данные, над которыми выполняются задаваемые командами операции, должны быть представлены в ЭВМ в виде двоичного кода.
- 4. Память ЭВМ должна быть организована в виде последовательности запоминающих ячеек, в каждой из которых может храниться (запоминаться) какой-либо двоичный код (код команды, числа, символа алфавита). При этом в конкретный момент времени можно обратиться для записи или чтения к любой одной из этих ячеек независимо от места ее расположения в памяти, указав адрес (порядковый номер) этой ячейки.
- 5. Для хранения кодов команд и кодов данных в ЭВМ используется одна общая память. При этом в двоичных кодах самих команд и данных отсутствуют какие-либо признаки, позволяющие явно отличать команды от данных.
- 6. Предназначение содержащихся в ячейках памяти данных, их тип и способ интерпретации и обработки также явно в их двоичном коде не указываются.
- 7. В классической фоннеймановской ЭВМ используется один центральный процессор.
Обращаясь к предыстории ЭВМ, можно отметить, что большинство из приведенных принципов сами по себе в отдель-
ности не являются оригинальным изобретением создателей первых ЭВМ, а в том или ином контексте уже ранее встречались в вычислительных устройствах. Заслугой первых разработчиков ЭВМ является то, что они отобрали из богатого предшествующего опыта наиболее эффективные решения, собрав их в единый комплекс, что и позволило наконец создать это одно из самых феноменальных изобретений человека.
Рассмотрим приведенные выше принципы более подробно, пытаясь определить мотивацию создателей ЭВМ при выборе этих решений.
ЭВМ — это машина с хранимой (в памяти ЭВМ) программой, представленной в виде последовательности команд.
В этом тезисе содержится два ключевых слова — «программой» и «хранимой».
Первое означает, что в основу способа, с помощью которого ЭВМ становится способной решать какую-либо сложную задачу — а создавалась она для решения сложных вычислительных задач, — должен быть положен принцип программирования. Это означает, что решение сложной задачи должно быть представлено в виде последовательности выполнения достаточно простых действий (другими словами, представлено в виде программы, состоящей из последовательности элементарных опе- раций/команд).
Для создателей ЭВМ тут являлось важным то, что составляющие такую программу операции могли быть настолько простыми, что их становилось возможным практически реализовать с помощью устройств, имевшихся в то время в распоряжении разработчиков ЭВМ. Заметим, что к тому времени стало очевидным, что элементной базой, наиболее подходящей для создания ЭВМ, могут быть не механические, а только электронные элементы, как наиболее быстродействующие физические устройства.
Второе ключевое слово — «хранимой» — означает, что в ЭВМ должно быть специальное устройство, способное запоминать, хранить и, самое главное, быстро выдавать в нужном порядке для исполнения команды, составляющие такую программу. Мы это устройство называем «память ЭВМ».
Следующий принцип посвящен тому, в каком виде должны быть представлены в ЭВМ команды и данные.
Выполняемые ЭВМ команды и данные, над которыми выполняется задаваемая командой операция, должны быть представлены в ней в виде двоичного кода.
Казалось бы, совершенно очевидно, что для представления чисел и произведения вычислений над ними наиболее естественным для человека является десятичное представление. Однако для реализации ЭВМ ее создателями было выбрано именно двоичное представление. И причина этого опять определяется соображениями простоты реализации носителей такого кода с помощью физических (а именно электронных) элементов. Реализовать электронный элемент, способный находиться всего в двух состояниях, принципиально проще, чем элемент с большим числом состояний.
Если выше декларировалось, что в ЭВМ обязательно должно быть запоминающее устройство для запоминания двоичных кодов команд и данных, то в следующем принципе определялась конструкция такого запоминающего устройства.
Память ЭВМ должна быть организована в виде последовательности одинаковых запоминающих ячеек, в каждой из которых может храниться (запоминаться) некоторый двоичный код — код команды ЭВМ, код числа или символа алфавита; при этом в конкретный момент времени можно обратиться для записи или чтения к любой одной из этих ячеек независимо от ее расположения в памяти (в начале, в середине, в конце), указав адрес (порядковый номер) этой ячейки.
Запоминающее устройство, организованное таким образом, называется памятью с произвольным доступом.
Хотя сама по себе способность к запоминанию чего-либо хорошо знакома человеку — у каждого из нас есть своя память, конструкция предложенной для ЭВМ памяти ничего общего с нашей собственной человеческой памятью не имеет. И опять создатели ЭВМ исходили из соображений реализуемости такого запоминающего устройства с помощью имевшихся в их распоряжении электронных элементов. Важным также является тот факт, что организация памяти в виде последовательности запоминающих ячеек хорошо согласуется с задачей хранения и быстрой выборки последовательности команд, составляющих выполняемую ЭВМ программу.
Отметим, однако, что память с произвольным доступом, даже применительно к ЭВМ, вообще говоря, является не единственно возможным и практически используемым способом реализации ее запоминающего устройства. В частности, чуть позже в рамках этого курса мы рассмотрим память, организованную в виде стека, в которой понятие адреса ячейки отсутствует; можно упомянуть также так называемую ассоциативную память, в которой обращение осуществляется не по адресу запоминающего элемента, а по его содержимому. Тем не менее в данный момент мы ведем речь именно о памяти с произвольным доступом.
Интересен следующий тезис.
В ЭВМ используется одна общая память как для хранения данных, так и для хранения команд. При этом в двоичных кодах самих данных и команд отсутствуют признаки, позволяющие явно отличать их друг от друга.
Казалось бы, коды команд и коды данных по сути являются совершенно разными сущностями с точки зрения их интерпретации и обработки в ЭВМ. Код команды определяет, какие действия должна выполнить ЭВМ, а данные — это объекты, над которыми эти действия выполняются. И тем не менее мы «складываем» эти объекты в одну общую память и отказываемся даже от того, чтобы как-то пометить их, чтобы различить. Дело в том, что, как будет видно дальше, сформулированные принципы реализации ЭВМ на самом деле позволяют реализовать корректную быструю выборку из памяти и последующую интерпретацию и использование двоичных кодов команд и данных при их размещении в одной общей памяти и отсутствии в их коде признаков, обозначающих тип этих кодов.
При этом существенным выигрышем является гораздо более эффективное использование всегда ограниченного количества ячеек запоминающего устройства (пространства памяти) в условиях, когда заранее не известно, сколько ячеек потребуется для размещения команд, а сколько — для данных.
Справедливости ради отметим, что в конце 1930-х гг. в Гарвардском университете Говардом Эйкеном была предложена иная архитектура запоминающего устройства вычислительной машины. Идея, реализованная Эйкеном, заключалась в физическом разделении устройств хранения и линий передачи команд и данных.
И тем не менее для ЭВМ фоннеймановской архитектуры (ее еще называют принстонской) было выбрано решение с общей памятью для команд и данных. То, что это было не самое плохое решение, подтверждается тем фактом, что и в настоящее время в большинстве компьютеров используется именно общая память для команд и для данных.
Однако не была забыта и гарвардская архитектура с раздельной памятью для команд и данных. В 90-е гг. XX в. она возродилась при создании так называемых процессоров сигналов, то есть процессоров, предназначенных для обработки сигналов в реальном масштабе времени, для которых фактор скорости выполнения операций оказался гораздо более приоритетным, чем оптимизация использования имеющегося объема памяти ЭВМ.
Следующий тезис обсуждаемого перечня фоннеймановских принципов реализации ЭВМ перекликается с предыдущим и гласит, что в двоичном коде данных также не содержится признаков, обозначающих предназначение данных, их тип и способ использования.
То есть даже зная, что данный двоичный код представляет какие-то данные, мы не можем сказать, что это: целое число без знака, число со знаком, число с плавающей точкой, код символа какого-то алфавита. Эти характеристики определяются и различаются в контексте выполняемой ЭВМ программы.
Наконец, последний тезис фоннеймановских принципов говорит о том, что в классической фоннеймановской ЭВМ используется один центральный процессор. Вполне понятно, что при создании первых ЭВМ их разработчики в сторону многопроцессорных вычислительных систем еще не глядели.
Данные
Данные (англ. data) – это информация собранная и трансформированная для некоторых целей, обычно анализа. Это может быть любой символ, текст, цифры, картинки, звук или видео. Данные вне контекста обычно не понятны человеку или компьютеру.

Внутри хранилища компьютера, данные представляют собой набор чисел, представленных в виде байтов, которые в свою очередь состоят из битов, имеющих значение один или ноль. Данные обрабатываются процессором, использующим логические операции для получения новых данных из исходных.
В какой системе исчисления хранит данные компьютер
Дорогие читатели! Редакция сайта iXBT.com обращается к вам с просьбой отключить блокировку рекламы на нашем сайте.
Редакция сайта iXBT.com обращается к вам с просьбой отключить блокировку рекламы на нашем сайте.
Дело в том, что деньги, которые мы получаем от показа рекламных баннеров, позволяют нам писать статьи и новости, проводить тестирования, разрабатывать методики, закупать специализированное оборудование и поддерживать в рабочем состоянии серверы, чтобы форум и другие проекты работали быстро и без сбоев.
Мы никогда не размещали навязчивую рекламу и не просили вас кликать по баннерам. Вашей посильной помощью сайту может быть отсутствие блокировки рекламы.
Преобразование десятичных чисел в 16- систему
И того получим 1B.
Рассмотрим несколько простых примеров шестнадцатеричной арифметики. Следует помнить, что после шестнадцатеричного числа F следует шестнадцатеричное 10, что равно десятичному числу 16:
Системы счисления
Жизнь человека невозможно представить без счета. Мы считаем постоянно – время до начала любимой передачи, сдачу в магазине, решая математические задачи. При этом для счета мы используем 10 цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Именно поэтому эту систему счисления называют десятичной – в ней 10 цифр. Комбинируя эти цифры можно получать бесконечное множество чисел. А можно ли использовать большее или меньшее количество цифр?
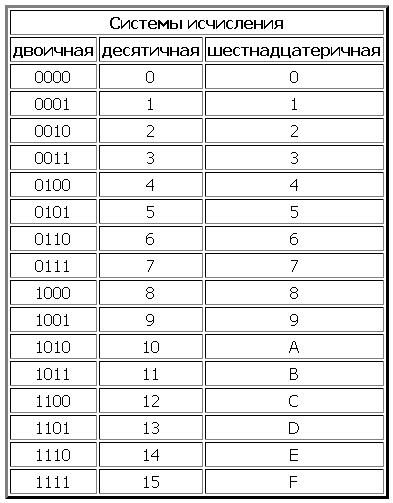
Конечно! Мы используем 10 цифр по простой причине – для счета удобно пользоваться пальцами рук, а у нас их 10. А вот, например, в памяти компьютера вся информация записана с помощью только двух цифр – 0 и 1. Соответственно, такая система счисления называется двоичная. Число, записанное в двоичной системе счисления можно представить в десятичной системе и наоборот. Система счисления определяет способ записи чисел и правила выполнения действий над ними. Помимо двоичной и десятичной систем счисления наиболее популярными являются восьмеричная и шестнадцатеричная. По аналогии можно предположить, что в восьмеричной системе счисления для записи чисел используют 8 цифр – 0, 1, 2, 3, 4, 5, 6, 7. А что же с шестнадцатеричной системой счисления? Ведь мы знаем только 10 цифр – от 0 до 9. А в шестнадцатеричной системе используется 16 цифр. Где взять недостающие 6 цифр? Очень просто – для записи цифр от 10 до 15 использовать… буквы A, B, C, D, E, F. И тогда число в шестнадцатеричной системе счисления можно записать используя цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Количество цифр, которые используются для записи чисел называется основанием системы счисления. Например, у двоичной системы счисления основание равно двум, а у восьмеричной – восьми. А совокупность всех чисел, которые используются для записи чисел называют алфавит. Эту информацию нагляднее представить в виде таблицы:
| Название системы счисления | Основание системы счисления | Алфавит системы счисления |
| двоичная | 2 | 0, 1 |
| восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
А как определить в какой системе счисления записано число? Для этого после числа в нижнем индексе указывается основание системы счисления, в которой записано число. Например,
101102 – число в двоичной системе счисления,
52316 – число в шестнадцатеричной системе счисления,
538 – число в восьмеричной системе счисления,
72310 – число в десятичной системе счисления.
Все системы счисления описанные выше называются позиционными. Это значит что значение цифры зависит от позиции, на которой оно находится. К примеру, возьмем два числа в десятичной системе счисления – 237 и 723. Хотя эти числа и состоят из одних цифр, но эти числа разные, так как в первом числе цифра 2 означает сотни, а во втором – десятки и т. д.
Системы счисления, в которых значение цифры не зависит от ее положения в числе называют непозиционными. Ярчайший пример такой системы – римская запись числа. Если мы рассмотрим римское число III, то увидим, что на какой бы позиции не стояла цифра I она везде означает единицу.
Для перевода чисел из десятичной системы счисления в любую другую рекомендую использовать этот скрипт
Вариант 1
1. Если число отрицательное, то в знаковый разряд помещается
2. Числом в нормальной форме с нормализованной мантиссой (правильной дробью, имеющей после запятой цифру, отличную от нуля) является
1) 7815
2) 2783,00029
3) 0,03428
4) 0,401 x 10 7
3. Беззнаковым 8-разрядным представлением числа 4510 является
1) 00101101
2) 101101
3) 10110100
4) 00000101
4. Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?
5. При записи числа в форме A = ± m x q p , где q — это
1) мантисса
2) само вещественное число
3) порядок числа
4) основание системы счисления
6. Укажите десятичный эквивалент числа, прямой код которого 00010101 записан в 8-разрядном формате со знаком
1) 21
2) 34
3) -21
4) верного ответа в предложенных вариантах нет
7. Укажите число, записанное в естественной форме
1) 2010,0102
2) 1,784824E+5
3) 95400611 x 10 2
4) среди предложенных вариантов нет числа в естественной форме
Ответы на тест по информатике Представление чисел в компьютере для 8 класса
Вариант 1
1-4
2-1
3-4
4-14
5-3
6-2
7-3
Вариант 2
1-2
2-4
3-1
4-23
5-4
6-1
7-1