Уроки 6 — 7§ 1.2. Представление чисел в компьютере

Презентация Представление чисел в памяти ПК
презентация к уроку по информатике и икт (10 класс)

31.08.20 Цель урока: Знакомство с представлением чисел в памяти компьютера.

Главные правила представления данных в компьютере Данные и программы в памяти компьютера хранятся в двоичном виде. Представление данных в компьютере дискретно. Множество представимых в памяти величин ограничено и конечно. В памяти компьютера числа хранятся в двоичной системе счисления.

Любая информация в памяти компьютера представляется с помощью нулей и единиц, то есть с помощью двоичной системы счисления. Первоначально компьютеры могли работать только с числами. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа сводится к обработке двоичных чисел – чисел, записываемых с помощью двух цифр – 0 и 1. В компьютере различаются два типа числовых величин: целые числа и вещественные (действительные) числа. Различаются способы представления их в памяти компьютера.

Часть памяти, в которой хранится одно число, называется ячейка . Минимальный размер ячейки, в которой может храниться целое число, — 8 битов, или 1 байт.

31.08.20 Представим число 15 в памяти компьютера . Для этого мы должны перевести его в двоичную систему счисления. 1 1 1 1 0 0 0 0 Мы получили внутреннее представление числа.

Вспомним из 9 класса Алгоритм перевода десятичного числа в двоичное число Последовательно делить «в столбик» исходное десятичное число и получаемые частные на 2 до тех пор, пока частное не станет равным 1. 2. Полученные остатки от деления (это будут 0 или 1) записать справа налево, начиная с последнего частного. Это и будет значение числа в двоичной системе.

Пример перевода десятичного числа в двоичное число 23 10 =10111 2

Сложение двоичных чисел 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 1 0 1 + 1 1 1 1 + 1 1 0 0 Таблица сложения: 1

31.08.20 Алгоритм представления отрицательных целых чисел в компьютере Перевести модуль данного отрицательного числа в двоичную систему счисления. Дописать впереди нули, заполнив всю разрядную сетку (прямой код). Заменить нули на единицы, а единицы на нули (инвертировать) (обратный код). К полученному числу в столбик прибавить 1 (дополнительный код).

31.08.20 Определим внутреннее представление числа -15 10 в восьмиразрядной сетке. Запишем внутреннее представление числа 15 10 – 00001111 (переведем в двоичную систему и добавим впереди нули до 8 разрядов) Запишем обратный код – 11110000 К полученному числу прибавим 1 – 11110001 Первый бит указывает на знак числа. Если он = 0, то число положительное, если = 1, то число отрицательное. 1 0 0 0 1 1 1 1

31.08.20 Разряд и диапазон ячеек В восьмиразрядной ячейке можно получить числа диапазоном -128 Пример 1. Определить прямой, обратный и дополнительный коды следующих двоичных чисел: а)100100; б) -100011; в) -100100. Решение Будем считать, что число размещается в двух байтах. Старший бит – знак разряда. Незначащие нули добавляются слева от числа. Результат представим в виде таблицы: Число Прямой код Обратный код Дополнительный код 100100 0000000000100100 0000000000100100 0000000000100100 -100011 1000000000100011 1111111111011100 1111111111011101 -100100 1000000000100100 1111111111011011 1111111111011100 Пример 2. Как будет представлено в памяти компьютера целое число 12345 10 ? Решение Для размещения числа возьмем два байта. Поскольку число положительное, то в старшем (15-м) бите будет 0. Переведем число в двоичную систему счисления: 12345 10 = 11000000111001 2 . Результат: 0 0110000 00111001 Знак числа число

Домашнее задание Прочитать параграф 19 и письменно выполнить задания: Запишите внутреннее представление десятичных чисел, используя 8-разрядную ячейку: а) 64 б) -58 в) 37 г) -96 2. Запишите внутреннее представление десятичных чисел, используя 16-разрядную ячейку: а) 25 б) -25 в) 84 г) -62 Примечание : Положительные числа достаточно перевести в двоичную систему счисления и дописать впереди нули до 8 или до 16 разрядов. Для отрицательных чисел нужно выполнить все 4 пункта алгоритма (он представлен выше в презентации).

2.2. Представление вещественных чисел

Любое вещественное число А может быть записано в экспоненциальной форме:

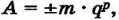
где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Например, число 472 000 000 может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.

Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».

Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 10 9 .

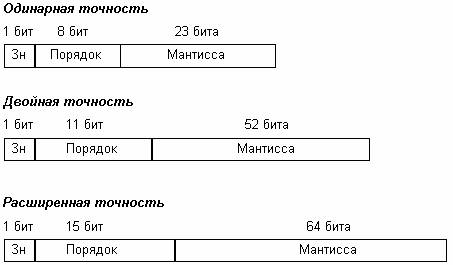
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа:

0,11111111111111111111111 • 10 1111111

Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

Вещественные числа (числа с плавающей точкой)

Все равные по абсолютному значению положительные и отрицательные числа отличаются только этим битом. В остальном числа с разным знаком полностью одинаковы. Для представления отрицательных чисел здесь не используется дополнительный код.
Поле мантиссы содержит мантиссу нормализованного числа.
Одинарная точность:
1.(цифры мантиссы)*2 (P-127)
Двойная точность:
1.(цифры мантиссы)*2 (P-1023)
Расширенная точность:
1.(цифры мантиссы)*2 (P-16383)

Пример .
Запишите код действительного числа, интерпретируя его как величину типа Double.
а) 446,15625;
Переводим десятичное число в двоичное представление.

Целая часть от деления	Остаток от деления
446 div 2 = 223	446 mod 2 = 0
223 div 2 = 111	223 mod 2 = 1
111 div 2 = 55	111 mod 2 = 1
55 div 2 = 27	55 mod 2 = 1
27 div 2 = 13	27 mod 2 = 1
13 div 2 = 6	13 mod 2 = 1
6 div 2 = 3	6 mod 2 = 0
3 div 2 = 1	3 mod 2 = 1
1 div 2 = 0	1 mod 2 = 1

Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 110111110
446 = 110111110₂
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.15625*2 = 0.313 (целая часть 0)
0.313*2 = 0.626 (целая часть 0)
0.626*2 = 1.252 (целая часть 1)
0.252*2 = 0.504 (целая часть 0)
0.504*2 = 1.008 (целая часть 1)
Получаем число в 2-ой системе счисления: 00101

0.15625 = 00101₂
446.15625 = 110111110,00101₂ = 1,1011111000101*2 8

Знак S = 0
Порядок P = 8 + 1023 = 1031₁₀ = 10000000111₂
Мантисса: 1011111000101
Для числа с двойной точностью мантисса занимает 52 разряда. Добавляем нули.
Мантисса: 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
0 10000000111 1011 1110 0010 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: 407BE28000000000₁₆

б) -455,375.
Переводим десятичное число в двоичное представление.

Целая часть от деления	Остаток от деления
455 div 2 = 227	455 mod 2 = 1
227 div 2 = 113	227 mod 2 = 1
113 div 2 = 56	113 mod 2 = 1
56 div 2 = 28	56 mod 2 = 0
28 div 2 = 14	28 mod 2 = 0
14 div 2 = 7	14 mod 2 = 0
7 div 2 = 3	7 mod 2 = 1
3 div 2 = 1	3 mod 2 = 1
1 div 2 = 0	1 mod 2 = 1

Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 111000111
455 = 111000111₂
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.375*2 = 0.75 (целая часть 0)
0.75*2 = 1.5 (целая часть 1)
0.5*2 = 1 (целая часть 1)
0*2 = 0 (целая часть 0)
Получаем число в 2-ой системе счисления: 0110
0.375 = 0110₂

455,375 = 111000111,0110₂ = 1,110001110110*2 8 ₂

Знак S = 1
Порядок P = 8 + 1023 = 1031₁₀ = 10000000111₂
Мантисса: 1100 0111 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
Запишем число:
1 10000000111 1100 0111 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
В шестнадцатеричной системе счисления: -455,375 = C07C760000000000₁₆

Дан код величины типа Double. Преобразуйте его число.
а) 408B894000000000;
Представим в двоичном коде:
010000001000 1011 1000 1001 0100 0000 0000 0000 0000 0000 0000 0000 0000 0000
где
S = 0 (положительное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 10111000100101
N = 1,10111000100101
С учетом P = 9, N = 1101110001,00101

1101110001 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *1 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0+ 2 1 *0 + 2 0 *1 = 512 + 256 + 0 + 64 + 32 + 16 + 0 + 0 + 0 + 1 = 881

Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
00101 = 2 -1 *0 + 2 -2 *0 + 2 -3 *1 + 2 -4 *0 + 2 -5 *1 = 0.15625

б) C089930000000000.
Представим в двоичном коде:
1 10000001000 100110010011000000000000000000000000 0000 0000 0000 0000
где
S = 1 (отрицательное число)
P = 10000001000₂ = 1032 – 1023 = 9
M = 100110010011
N =1,100110010011
С учетом P = 9, N = 1100110010,011

1100110010 = 2 9 *1 + 2 8 *1 + 2 7 *0 + 2 6 *0 + 2 5 *1 + 2 4 *1 + 2 3 *0 + 2 2 *0 + 2 1 *1 + 2 0 *0 = 512 + 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0 = 818

Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
011 = 2 -1 *0 + 2 -2 *1 + 2 -3 *1 = 0.375

Выход РФ из ВОЗ. Прямая трансляция

Алгоритм получения дополнительного кода отрицательного числа.

1. модуль отрицательного числа представить прямым кодом в k двоичных разрядах;
2. значение всех бит инвертировать:все нули заменить на единицы, а единицы на нули(таким образом, получается k-разрядный обратный код исходного числа);
3. к полученному обратному коду прибавить единицу.

Пример:
Получим 8-разрядный дополнительный код числа -52:

Можно заметить, что представление целого числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:

Представление целых чисел

Тебе известно, что компьютер работает только с двоичным кодом. (0) и (1) обозначают два устойчивых состояния: вкл/выкл, есть ток/нет тока и т. д. Оперативная память представляет собой контейнер, который состоит из ячеек. В каждой ячейке хранится одно из возможных состояний: (0) или (1). Одна ячейка — (1) бит информации или представляет собой разряд некоторого числа.

Целые числа в памяти компьютера хранятся в формате с фиксированной запятой . Такие числа могут храниться в (8), (16), (32), (64)-разрядном формате.

Переведём двоичный код в десятичную систему счисления и узнаем самое большое число, которое можно сохранить в восьмибитном формате.

Если целое неотрицательное число больше (255), то оно будет храниться в (16)-разрядном формате и занимать (2) байта памяти, то есть (16) бит.

Для (n)-разрядного представления диапазон чисел можно вычислить следующим образом: от (0) до 2 n − 1 .

Запишем целое беззнаковое число (65) в восьмиразрядном представлении. Достаточно перевести это число в двоичный код.

Для целых чисел со знаком в памяти отводится (2) байта информации ((16) бит). Старший разряд отводится под знак: (0) — положительное число; (1) — отрицательное число. Такое представление числа называется прямым кодом.

Для хранения отрицательных чисел используют дополнительный и обратный коды, которые упрощают работу процессора. Но об этом ты узнаешь в старших классах.

История науки и техники Com New

Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.

Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 – 1 = 255 = 11111111и минимальное 0 = 00000000. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255.

В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536 = 0000001000011000будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536 = 1000001000011000 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 – 1 = 2 – 1 = 2 – 1 = 32767 = 111111111111111 и диапазон чисел будет находиться в пределах от -32767 до 32767.

Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.

Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:

1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;

2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);

3) к полученному обратному коду прибавить единицу к младшему разряду.

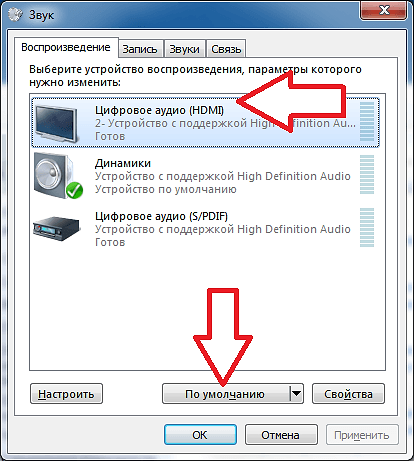
Например, для числа -536 в таком формате модуль будет равен 0000001000011000, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536, т. е. число 536, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.

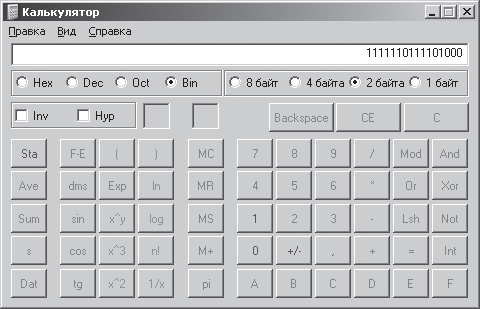
Рис. 2.6. Результат получения дополнительного кода

Необходимо помнить, что дополнительный код положительного числа – само число.

Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 – 1) … + 2 – 1 и -(2-1) … + 2 – 1.

Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).

Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.