Конспект урока Логические элементы 9 класс
Конспект урока Логические элементы (9 класс 1 часть, урок 12, учебник Босова Л.Л.). На данном уроке ученики знакомятся с понятиями: логический элемент, конъюнктор, дизъюнктор, инвертор и электронная схема.
Планируемые образовательные результаты:
— предметные – представление о логических элементах (конъюнкторе, дизъюнкторе, инверторе) и электронных схемах; умения анализа электронных схем;
— метапредметные – умения представления одной и той же информации в разных формах (таблица истинности, логическое выражение, электронная схема);
— личностные – понимание роли фундаментальных знаний как основы современных информационных технологий.
Решаемые учебные задачи:
1) знакомство с дискретными преобразователями информации и простейшими электронными схемами;
2) рассмотрение примеров анализа логических схем;
3) обобщение вопросов, связанных с теоретическими основами средств информационных технологий.
Основные понятия, изучаемые на уроке:
— логический элемент;
— конъюнктор;
— дизъюнктор;
— инвертор;
— электронная схема.
Используемые на уроке средства ИКТ:
— персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
— ПК учащихся.
Электронные образовательные ресурсы
— презентация «Логические элементы»;
— ресурсы федеральных образовательных порталов:
1) тренажер «Логика» (https://kpolyakov.spb.ru/prog/logic.htm);
2) информационный модуль «Достоинcтва и недостатки двоичной системы счисления при использовании ее в компьютере» (fcior.edu.ru).
Особенности изложения содержания темы урока
1. Организационный момент (1 минута)
Приветствие учащихся, сообщение темы и целей урока.
2. Повторение (14 минут)
1) визуальная проверка выполнения заданий в РТ;
2) рассмотрение заданий, вызвавших затруднения при выполнении
домашнего задания;
3) для закрепления навыка решения логических задач разбиваем класс на две группы и предлагаем каждой группе решить одну из задач №14, 15 к параграфу; способ решения задачи ученики выбирают самостоятельно.
3. Изучение нового материала (15 минут)
Новый материал излагается в сопровождении презентации «Логические элементы».
1 слайд — название презентации;
2 слайд — ключевые слова;
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
3 слайд — логический элемент;
4 слайд — конъюнктор;
5 слайд — дизъюнктор;
6 слайд — инвертор;
7 слайд — анализ электронной схемы 1; (задача №16 к параграфу)
8 слайд — анализ электронной схемы 2;
9 слайд — анализ электронной схемы 3;
Если позволяет время, то в процессе изложения нового материала используем тренажер «Логика».
4. Рефлексия. Обобщение всей темы (10 минут)
После рассмотрения нового материала рекомендуется на основе информационного модуля «Достоинства и недостатки двоичной системы счисления при использовании ее в компьютере» обобщить весь рассмотренный на уроках теоретический материал, связав его непосредственно с компьютерной техникой».
5. Подведение итогов урока. Сообщение домашнего задания. Выставление оценок (5 минут)
10 слайд — Домашнее задание.
§1.3 (п. 6); задание № 13 к параграфу;
№ 66, 67 в РТ.
Дополнительное задание: работа с тренажером «Логика».
Весь материал к уроку находится в архиве.
Скачать (91 КБ, rar): Конспект урока Логические элементы
Архив включает в себя:
— конспект,
— презентация.
Контрольные вопросы
1. Объясните действие электрических схем, реализующих модели логических элементов, с точки зрения законов постоянного тока.

Cкачать материалы урока
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
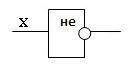
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
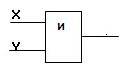
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
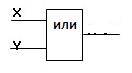
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.
Составьте логическую схему для логического выражения: F=A / B / A.
1. Две переменные – А и В.
2. Две логические операции: 1-/, 2-/.
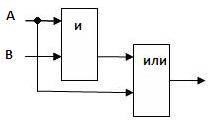
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: / и две /; А/В/ ¬ (В/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
Логические основы устройства компьютера
Компьютер работает на электричестве, т.е. логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают
сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом является таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
Базовые логические элементы реализуют рассмотренные выше три основные логические операции:
• логический элемент «И» — логическое умножение;
• логический элемент «ИЛИ» — логическое сложение;
• логический элемент «НЕ» — инверсию.
Т.к. любая логическая операция может быть представлена в виде комбинаций трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логический элемент «И».
На выходы А и В логического элемента (рис1) подаются два сигнала (00,01,10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.

Логический элемент «ИЛИ».

На входы А и В логического элемента (рис2) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
Логический элемент «НЕ».
На вход А логического элемента (рис3) подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.

Триггер-Это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю.
Термин «триггер» происходит от английского слова ТРИГГЕР-защелка, спусковой крючок. Самый распространенный тип триггера — так называемый РС — триггер. Он имеет 2 симметричных входа С и Р.
Что такое сумматор.
Сумматор-это электронная логическая схема, выполняющая суммирование двоичных чисел.
Сумматор служит прежде всего центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и других устройствах машины. Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров
Алгебра логики— это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности ) и логических операций над ними.
Таблица истинности — это таблица, в которой отражены все значения логической функции при всех возможных значениях, входящих в неё логически.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true либоfalse, 1 либо 0).

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
© cyberpedia.su 2017-2020 — Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
Логические основы работы компьютера
Процессор выполняет арифметические и логические операции над двоичными кодами. Поэтому необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Начнем с алгебры логики. Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями. Высказывание – это предложение, относительно которого имеет смысл говорить истинно оно или ложно. Высказывания могут быть представлены с помощью математических, химических и прочих знаков.
Алгебру логики называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: А, В, X, Y. В алгебре Буля введены три основные логические операции с высказываниями: сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.
Алгебра логики рассматривает высказывания не с точки зрения их содержания, а с точки зрения их истинности или ложности. И в этом смысле можно сказать, что высказывание может принимать только два значения: ИСТИНА (обозначим 1) или ЛОЖЬ (обозначим 0).
Логические выражения могут быть простыми и сложными. Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь». Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания. В качестве основных логических операций в сложных логических выражениях используются следующие: НЕ (логическое отрицание, инверсия); ИЛИ (логическое сложение, дизъюнкция); И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение — двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции, в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции.
Операция «НЕ» — логическое отрицание (инверсия) применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:
· если исходное выражение истинно, то результат его отрицания будет ложным;
· если исходное выражение ложно, то результат его отрицания будет истинным.
Для операции отрицания «НЕ» приняты следующие условные обозначения: ┐A; not А.
Результат операции отрицания «НЕ» определяется следующей таблицей истинности:
| A | ┐A |
| ложь | истина |
| истина | ложь |
| A | ┐A |
| 0 | 1 |
| 1 | 0 |
1. Высказывание «Земля вращается вокруг Солнца» истинно. Высказывание «Земля не вращается вокруг Солнца» ложно.
3. «4 — не простое число» истинно.
Принцип работы переключателя настольной лампы таков: если лампа горела, переключатель выключает ее, если лампа не горела — включает ее. Такой переключатель можно считать электрическим аналогом операции отрицания.

Операция «ИЛИ» –логическое сложение (дизъюнкция, объединение) выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции «ИЛИ» является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Результат операции «ИЛИ» определяется следующей таблицей истинности:
| A | B | A / B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Применяемые обозначения: А или В; A / В; A or В.
Результат операции «ИЛИ» истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
Примеры логического сложения.
1. Рассмотрим высказывание «В библиотеке можно взять книгу или встретить знакомого». Это высказывание формально можно представить так: С = A / В, где высказывание А — «В библиотеке можно взять книгу», а В — «В библиотеке можно встретить знакомого». Объединение этих высказываний при помощи операции логического сложения означает, что события могут произойти как отдельно, так и одновременно.
2. Рассмотрим высказывание «Знания или везение — залог сдачи экзаменов». Успешно сдать экзамен может тот, кто все знает, или тот, кому повезло (например, вытянут единственный выученный билет), или тот, кто все знает и при этом выбрал «хороший» билет.
3. Кто хоть однажды использовал елочную гирлянду с параллельным соединением лампочек, знает, что гирлянда будет светить до тех пор, пока цела хотя бы одна лампочка.
Логическая операция «ИЛИ» чрезвычайно схожа с работой подобной гирлянды, ведь результат операции ложь только в одном случае — когда все аргументы ложны.
Операция «И» –логическое умножение (конъюнкция) выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции «И» является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Результат операции «И» определяется следующей таблицей истинности:
| A | B | A / B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции «И» истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Примеры логического умножения.
1. Рассмотрим высказывание «Учитель должен быть умным и справедливым». Это высказывание формально можно представить так: С — А / В, где высказывание А — «Учитель должен быть умным», а В — «Учитель должен быть справедливым». Объединение этих высказываний при помощи операции логического умножения означает, что учитель должен быть одновременно и умным, и справедливым.
2. Рассмотрим высказывание «Умение и настойчивость приводят к достижению цели».
Достижение цели возможно только при одновременной истинности двух предпосылок — умения и настойчивости.
3. Логическую операцию «И» можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.
Операция «ЕСЛИ-ТО» – логическое следование (импликация) связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения: если А, то В; А влечет В; if A then В; А –> В.
| A | B | Если A, то B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
Примеры операции следования.
1. Рассмотрим высказывание «Если идет дождь, то на улице сыро». Здесь исходные высказывания «Идет дождь» и «На улице сыро». Если не идет дождь и не сыро на улице, результат операции следования — истина. На улице может быть сыро и без дождя, например, когда прошла поливочная машина или дождь прошел накануне. Результат операции ложен только тогда, когда дождь идет, а на улице не сыро.
2. Рассмотрим два высказывания: А делится на 9>, В х делится на 3>. Операция А –> В означает следующее: «Если число делится на 9, то оно делится и на 3». Рассмотрим возможные варианты:
· А — ложно, В — ложно (1-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то и В — ложно». Например, х = 4, 17, 22.
· А — ложно, В — истинно (2-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — ложно, то В — истинно». Например, х = 6, 12, 21.
· А — истинно, В — ложно (3-я строка таблицы истинности). Невозможно найти такие числа, которые делились бы на 9, но не делились на 3. Истинная предпосылка не может приводить к ложному результату импликации.
· А — истинно, В — истинно (4-я строка таблицы истинности). Можно найти такие числа, для которых истиной является высказывание «если А — истинно, то и В — истинно». Например, х = 9, 18, 27.
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность).
Применяемое обозначение: А ~ В.
| A | B | А ~ В |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
Примеры операции эквивалентности.
1. «День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом»;
2. «Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий».












