Уроки 2 — 5Системный анализ (§§ 1 — 4)Практическая работа № 1.1 Модели систем

Тест по дисциплине «Информационные технологии в профессиональной деятельности» для АНО ПО ОСЭК

Области, расположенные в верхнем и нижнем поле каждой страницы документа, которые обычно содержат повторяющуюся информацию:

b. совокупность методов, производственных процессов и программно-технических средств для обработки данных

Модель «черного ящика»

В простейшем случае бывает достаточно иметь представление о взаимодействии системы с внешней средой, не вдаваясь в подробности ее внутреннего устройства. Например, при использовании сложной бытовой техники вам совсем не обязательно знать ее устройство. Достаточно знать, как ею пользоваться, т. е. какие управляющие действия можно с ней производить (что на входе) и какие результаты вы будете при этом получать (что на выходе). Все эти сведения содержатся в инструкции для пользователя. Такое описание системы называется моделью «черного ящика» (рис. 1.2).

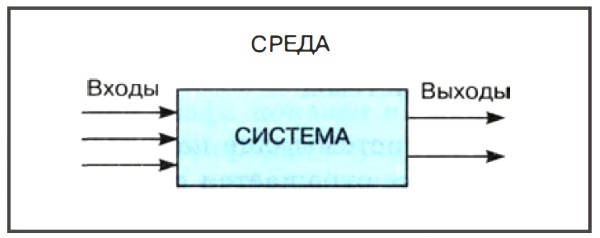
Вход системы — это воздействие на систему со стороны внешней среды, а выход — это воздействие, оказываемое системой на окружающую среду. В такой модели внутреннее устройство системы скрыто. Поэтому ее и называют «черным ящиком».

С точки зрения человека, не связанного с системой высшего образования, университет есть «черный ящик», на входе которого — выпускники школ, а на выходе — дипломированные специалисты.

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Информатика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.

Модель состава

Как отмечалось выше, результатом анализа системы является определение ее состава. Если описание системы ограничить перечислением ее частей, то мы получим модель состава. Например, модель состава системы «Университет» представлена на рис. 1.3.

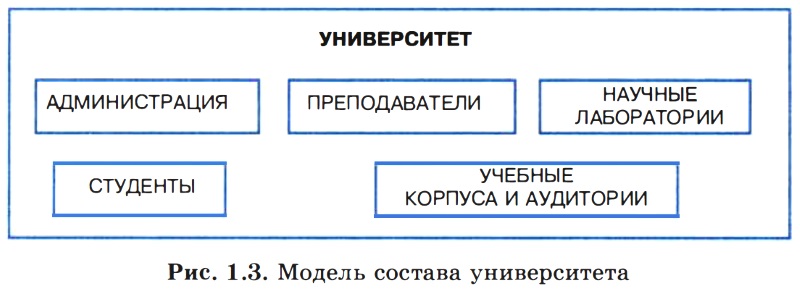
Каждая из отмеченных на рис. 1.3 составляющих системы «Университет» является подсистемой со своим составом. Поэтому для этих подсистем также можно построить свои модели состава. Разумеется, такой модели недостаточно для того, чтобы понять, как функционирует университет. И все-таки она дает более подробное представление об университете, чем модель «черного ящика».

Постройте ориентированный граф системы «Автомобиль», содержащий следующие вершины : руль, колеса, двигатель, педаль тормоза, педаль газа?

Постройте ориентированный граф системы «Автомобиль», содержащий следующие вершины : руль, колеса, двигатель, педаль тормоза, педаль газа.

Линия связи означает отношение «управление».

Является ли построенный граф деревом?

Модель «черного ящика»

В простейшем случае бывает достаточно иметь представление о взаимодействии системы с внешней средой, не вдаваясь в подробности ее внутреннего устройства. Например, при использовании сложной бытовой техники вам совсем не обязательно знать ее устройство. Достаточно знать, как ею пользоваться, т. е. какие управляющие действия можно с ней производить (что на входе) и какие результаты вы будете при этом получать (что на выходе). Все эти сведения содержатся в инструкции для пользователя. Такое описание системы называется моделью «черного ящика» (рис. 1.2).

Рис. 1.2. Модель «черного ящика»

Вход системы — это воздействие на систему со стороны внешней среды, а выход — это воздействие, оказываемое системой на окружающую среду. В такой модели внутреннее устройство системы скрыто. Поэтому ее и называют «черным ящиком».

С точки зрения человека, не связанного с системой высшего образования, университет есть «черный ящик», на входе которого — выпускники школ, а на выходе — дипломированные специалисты.

§ 2. Модели систем

Системный анализ

Исследование некоторой реальной системы состоит из двух этапов: этапа анализа и этапа синтеза.

Анализ системы — это выделение ее частей с целью прояснения состава системы. В предыдущем параграфе мы говорили, что каждая часть системы — это подсистема, и у этой подсистемы есть свои части. Однако невозможно раскладывать систему бесконечно. На чем-то придется остановиться, какие-то части принять за простые, далее неделимые элементы. Вопрос о том, на чем следует остановить «дробление» системы, зависит от цели исследования. Целью исследования системы является получение ее модели — приближенного представления об устройстве и функционировании системы. Полученная модель будет использоваться для прогнозирования поведения системы в некоторых условиях, для управления системой, для диагностики сбоев в функционировании системы и пр.

Однако невозможно понять механизм функционирования системы, выяснив только ее состав. Необходимо знать структуру связей между частями системы. Только в совокупности состава и структуры можно понять состояние и поведение системы. Поэто-му анализ системы — это первый этап ее исследования. Второй этап называется синтезом. Слово «синтез» означает соединение.

Синтез — это мысленное или реальное соединение частей в единое целое. В результате синтеза создается целостное представление о системе, объясняется механизм системного эффекта.

Системным анализом называется исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза.

Всякое описание системы носит модельный характер, т. е. отражает ограниченное число ее свойств. Главный вопрос при построении модели системы — какие ее характеристики являются существенными с точки зрения целей использования будущей модели?

Модель «черного ящика»

В простейшем случае бывает достаточно иметь представление о взаимодействии системы с внешней средой, не вдаваясь в подробности ее внутреннего устройства. Например, при использовании сложной бытовой техники вам совсем не обязательно знать ее устройство. Достаточно знать, как ею пользоваться, т. е. какие управляющие действия можно с ней производить (что на входе) и какие результаты вы будете при этом получать (что на выходе). Все эти сведения содержатся в инструкции для пользователя. Такое описание системы называется моделью «черного ящика» (рис. 1.2).

Вход системы — это воздействие на систему со стороны внешней среды, а выход — это воздействие, оказываемое системой на окружающую среду. В такой модели внутреннее устройство системы скрыто. Поэтому ее и называют «черным ящиком».

С точки зрения человека, не связанного с системой высшего образования, университет есть «черный ящик», на входе которого — выпускники школ, а на выходе — дипломированные специалисты.

Модель состава

Как отмечалось выше, результатом анализа системы является определение ее состава. Если описание системы ограничить перечислением ее частей, то мы получим модель состава. Например, модель состава системы «Университет» представлена на рис. 1.3.

Каждая из отмеченных на рис. 1.3 составляющих системы «Университет» является подсистемой со своим составом. Поэтому для этих подсистем также можно построить свои модели состава. Разумеется, такой модели недостаточно для того, чтобы понять, как функционирует университет. И все-таки она дает более подробное представление об университете, чем модель «черного ящика».

Структурная модель системы

Структурную модель системы еще называют структурной схемой. На структурной схеме отражается состав системы и ее внутренние связи. Для отображения структурной схемы системы используются графы.

Граф состоит из вершин, обозначающих элементы системы, и ребер — линий, обозначающих связи (отношения) между элементами системы. Знакомая многим схема скоростного транспорта Москвы (рис. 1.4) является примером графа. Вершинами здесь являются станции метро, а ребрами — линии движения поездов. Такая схема позволяет пассажиру метро определить маршрут своего перемещения между любыми станциями. Схема метро отражает его радиально-кольцевую структуру.

Еще один пример графа показан на рис. 1.5. Это структурная модель молекулы углеводорода. Вершинами являются атомы водорода и углерода, ребра отображают валентные связи.

Связь между двумя станциями метро, соединенными линией движения, является двунаправленной, поскольку поезда могут двигаться в обе стороны. Валентная связь между атомами молекулы также не имеет выделенного направления. Такие графы называются неориентированными. Если же связь между двумя элементами системы действует только в одну сторону, то на графе она отображается направленной стрелкой. Такой граф называется ориентированным. Направленные линии связи на графе называются дугами.

На рис. 1.6 приведен пример ориентированного графа из области медицины. Известно, что у разных людей кровь может различаться по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы. Граф на рис. 1.6 показывает возможные варианты переливания крови. Группы крови — это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания крови одной группы человеку с другой группой. Например, из этого графа видно, что кровь I группы можно переливать любому человеку, а человек с I группой крови воспринимает кровь только своей группы. Видно также, что человеку с IV группой крови можно переливать любую кровь, но его кровь можно переливать только людям с той же группой.

На практике часто встречаются системы с иерархической структурой, граф которых называется деревом (рис. 1.7).

Дерево — это ориентированный граф, хотя при его изображении не всегда рисуются стрелки. Обычно вершины дерева располагаются по уровням сверху вниз. Дуги направлены от верхних вершин к нижним. Каждая вершина может быть связана с одной вершиной верхнего уровня (исходной) и множеством вершин нижнего уровня (порожденными). Такая связь называется «один ко многим». Единственная вершина самого верхнего уровня называется корнем дерева. Вершины самого нижнего уровня, у которых нет порожденных вершин, называются листьями дерева. Дерево является связным графом. Это значит, что между любыми двумя вершинами имеется хотя бы один путь, связывающий их между собой. В дереве отсутствуют петли — замкнутые траектории связей. Поэтому маршрут перемещения по дереву между любыми двумя вершинами всегда является единственным.

Структура организации файловой системы во внешней памяти компьютера является иерархической. Вершинами графа, отображающего файловую структуру, являются папки и файлы. Дуги отражают отношения вхождения одних вершин в другие. Дерево имеет многоуровневую структуру. Папка самого верхнего уровня называется корнем дерева. Конечные вершины такого дерева (листья) — это файлы и пустые папки.

Вопросы и задания

1. Какие существуют типы моделей систем? Чем они различаются?

2. Что такое граф? Из чего он состоит?

3. Какой граф называется неориентированным? Приведите примеры.

4. Какой граф называется ориентированным? Приведите примеры.

5. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения): дружат — Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша. Анализируя полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что тот станет известен кому-то другому?

6. Нарисуйте два варианта графа системы «Компьютер», содержащего следующие вершины: процессор, оперативная память, внешняя память, клавиатура, монитор, принтер:

а) линия связи обозначает отношение «передает информацию»;
б) линия связи обозначает отношение: «управляет».

Определение дерева

Деревом называется связный граф, который не содержит циклов.

Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.

Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.

Простым путем называется путь, в котором никакое ребро не встречается дважды.

Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:

Дерево — минимальный по числу рёбер связный граф.

Висячей вершиной называется вершина, из которой выходит ровно одно ребро.

Определения дерева:

1. Деревом называется связный граф не содержащий простых циклов.
2. Деревом называется связный граф, содержащий n вершин и n — 1 ребро.
3. Деревом называется связный граф, который при удалении любого ребра перестает быть связным.
4. Деревом называется граф, в котором любые две вершины соединены ровно одним простым путем.

Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.

Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.

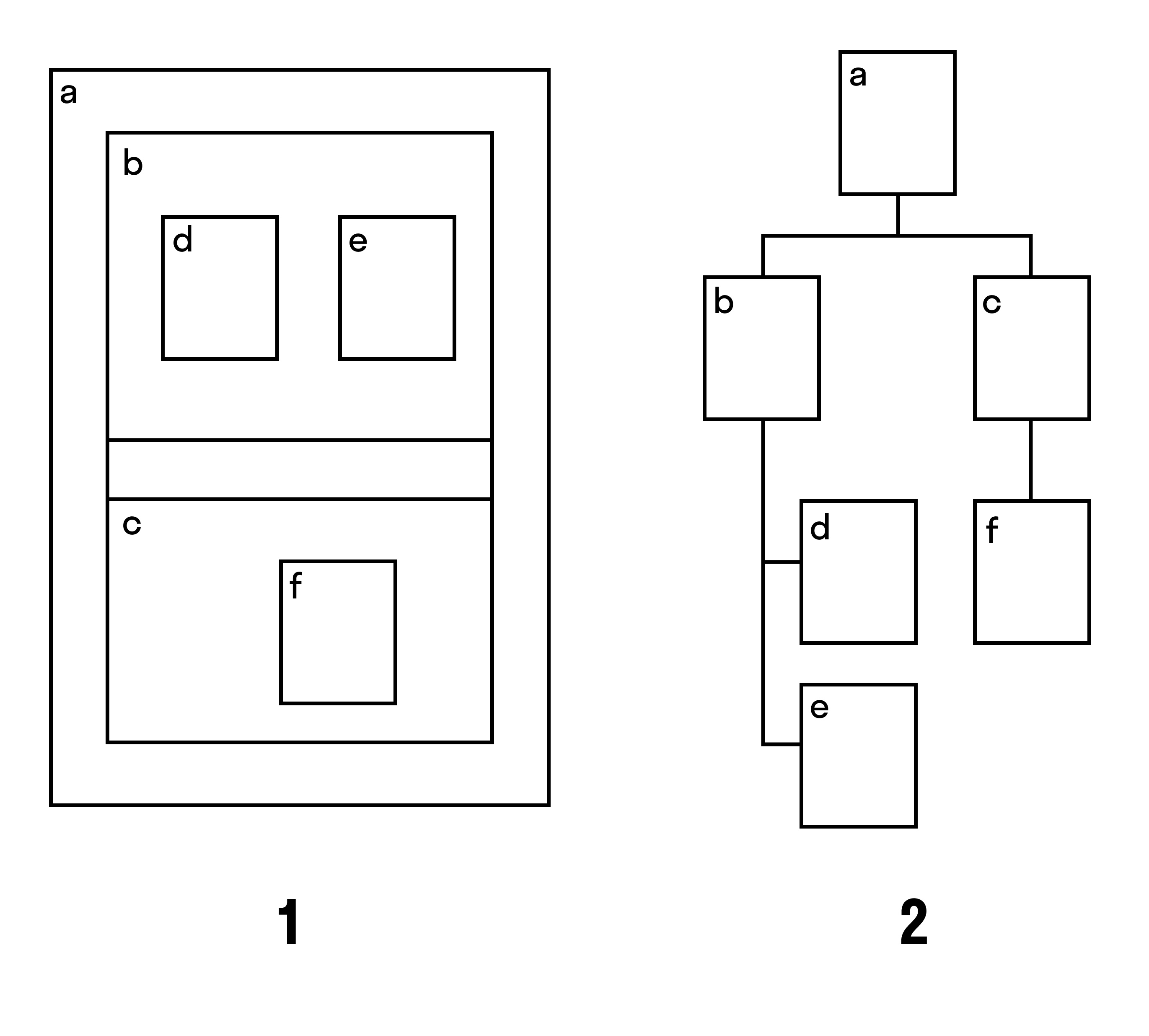
Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:

Теоремы дерева и их доказательства

В дереве с более чем одной вершиной есть висячая вершина.

Доказательство первой теоремы:

Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.

Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.

В дереве число вершин на 1 больше числа ребер.

Доказательство второй теоремы:

Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n < k мы доказали это факт. Найдём висячую вершину.

Граф, получающийся из исходного выкидыванием висячей вершины вместе с исходящим из нее ребром, очевидно, также является деревом — и в нём меньше на одну вершину и одно ребро. Значит для исходного графа также было верно доказываемое соотношение между количеством вершин и рёбер.

Верна и обратная теорема. Если в связном графе вершин на одну больше, чем ребер, то он является деревом.

Подграф называется остовным деревом, если он является деревом и множество его вершин совпадает с множеством вершин исходного графа.

У любого связного графа есть остовное дерево.

Доказательство третьей теоремы:

Чтобы найти остовное дерево графа G, можно найти цикл в графе G и выкинуть одно ребро цикла — потом повторить. И так пока в графе не останется циклов. Полученный граф будет связным, так как мы выкидывали рёбра, не нарушая связность, но в нём не будет циклов. Значит, он будет деревом.

Теория графов и современные прикладные задачи

На основе теории графов создали разные методы решения прикладных задач, в которых в виде графов можно моделировать сложные системы. В этих моделях узлы содержат отдельные компоненты, а ребра отражают связи между компонентами.

Графы и задача о потоках

Система водопроводных труб в виде графа выглядит так:

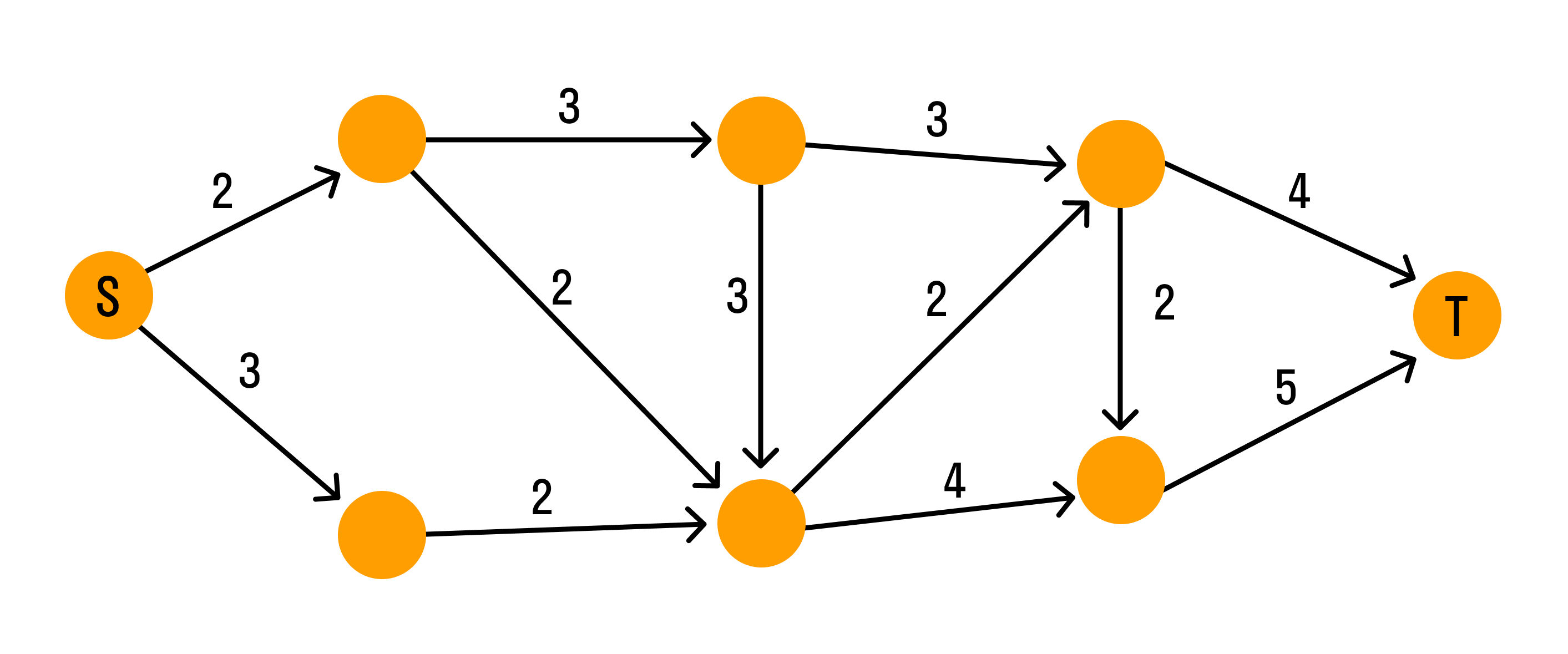
Каждая дуга графа отображает трубу. Числа над дугами (весы) — пропускная способность труб. Узлы — места соединения труб. Вода течёт по трубам только в одном направлении. Узел S — источник воды, узел T — сток.

Задача: максимизировать объём воды, протекающей от источника к стоку.

Для решения задачи о потоках можно использовать метод Форда-Фулкерсона. Идея метода в том, чтобы найти максимальный поток по шагам.

Сначала предполагают, что поток равен нулю. На каждом последующем шаге значение потока увеличивается, для чего ищут дополняющий путь, по которому поступает дополнительный поток. Эти шаги повторяют до тех пор, пока существуют дополнительные пути.

Задачу успешно применяют в различных распределенных системах: система электроснабжения, коммуникационная сеть, система железных дорог.

Графы и сетевое планирование

В задачах планирования сложных процессов, где много разных параллельных и последовательных работ, часто используют взвешенные графы. Их еще называют сетью ПЕРТ (PERT).

PERT (Program (Project) Evaluation and Review Technique) — техника оценки и анализа программ (проектов), которую используют при управлении проектами.

Сеть ПЕРТ — взвешенный ациклический ориентированный граф, в котором каждая дуга представляет работу (действие, операцию), а вес дуги — время, которое нужно на ее выполнение.

Если в сети есть дуги (a, b) и (b, c), то работа, представленная дугой (a, b), должна быть завершена до начала выполнения работы, представленной дугой (b, c). Каждая вершина (vi) представляет момент времени, к которому должны быть завершены все работы, задаваемые дугами, оканчивающимися в вершине (vi).

• одна вершина, у которой нет предшественников, определяет время начала работы
• одна вершина без последователей соответствует моменту завершения комплекса работ.

Путь максимальной длины между этими вершинами графа называется критическим путем. Чтобы выполнить всю работу быстрее, нужно найти задачи на критическом пути и придумать, как их выполнить быстрее. Например, нанять больше людей, перепридумать процесс или ввести новые технологии.