Цвет любого пиксела растрового изображения запоминается в компьютере с помощью комбинации битов

Как закодировать рисунок двоичным кодом

Рисунок состоит из линий и закрашенных областей. В идеале нам нужно закодировать все особенности этого изображения так, чтобы его можно было в точности восстановить из кода (например, распечатать на принтере).

И линия, и область состоят из бесконечного числа точек. Цвет каждой из этих точек нам нужно как-то закодировать. Так как точек бесконечно много, для этого нужно бесконечно много памяти, поэтому таким способом изображение закодировать не удастся. Однако «поточечную» идею всё-таки можно использовать.

Начнём с чёрно-белого рисунка. Представим себе, что на изображение ромба наложена сетка, которая разбивает его на квадратики. Такая сетка называется растром. Теперь каждый квадратик внутри ромба зальём чёрным цветом, а каждый квадратик вне ромба — белым. Для тех квадратиков, в которых часть оказалась закрашена чёрным цветом, а часть — белым, выберем цвет в зависимости от того, какая часть (чёрная или белая) больше (рис. 2.19).

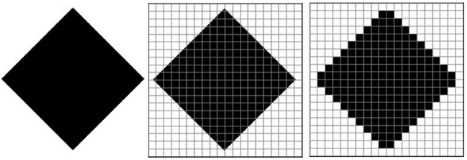
У нас получился растровый рисунок, состоящий из квадратиков-пикселей.

Пиксель (англ. pixel: picture element — элемент рисунка) — это наименьший элемент рисунка, для которого можно задать свой цвет.

Разбив рисунок на квадратики, мы выполнили его дискретизацию. Действительно, у нас был непрерывный рисунок — изображение ромба. В результате мы получили дискретный объект — набор пикселей.

Двоичный код для чёрно-белого рисунка, полученного в результате дискретизации, можно построить следующим образом:

1) кодируем белые пиксели нулями, а чёрные — единицами 1) ;
2) выписываем строки полученной таблицы одну за другой.

1) Можно сделать и наоборот, чёрные пиксели обозначить нулями, а белые — единицами.

Покажем это на простом примере (рис. 2.20).

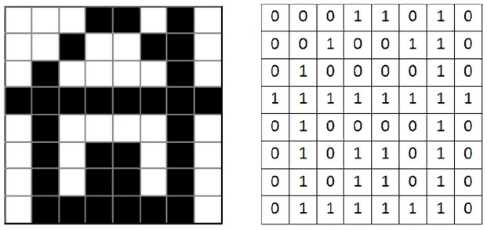
Ширина этого рисунка — 8 пикселей, поэтому каждая строка таблицы состоит из 8 двоичных разрядов — битов. Чтобы не писать очень длинную цепочку нулей и единиц, удобно использовать шестнадцатеричную систему счисления, закодировав 4 соседних бита (тетраду) одной шестнадцатеричной цифрой. Например, для первой строки получаем код 1А₁₆:

а для всего рисунка: 1A2642FF425A5A7E₁₆.

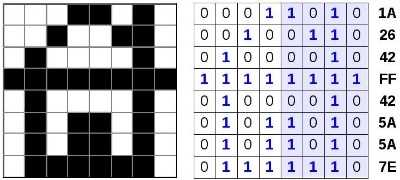
Используя полученный шестнадцатеричный код картинки, подсчитайте её информационный объём в битах и байтах.

Очень важно понять, что мы приобрели и что потеряли в результате дискретизации. Самое главное — мы смогли закодировать изображение в двоичном коде. Однако при этом рисунок исказился — вместо ромба мы получили набор квадратиков. Причина искажения в том, что в некоторых квадратиках части исходного рисунка были закрашены разными цветами, а в закодированном изображении каждый пиксель обязательно имеет один цвет. Таким образом, часть исходной информации при кодировании была потеряна. Это проявится, например, при увеличении рисунка — квадратики увеличиваются и рисунок ещё больше искажается. Чтобы уменьшить потери информации, нужно уменьшать размер пикселя, т. е. увеличивать разрешение.

Разрешение — это количество пикселей, приходящихся на единицу линейного размера изображения (чаще всего — на 1 дюйм).

Разрешение обычно измеряется в пикселях на дюйм (используется английское обозначение ppi: — pixels per inch). Например, разрешение 254 ppi означает, что на дюйм приходится 254 пикселя.

Чем больше разрешение, тем точнее кодируется рисунок (меньше информации теряется), однако одновременно растёт и объём файла.

Одна и та же картинка была отсканирована дважды: в первый раз с разрешением 300 ppi, а второй раз — с разрешением 600 ppi. Что можно сказать о размерах полученных файлов?

Существуют два основных способа получения растровых изображений:

1) ввод с помощью какого-либо устройства, например сканера, цифрового фотоаппарата или веб-камеры; напомним, что при сканировании происходит преобразование информации в компьютерные данные (оцифровка);

2) создание рисунка с помощью какой-либо программы.

Используя дополнительные источники, найдите ответы на вопросы.

— Чему равен один дюйм в миллиметрах?
— Если отсканировать рисунок с разрешением 254 ppi, какой размер будет иметь изображение одного пикселя?
— Какие размеры в пикселях будет иметь изображение рисунка размером 10 х 15 см, если отсканировать его с разрешением 254 ppi?

Следующая страница Как кодируется цвет?

Cкачать материалы урока

Двоичное кодирование информации.

Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр 0 и 1. Эти два символа принято называть двоичными цифрами или битами. С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.

Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.

Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.

Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.

Система счисления	Основание	Алфавит цифр
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двоичная	2	0, 1
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.

Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой.

Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используются не 10 цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным.

Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.

Переведем десятичное число 20 в двоичную систем счисления (основание системы счисления p=2).

В итоге получили 20₁₀ = 10100₂.

Двоичное кодирование текстовой информации

Начиная с 60-х годов, компьютеры все больше стали использовать для обработки текстовой информации и в настоящее время большая часть ПК в мире занято обработкой именно текстовой информации.

Традиционно для кодирования одного символа используется количество информации = 1 байту (1 байт = 8 битов).

Для кодирования одного символа требуется один байт информации.

Учитывая, что каждый бит принимает значение 1 или 0, получаем, что с помощью 1 байта можно закодировать 256 различных символов. (28 = 256)

Кодирование заключается в том, что каждому символу ставится в соответствие уникальный двоичный код от 00000000 до 11111111 (или десятичный код от 0 до 255).

Важно, что присвоение символу конкретного кода – это вопрос соглашения, которое фиксируется кодовой таблицей.

Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера (коды), называется таблицей кодировки.

Создавать и хранить графические объекты в компьютере можно двумя способами – как растровое или как векторное изображение. Для каждого типа изображений используется свой способ кодирования.

Кодирование растровых изображений

Растровое изображение представляет собой совокупность точек (пикселей) разных цветов. Пиксель – минимальный участок изображения, цвет которого можно задать независимым образом.

В процессе кодирования изображения производится его пространственная дискретизация. Пространственную дискретизацию изображения можно сравнить с построением изображения из мозаики (большого количества маленьких разноцветных стекол). Изображение разбивается на отдельные маленькие фрагменты (точки), причем каждому фрагменту присваивается значение его цвета, то есть код цвета (красный, зеленый, синий и так далее).

Для черно-белого изображения информационный объем одной точки равен одному биту (либо черная, либо белая – либо 1, либо 0).

Для четырех цветного – 2 бита.

Для 8 цветов необходимо – 3 бита.

Для 16 цветов – 4 бита.

Для 256 цветов – 8 бит (1 байт).

Качество изображения зависит от количества точек (чем меньше размер точки и, соответственно, больше их количество, тем лучше качество) и количества используемых цветов (чем больше цветов, тем качественнее кодируется изображение). Растровые изображения очень чувствительны к масштабированию (увеличению или уменьшению). При уменьшении растрового изображения несколько соседних точек преобразуются в одну, поэтому теряется различимость мелких деталей изображения. При увеличении изображения увеличивается размер каждой точки и появляется ступенчатый эффект, который можно увидеть невооруженным глазом.

Кодирование векторных изображений

Векторное изображение представляет собой совокупность графических примитивов (точка, отрезок, эллипс…). Каждый примитив описывается математическими формулами. Кодирование зависит от прикладной среды.

Достоинством векторной графики является то, что файлы, хранящие векторные графические изображения, имеют сравнительно небольшой объем.

Важно также, что векторные графические изображения могут быть увеличены или уменьшены без потери качества.

Объем видеопамяти

Объем необходимой видеопамяти определяется размером графической сетки дисплея и количеством цветов. Минимальный объем видеопамяти должен быть таким, чтобы в него помещался один кадр (одна страница) изображения. Например, для сетки 640 х 480 и черно-белого изображения минимальный объем видеопамяти должен быть таким:

640 • 480 • 1 бит = 307 200 битов = 38 400 байтов.

Это составляет 37,5 Кбайт.

Для работы с 256-цветной палитрой на мониторе с разрешением 1024 х 768 минимальный объем видеопамяти составляет 768 Кб.

На современных высококачественных дисплеях используется палитра более чем из 16 миллионов цветов (b = 24 бита). Требуемый объем видеопамяти в этом случае — несколько мегабайтов.

На самом деле видеопамять хранит одновременно не одно изображение экрана, а множество. Это способствует быстрой смене кадров. Поэтому размер видеопамяти на современных ПК составляет от сотен мегабайтов до нескольких гигабайтов.

О сжатии растровой графики

Иногда характеристики растрового изображения записывают в такой форме: 1024x768x24. Это означает, что ширина изображения равна 1024 пикселям, высота – 768 и глубина цвета равна 24. 1024×768 – рабочее разрешение для 15 – 17 дюймовых мониторов. Несложно догадаться, что размер несжатого изображения с такими параметрами будет равен 1024*768*24 = 18874368 байт. Это более 18 мегабайт – слишком много для одной картинки, особенно если требуется хранить несколько тысяч таких картинок – это не так уж много по компьютерным меркам. Вот почему компьютерную графику используют почти всегда в сжатом виде.

RLE (Run Length Encoding) – метод сжатия, заключающийся в поиске последовательностей одинаковых пикселей в сточках растрового изображения («красный, красный, . красный» записывается как «N красных»).

LZW (Lempel–Ziv–Welch) – более сложный метод, ищет повторяющиеся фразы – одинаковые последовательности пикселей разного цвета. Каждой фразе ставится в соответствие некоторый код, при расшифровке файла код замещается исходной фразой.

При сжатии файлов формата JPEG (с потерей качества) изображение разбивается на участки 8×8 пикселей, и в каждом участке их значение усредняется. Усреднённое значение располагается в левом верхнем углу блока, остальное место занимается меньшими по яркости пикселями. Затем большинство пикселей обнуляются. При расшифровке нулевые пиксели получают одинаковый цвет. Затем к изображению применяется алгоритм Хаффмана.

Алгоритм Хаффмана основан на теории вероятности. Сначала элементы изображения (пиксели) сортируются по частоте встречаемости. Затем из них строится кодовое дерево Хаффмана. Каждому элементу сопоставляется кодовое слово. При стремлении размера изображения к бесконечности достигается максимальность сжатия. Этот алгоритм также используется в архиваторах.

Сжатие применяется и для векторной графики, но здесь уже нет таких простых закономерностей, так как форматы векторных файлов достаточно сильно различаются по содержанию.

О сжатии растровой графики

15.4. Цветовая модель RGB

Для синтеза цвета на экранах компьютеров, телевизоров, смартфонов и других устройств отображения графической информации выбраны красный, зелёный и синий цвета. Смешением трёх основных цветов синтезируются все остальные цвета. Такая модель называется аддитивной (аддитивный — получаемый путём сложения, от лат. additio — прибавление).

Выбор этих цветов неслучаен и кроется в физиологии человеческого зрения. Действительно, в сетчатке глаза человека есть три типа колбочек, максимумы чувствительности которых приходятся на красный, зелёный и синий участки спектра (табл. 3.12).

Таблица 3.12

Спектральная чувствительность человеческого глаза

Модель RGB (рис. 3.8) определяет пространство цветов в виде единичного куба с осями R (красная компонента), G (зелёная компонента), В (синяя компонента).

Рассмотрим эту модель подробно.

1. Любая точка куба (r; g; b) определяет некоторый цвет.

2. Точка (0; 0; 0) соответствует чёрному цвету; точка (1; 1; 1) соответствует белому цвету; линия (0; 0; 0)-(1; 1; 1) описывает все градации серого от чёрного до белого.

Рис. 3.8. Цветовой куб для RGB-кодирования

3. При движении по прямой от точки (0; 0; 0) к точке (r; g; b) получаем все градации яркости цвета (r; g; b) — от самого тёмного до самого яркого.

4. На гранях куба (r = 0), (g = 0) и (b = 0) расположены самые насыщенные цвета. Чем ближе точка к главной диагонали (0; 0; 0)—(1; 1; 1), тем менее насыщен соответствующий цвет. Если все три координаты точки (r; g; b) ненулевые, то цвет — ненасыщенный.

Мы уже упоминали о квантовании. Благодаря ему в компьютере интенсивность цветовых компонент определяется не вещественными (из интервала [0; 1]), а целыми числами. Для этого «единичные» отрезки на «красной», «зелёной» и «синей» осях разбивают на несколько поддиапазонов, каждый из которых получает свой номер. Цвет пикселя изображения, которое будет выведено на экран, задаётся тремя целыми неотрицательными числами — номерами поддиапазонов, в которые «попадает» этот цвет. Качество цветопередачи зависит от количества выделяемых поддиапазонов.

В современных компьютерах для сохранения информации о цвете каждой точки цветного изображения в модели RGB обычно отводится 3 (режим True Color) или 2 (режим High Color) байта.

В первом случае на кодирование градаций яркости каждого из основных цветов отводится 1 байт: код 00000000 (00) показывает, что данной составляющей нет вообще, код 11111111 (FF) соответствует наибольшей интенсивности соответствующей цветовой компоненты. Всего можно закодировать 256 (от 0 до 255) градаций яркости каждой цветовой компоненты, что обеспечивает возможность представления 256 • 2256 • 256 = 2 8+8+8 = 2 24 = 16 777 216 цветов. Человеческий глаз не может различить большего разнообразия цветов. Это позволяет считать видеорежим True Color (истинный цвет) абсолютно соответствующим цветам реального мира.

В режиме High Color цвет каждой точки кодируется 16 битами. На кодирование красной и синей составляющих при этом отводится по 5 бит, на кодирование зелёной составляющей — 6 бит. Пять бит позволяют представить по 32 градации яркости красного и синего цветов. Поскольку человеческий глаз наиболее чувствителен к зелёной составляющей цвета, под её шкалу отведено 6 бит, что позволяет сохранить 64 градации яркости этого цвета. Всего в рассматриваемом режиме можно представить 2 5+6+5 = 2 16 = 65 536 цветов. Цвета изображений, сохранённых в режиме High Color также вполне реалистичны и «комфортны» для человеческого глаза. При этом размеры соответствующих файлов в 1,5 раза меньше, чем при использовании режима True Color.

Глубина цвета (i) — количество бит, используемое для хранения и представления цвета при кодировании одного пикселя растровой графики или видеоизображения.

Палитра (N) — количество цветов, которые могут быть использованы для воспроизведения изображения.

Справедливо соотношение: N = 2 i .
Пример. Имеется канал связи, обеспечивающий передачу информации со скоростью 16 000 бит/с. Выясним, сколько секунд потребуется для передачи по этому каналу 256-цветного растрового изображения размером 800 х 600 пикселей.

Зная палитру — количество цветов, используемых для воспроизведения изображения, вычислим глубину цвета — количество бит для представления цвета одного пикселя.

256 = 2 i , i = 8 (бит).

Размер файла с изображением равен: 800 • 600 • 8 (бит).

Вычислим время передачи данного файла:

Кодирование цвета

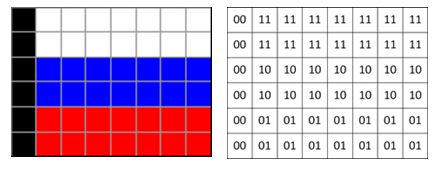
Что делать, если рисунок цветной? В этом случае для кодирования цвета пикселя уже не обойтись одним битом. Например, в показанном на рисунке изображении российского флага $4$ цвета: черный, синий, красный и белый. Для кодирования одного из четырех вариантов нужно $2$ бита, поэтому код каждого цвета (и код каждого пикселя) будет состоять из двух бит. Пусть

Кодирование с палитрой

Как правило, чем меньше цветов используется, тем больше будет искажаться цветное изображение. Таким образом, при кодировании цвета тоже есть неизбежная потеря информации, которая «добавляется» к потерям, вызванным дискретизацией. Очень часто (например, в схемах, диаграммах и чертежах) количество цветов в изображении невелико (не более $256$). В этом случае применяют кодирование с палитрой.

Цветовая палитра – это таблица, в которой каждому цвету, заданному в виде составляющих в модели RGB, сопоставляется числовой код.

Кодирование с палитрой выполняется следующим образом:

выбираем количество цветов $N$ (как правило, не более $256$);
из палитры истинного цвета ($16 777 216$ цветов) выбираем любые $N$ цветов и для каждого из них находим составляющие в модели RGB;
каждому из цветов присваиваем номер (код) от

Достоинства и недостатки растрового кодирования

Растровое кодирование имеет достоинства:
- универсальный метод (можно закодировать любое изображение);
- единственный метод для кодирования и обработки размытых изображений, не имеющих четких границ, например, фотографий.
И недостатки:
- при дискретизации всегда есть потеря информации;
- при изменении размеров изображения искажается цвет и форма объектов на рисунке, поскольку при увеличении размеров надо как-то восстановить недостающие пиксели, а при уменьшении – заменить несколько пикселей одним;
- размер файла не зависит от сложности изображения, а определяется только разрешением и глубиной цвета.
Как правило, растровые рисунки имеют большой объем.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 14.04.2016

Анастасия Николаевна Королева

Эксперт по предмету «Информатика»

Автор24 — это сообщество учителей и преподавателей, к которым можно обратиться за помощью с выполнением учебных работ.

$ до $N–1$;
составляем палитру, записывая сначала RGB-составляющие цвета, имеющего код $, затем составляющие цвета с кодом $1$ и т.д.

Цвет каждого пикселя кодируется не в виде значений RGB-составляющих, а как номер цвета в палитре. Например, при кодировании изображения российского флага (см. выше) были выбраны $4$ цвета:

черный: RGB-код (,0,0$); двоичный код $002$;
красный: RGB-код ($255,0,0$); двоичный код $012$;
синий: RGB-код (,0,255$); двоичный код $102$;
белый: RGB-код ($255,255,255$); двоичный код $112$.

Поэтому палитра, которая обычно записывается в специальную служебную область в начале файла (ее называют заголовком файла), представляет собой четыре трехбайтных блока:

Код каждого пикселя занимает всего два бита.

Палитры с количеством цветом более $256$ на практике не используются.

$ обозначает черный цвет, $01$ – красный, $10$ – синий и $11$ – белый. Тогда получаем такую таблицу:

Проблема только в том, что при выводе на экран нужно как-то определить, какой цвет соответствует тому или другому коду. То есть информацию о цвете нужно выразить в виде числа (или набора чисел).

Человек воспринимает свет как множество электромагнитных волн. Определенная длина волны соответствуют некоторому цвету. Например, волны длиной $500-565$ нм – это зеленый цвет. Так называемый «белый» свет на самом деле представляет собой смесь волн, длины которых охватывают весь видимый диапазон.

Согласно современному представлению о цветном зрении (теории Юнга-Гельмгольца), глаз человека содержит чувствительные элементы трех типов. Каждый из них воспринимает весь поток света, но первые наиболее чувствительны в области красного цвета, вторые – области зеленого, а третьи – в области синего цвета. Цвет – это результат возбуждения всех трех типов рецепторов. Поэтому считается, что любой цвет (то есть ощущения человека, воспринимающего волны определенной длины) можно имитировать, используя только три световых луча (красный, зеленый и синий) разной яркости. Следовательно, любой цвет приближенно раскладывается на три составляющих – красную, зеленую и синюю. Меняя силу этих составляющих, можно составить любые цвета. Эта модель цвета получила название RGB по начальным буквам английских слов red (красный), green (зеленый) и blue (синий).

В модели RBG яркость каждой составляющей (или, как говорят, каждого канала) чаще всего кодируется целым числом от $ до $255$. При этом код цвета – это тройка чисел (R,G,B), яркости отдельных каналов. Цвет (,0,0$) – это черный цвет, а ($255,255,255$) – белый. Если все составляющие имеют равную яркость, получаются оттенки серого цвета, от черного до белого.

Чтобы сделать светло-красный (розовый) цвет, нужно в красном цвете ($255,0,0$) одинаково увеличить яркость зеленого и синего каналов, например, цвет ($255, 150, 150$) – это розовый. Равномерное уменьшение яркости всех каналов делает темный цвет, например, цвет с кодом ($100,0,0$) – тёмно-красный.

Всего есть по $256$ вариантов яркости каждого из трех цветов. Это позволяет закодировать $256^3= 16 777 216$ оттенков, что более чем достаточно для человека. Так как $256 = 2^8$, каждая из трех составляющих занимает в памяти $8$ бит или $1$ байт, а вся информация о каком-то цвете – $24$ бита (или $3$ байта). Эта величина называется глубиной цвета.

Глубина цвета – это количество бит, используемое для кодирования цвета пикселя.

$24$-битное кодирование цвета часто называют режимом истинного цвета (англ. True Color – истинный цвет). Для вычисления объема рисунка в байтах при таком кодировании нужно определить общее количество пикселей (перемножить ширину и высоту) и умножить результат на $3$, так как цвет каждого пикселя кодируется тремя байтами. Например, рисунок размером $20×30$ пикселей, закодированный в режиме истинного цвета, будет занимать $20×30×3 = 1800$ байт.

Кроме режима истинного цвета используется также $16$-битное кодирование (англ. High Color – «высокий» цвет), когда на красную и синюю составляющую отводится по $5$ бит, а на зеленую, к которой человеческий глаз более чувствителен – $6$ бит. В режиме High Color можно закодировать $2^ = 65 536$ различных цветов. В мобильных телефонах $12$-битное кодирование цвета ($4$ бита на канал, $4096$ цветов).