Урок 13Представление текстов в памяти компьютера. Кодировочные таблицы

Представление элементарных данных в ОЗУ

Как уже сказано, различными типами элементарных данных являются символы, целые числа, вещественные числа и логические данные. Логический и физический уровни их представления определяются конструктивными особенностями ОЗУ компьютера. В частности, поскольку память компьютера имеет байтовую структуру, к ней привязывается представление любых данных. Более точным является утверждение, что для представления значений элементарных данных в памяти компьютера используется машинное слово; этот термин в информатике применяется в двух значениях:

Машинное слово — (1) совокупность двоичных элементов, обрабатываемая как единое целое в устройствах и памяти компьютера;

(2) данные, содержащиеся в одной ячейке памяти компьютера.

С технической точки зрения машинное слово объединяет запоминающие элементы, служащие для записи 1 бит информации, в единую ячейку памяти. Количество таких объединяемых элементов кратно 8, т.е. целому числу байт. Например, в отечественной ЭВМ БЭСМ-6 длина машинного слова составляла 48 бит (6 байт), в машинах СМ и IBM — 16 бит (2 байта). Доступ к машинному слову в операциях записи и считывания осуществляется по номеру ячейки памяти, который называется адресом ячейки.

Запоминающие устройства, в которых доступ к данным осуществляется по адресу ячейки, где они хранятся, называются устройствами с произвольным доступом.*

* Именно по этой причине в англоязычной литературе вместо ОЗУ используется термин RAM – Random Access Memory — «память с произвольной выборкой».

Время поиска нужной ячейки, а также продолжительность операций считывания или записи в ЗУ произвольного доступа одинаково для всех ячеек независимо от их адреса.

Для логического уровня важно то, что представление значений любых элементарных данных должно быть ориентировано на использование машинных слов определенной и единой для данного компьютера длины, поскольку их представление на физическом уровне производится именно в ячейках ОЗУ (на ВЗУ элементарные данные в качестве самостоятельных не представляются и доступ к ним отсутствует).

Рассмотрим особенности представления всех типов элементарных данных с помощью 16-битного машинного слова. Порядок размещения значений данных представлен на рис.6.1.

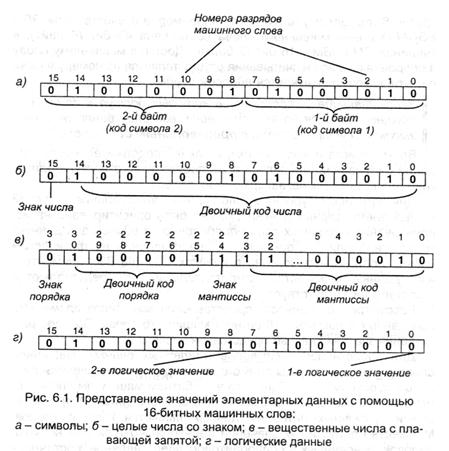
Для представления символов (литерных данных) машинное слово делится на группы по 8 бит, в которые и записываются двоичные коды символов. Ясно, что в 16-битном машинном слове могут быть записаны одновременно два символа (рис. 6.1,а). Значениями одиночных литерных данных являются коды символов. Множество допустимых значений данных этого типа для всех кодировок, основанных на однобайтовом представлении, составляет 2 8 — 256; двубайтовая кодировка Unicode допускает 65536 значений. Совокупность символов образует алфавит, т.е. для них установлен лексикографический порядок следования в соответствии с числовым значением кода; это, в свою очередь, позволяет определить над множеством символьных данных операции математических отношений >,

В представлении целых чисел со знаком (например, тип Integer в языке PASCAL) старший бит (15-й), как уже обсуждалось ранее, отводится под запись знака числа (0 соответствует «+», 1 — «-»), а остальные 15 двоичных разрядов — под запись прямого (для положительного) или обратного (для отрицательного) двоичного кода числа (рис. 6.1,6). При этом возможные значения чисел ограничены интервалом [-32768 + 32767]. Наряду с описанным используется и другой формат представления целых чисел — беззнаковый; очевидно, он применим только для записи положительных чисел. В этом случае под запись числа отводятся все 16 двоичных разрядов, и интервал разрешенных значений оказывается [0 * 65535] (в PASCAL’e такой числовой тип называется Word). Помимо математических отношений над целыми числами определены операции сложения, вычитания и умножения (в тех случаях, когда они не приводят к переполнению разрядной сетки), а также целочисленного деления и нахождения остатка от целочисленного деления.

Значения элементарных данных формируются в ходе исполнения программы и имеют физическое представление в ОЗУ. В отличие от них идентификаторы данных существуют только на уровне логического представления — они используются для обозначения данных в тексте программы, однако при трансляции программы с языка программирования в машинный код имена заменяются номерами ячеек, в которых данные размещаются. При исполнении такой программы обращение к данным производится по адресу ячейки, а не идентификатору. Адреса могут быть абсолютными — в этом случае они не изменяются при загрузке программы в ОЗУ — именно такой способ адресации применяется в исполняемых программных файлах с расширением сот. Однако в силу некоторых особенностей распределения памяти компьютера размер таких программ не может превышать 64 Кб. В исполняемых файлах с расширением ехе на этапе трансляции устанавливаются относительные адреса данных, которые конкретизируются при размещении программы в ОЗУ — это несколько замедляет начало исполнения, зато снимает указанное выше ограничение на размер программы.

В заключение следует заметить, что в некоторых прикладных программах в качестве элементарных используются и другие типы данных, например, тип «Data» или «Денежный» в MS Excel и MS Access. Однако они являются самостоятельными только для пользователя программы; самой же программой они сводятся к некоторой комбинации рассмотренных выше элементарных данных.

Как представляются тексты в памяти компьютера

А теперь «заглянем» в память компьютера и разберемся, как же представлена в нем текстовая информация.

Текстовая информация состоит из символов: букв, цифр, знаков препинания, скобок и др. Мы уже говорили, что множество всех символов, с помощью которых записывается текст, называется алфавитом, а число символов в алфавите — его мощностью.

Широко распространенным способом представления текстовой информации в компьютере является использование алфавита мощностью 256 символов. Один символ такого алфавита несет 8 битов информации: 2 8 = 256. 8 битов = 1 байт, следовательно (см. § 6):

Двоичный код каждого символа занимает 1 байт памяти компьютера.

Теперь возникает вопрос, какой именно восьмиразрядный двоичный код поставить в соответствие тому или иному символу. (Понятно, что это дело условное, можно придумать множество способов кодирования.)

Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код — порядковый номер символа в двоичной системе счисления.

Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.

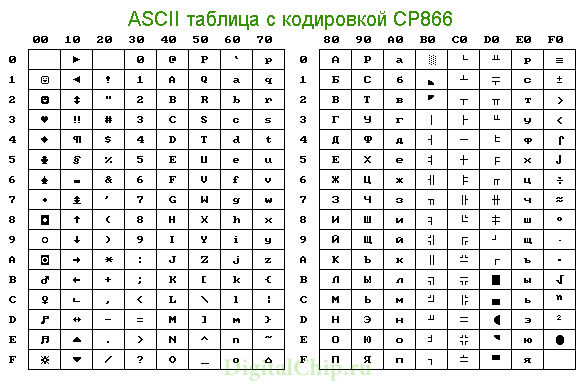
На ЭВМ первых поколений для разных типов машин использовались различные таблицы кодировки. С распространением персональных компьютеров типа IBM PC международным стандартом стала таблица кодировки под названием ASCII (American Standart Code for Information Interchange — американский стандартный код для обмена информацией). Точнее говоря, стандартной в этой таблице является только первая половина, т. е. символы с номерами от нуля (двоичный код 00000000) до 127(01111111). Сюда входят буквы латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы. Остальные 128 кодов, ОТ 10000000 до 11111111, составляют так называемую кодовую страницу. Например, кодовая страница номер 1251 (СР1251) содержит русский алфавит и используется в операционной системе Windows и ее приложениях. Таблицу кодировки, используемую в Windows, называют ANSI (American National Standart Institute -^Американский национальный институт стандартов). Первые половины таблиц ASCII и ANSI полностью совпадают.

В таблице 3.1 приведена стандартная часть кода ANSI (коды от 0 до 31 имеют особое назначение, не отражаются какими-либо знаками и в данную таблицу не включены). Здесь приведены десятичные номера символов, символы, двоичные коды.

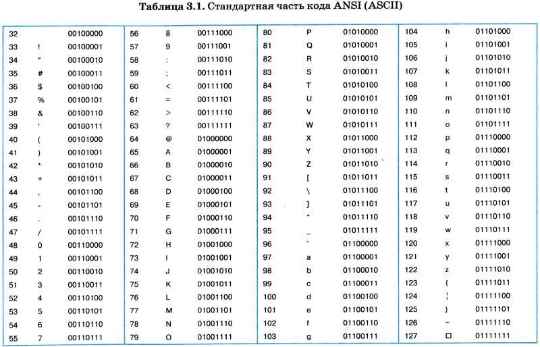
Обратите внимание на то, что в этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.

Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:

01100110 01101001 01101100 01100101.

А теперь попробуйте решить обратную задачу. Какое слово записано следующим двоичным кодом:

01100100 01101001 01110011 01101011?

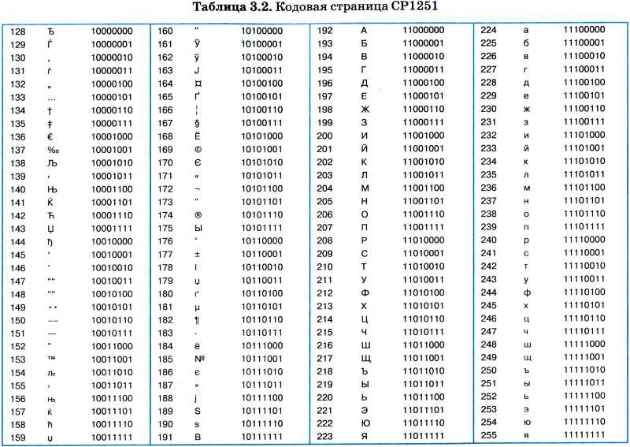
В таблице 3.2 приведена кодовая страница СР1251. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования. Однако это правило действует не во всех существующих кодовых страницах с русским алфавитом.

Помимо восьмиразрядной кодировки символов все большее распространение получает шестнадцатиразрядная — двухбайтовая кодировка. Международный стандарт такой кодировки носит название UNICODE.

Тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные нам буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.

Из памяти компьютера текст может быть выведен на экран или на печать в символьной форме. Но для долговременного хранения его следует записать на внешний носитель в виде файла.

Представление целых чисел в дополнительном коде

Другой способ представления целых чисел — дополнительный код . Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer (все названия типов данных здесь и ниже представлены в том виде, в каком они приняты в языке программирования Turbo Pascal. В других языках такие типы данных тоже есть, но могут иметь другие названия) лежат в диапазоне от -32768 (-2 15 ) до 32767 (2 15 — 1) и для их хранения отводится 2 байта (16 бит); типа LongInt — в диапазоне от -2 31 до 2 31 — 1 и размещаются в 4 байтах (32 бита); типа Word — в диапазоне от 0 до 65535 (2 16 — 1) (используется 2 байта) и т.д.

Как видно из примеров, данные могут быть интерпретированы как числа со знаком , так и без знака . В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если — единицу.

Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

Дополнительный код положительного числа совпадает с его прямым кодом . Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число.

Например, если число 37 (10) = 100101 (2) объявлено величиной типа Integer ( шестнадцатибитовое со знаком ), то его прямым кодом будет 0000000000100101, а если величиной типа LongInt ( тридцатидвухбитовое со знаком ), то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричное представление кода. Полученные коды можно переписать соответственно как 0025 (16) и 00000025 (16) .

Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:

1. записать прямой код модуля числа;
2. инвертировать его (заменить единицы нулями, нули — единицами);
3. прибавить к инверсному коду единицу.

Например, запишем дополнительный код числа -37, интерпретируя его как величину типа LongInt (тридцатидвухбитовое со знаком):

1. прямой код числа 37 есть 00000000000000000000000000100101;
2. инверсный код 11111111111111111111111111011010;
3. дополнительный код 11111111111111111111111111011011 или FFFFFFDB₍₁₆₎.

При получении числа по его дополнительному коду прежде всего необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:

1. вычесть из кода числа 1;
2. инвертировать код;
3. перевести в десятичную систему счисления. Полученное число записать со знаком минус.

Примеры. Запишем числа, соответствующие дополнительным кодам:

1. 0000000000010111. Поскольку в старшем разряде записан нуль, то результат будет положительным. Это код числа 23.
2. 1111111111000000. Здесь записан код отрицательного числа. Исполняем алгоритм: 1) 1111111111000000₍₂₎ — 1₍₂₎ = 1111111110111111₍₂₎; 2) 0000000001000000; 3) 1000000₍₂₎ = 64₍₁₀₎.
   Ответ: -64.

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Информатика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Информатика — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений.

Как закодировать все используемые на компьютере алфавиты?

Для ответа на этот вопрос пойдем историческим путем.

В 60-х годах XX века в американском национальном институте стандартизации (ANSI)была разработана таблица кодирования символов, которая впоследствии была использована во всех операционных системах. Эта таблица называется ASCII (American Standard Code for Information Interchange – американский стандартный код для обмена информацией). Чуть позже появилась расширенная версия ASCII.

В соответствие с таблицей кодирования ASCII для представления одного символа выделяется 1 байт (8 бит). Набор из 8 ячеек может принять 2 8 = 256 различных значений. Первые 128 значений (от 0 до 127) постоянны и формируют так называемую основную часть таблицы, куда входят десятичные цифры, буквы латинского алфавита (заглавные и строчные), знаки препинания (точка, запятая, скобки и др.), а также пробел и различные служебные символы (табуляция, перевод строки и др.). Значения от 128 до 255 формируют дополнительную часть таблицы, где принято кодировать символы национальных алфавитов.

Представление данных в памяти персонального компьютера (числа, символы, графика, звук).

Воспринимая информацию с помощью органов чувств, человек стремится зафиксировать ее так, чтобы она стала понятной и другим, представляя ее в той или иной форме.

Музыкальную тему композитор может наиграть на пианино, а затем записать с помощью нот. Образы, навеянные все той же мелодией, поэт может воплотить в виде стихотворения, хореограф выразить танцем, а художник — в картине.

Человек выражает свои мысли в виде предложений, составленных из слов. Слова, в свою очередь, состоят из букв. Это — алфавитное представление информации.

Форма представления одной и той же информации может быть различной. Это зависит от цели, которую вы перед собой поставили. С подобными операциями вы сталкиваетесь на уроках математики и физики, когда представляете решение в разной форме. Например, решение задачи: «Найти значение математического выражения . » можно представить в табличной или графической форме. Для этого вы пользуетесь визуальными средствами представления информации: числами, таблицей, рисунком.

Таким образом, информацию можно представить в различной форме:

знаковой письменной, состоящей из различных знаков, среди которых принято выделять

символьную в виде текста, чисел, специальных символов (например, текст учебника);

графическую (например, географическая карта);

табличную (например, таблица записи хода физического эксперимента);

в виде жестов или сигналов (например, сигналы регулировщика дорожного движения);

устной словесной (например, разговор).

Форма представления информации очень важна при ее передаче: если человек плохо слышит, то передавать ему информацию в звуковой форме нельзя; если у собаки слабо развито обоняние, то она не может работать в розыскной службе. В разные времена люди передавали информацию в различной форме с помощью: речи, дыма, барабанного боя, звона колоколов, письма, телеграфа, радио, телефона, факса.

Независимо от формы представления и способа передачи информации, она всегда передается с помощью какого-либо языка.

На уроках математики вы используете специальный язык, в основе которого — цифры, знаки арифметических действий и отношений. Они составляют алфавит языка математики.

На уроках физики при рассмотрении какого-либо физического явления вы используете характерные для данного языка специальные символы, из которых составляете формулы. Формула — это слово на языке физики.

На уроках химии вы также используете определенные символы, знаки, объединяя их в «слова» данного языка.

Существует язык глухонемых, где символы языка — определенные знаки, выражаемые мимикой лица и движениями рук.

Основу любого языка составляет алфавит — набор однозначно определенных знаков (символов), из которых формируется сообщение.

Языки делятся на естественные (разговорные) и формальные. Алфавит естественных языков зависит от национальных традиций. Формальные языки встречаются в специальных областях человеческой деятельности (математике, физике, химии и т. д.). В мире насчитывается около 10000 разных языков, диалектов, наречий. Многие разговорные языки произошли от одного и того же языка. Например, от латинского языка образовались французский, испанский, итальянский и другие языки.

Кодирование информации

С появлением языка, а затем и знаковых систем расширились возможности общения между людьми. Это позволило хранить идеи, полученные знания и любые данные, передавать их различными способами на расстояние и в другие времена — не только своим современникам, но и будущим поколениям. До наших дней дошли творения предков, которые с помощью различных символов увековечили себя и свои деяния в памятниках и надписях. Наскальные рисунки(петроглифы) до сих пор служат загадкой для ученых. Возможно, таким способом древние люди хотели вступить в контакт с нами, будущими жителями планеты и сообщить о событиях их жизни.

Каждый народ имеет свой язык, состоящий из набора символов (букв): русский, английский, японский и многие другие. Вы уже познакомились с языком математики, физики, химии.

Представление информации с помощью какого-либо языка часто называют кодированием.

Код — набор символов (условных обозначений) дли представления информации. Кодирование — процесс представления информации в виде кода.

Водитель передает сигнал с помощью гудка или миганием фар. Кодом является наличие или отсутствие гудка, а в случае световой сигнализации — мигание фар или его отсутствие.

Вы встречаетесь с кодированием информации при переходе дороги по сигналам светофора. Код определяют цвета светофора — красный, желтый, зеленый.

В основу естественного языка, на котором общаются люди, тоже положен код. Только в этом случае он называется алфавитом. При разговоре этот код передается звуками, при письме — буквами. Одну и ту же информацию можно представить с помощью различных кодов. Например, запись разговора можно зафиксировать посредством русских букв или специальных стенографических значков. По мере развития техники появлялись разные способы кодирования информации. Во второй половине XIX века американский изобретатель Сэмюэль Морзе изобрел удивительный код, который служит человечеству до сих пор. Информация кодируется тремя «буквами»: длинный сигнал (тире), короткий сигнал (точка) и отсутствие сигнала (пауза) для разделения букв. Таким образом, кодирование сводится к использованию набора символов, расположенных в строго определенном порядке.

Люди всегда искали способы быстрого обмена сообщениями. Для этого посылали гонцов, использовали почтовых голубей. У народов существовали различные способы оповещения о надвигающейся опасности: барабанный бой, дым костров, флаги и т. д. Однако использование такого представления информации требует предварительной договоренности о понимании принимаемого сообщения.

Знаменитый немецкий ученый Готфрид Вильгельм Лейбниц предложил еще в XVII веке уникальную и простую систему представления чисел. «Вычисление с помощью двоек. является для науки основным и порождает новые открытия. при сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок».

Сегодня такой способ представления информации с помощью языка, содержащего всего два символа алфавита — 0 и 1, широко используется в технических устройствах, в том числе и в компьютере. Эти два символа 0 и 1 принято называть двоичными цифрами или битами (от англ. bit — Binary Digit — двоичный знак). Инженеров такой способ кодирования привлек простотой технической реализации — есть сигнал или нет сигнала. С помощью этих двух цифр можно закодировать любое сообщение.

Более крупной единицей измерения объема информации принято считать 1 байт, который состоит из 8 бит.

Принято также использовать и более крупные единицы измерения объема информации. Число 1024 (2 10 ) является множителем при переходе к более высокой единице измерения.