Фазовый переход
Компания OCZ, более известная, как производитель очень хороших оверклокерских модулей памяти, а с недавнего времени, и блоков питания повышенной мощности, объявила свою первую систему охлаждения, типа «фреонка», или «система фазового перехода», по-научном
Компания OCZ, более известная, как производитель очень хороших оверклокерских модулей памяти, а с недавнего времени, и блоков питания повышенной мощности, объявила свою первую систему охлаждения, типа «фреонка», или «система фазового перехода», по-научному. Интерес система представляет своей маленькой ценой — $299. Аналогичные системы фазового перехода от других компаний, типа Asetek, стоят дороже почти в два раза, однако, и обеспечивают лучшую производительность.
Система фазового перехода сможет охладить ваш процессор, или видеокарту до градусов ниже нуля, что положительно скажется на потенциале для разгона и установки новых рекордов. Это для тех, кто не знал :).
Термодинамическая фаза. Фазовый переход
Термодинамическая фаза – термодинамически однородная по свойствам часть термодинамической системы, отделенная от других фаз поверхностями раздела, на которых скачком изменяются некоторые свойства системы1.
В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру.
Газ всегда состоит из одной фазы, жидкость может состоять из нескольких жидких фаз разного состава, но двух разных жидкостей одного состава в равновесии сосуществовать не может. Вещество в твердом состоянии может состоять из нескольких фаз, причем некоторые из них могут иметь одинаковый состав, но различную структуру (полиморфные модификации, аллотропия).
Агрегатное состояние — состояние вещества, характеризующееся определёнными качественными свойствами — способностью или неспособностью сохранять объём и форму, наличием или отсутствием дальнего и ближнего порядка и другими.
Изменение агрегатного состояния сопровождается скачкообразным изменением свободной энергии, энтропии, плотности и других основных физических свойств. Выделяют следующие агрегатные состояния: твёрдое тело, жидкость, газ, плазма.
Набор термодинамических фаз вещества обычно значительно богаче набора агрегатных состояний, то есть одно и то же агрегатное состояние вещества может находиться в различных термодинамических фазах (лед, например, встречается в пяти различных модификациях — фазах). Именно поэтому описание вещества в терминах агрегатных состояний довольно огрублённое, и оно не может различить некоторые физические разные ситуации.
В любом случае при наличии раздела фаз подразумевается принципиальная возможность перехода вещества из одной фазы в другую.
Фазовый переход (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий.
Значение температуры, давления или какой-либо другой физической величины, при котором происходят фазовые переходы в однокомпонентной системе, называют точкой перехода.
Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую).
Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.
Различают фазовые переходы двух родов.
Фазовый переход первого рода (например, плавление, кристаллизация и т.д.) сопровождается поглощением или выделением теплоты, называемой теплотой фазового перехода.
При фазовом переходе первого рода скачкообразно изменяются самые главные, первичные экстенсивные параметры: удельный объём, количество запасённой внутренней энергии, концентрация компонентов и т. п.
Наиболее распространённые примеры фазовых переходов первого рода: плавление и кристаллизация, испарение и конденсация, сублимация и десублимация.
Фазовые переходы первого рода характеризуются постоянством температуры, изменениями энтропии и объёма. Объяснение этому можно дать следующим образом.
Под скачкообразным изменением свойств вещества имеется в виду скачок при изменении температуры и давления. В реальности же, воздействуя на систему, мы изменяем не эти величины, а её объем и её полную внутреннюю энергию. Это изменение всегда происходит с какой-то конечной скоростью, а значит, что для того, чтобы «покрыть» весь разрыв в плотности или удельной внутренней энергии, нам требуется некоторое конечное время. В течение этого времени фазовый переход происходит не сразу во всём объёме вещества, а постепенно. При этом в случае фазового перехода первого рода выделяется (или забирается) определённое количество энергии, которая называется скрытой теплотой фазового перехода. Для того, чтобы фазовый переход не останавливался, требуется непрерывно отводить (или подводить) это тепло, либо компенсировать его совершением работы над системой.

Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решётки. Подводимая при плавлении теплота идёт не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. При подобных переходах – из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние – степень беспорядка увеличивается и, с точки зрения второго начала термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.
Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объема, называются фазовыми переходами второго рода.
Эти переходы характеризуются постоянством объема и энтропии. При этом плотность и внутренняя энергия так же не меняются, так что невооружённым глазом такой фазовый переход может быть незаметен. Скачок же испытывают их производные по температуре и давлению: теплоёмкость, коэффициент теплового расширения, различные восприимчивости и т. д.
Общая трактовка фазовых переходов II рода предложена советским ученым Л. Д. Ландау (1908—1968). Согласно этой трактовке, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода.
Наиболее распространённые примеры фазовых переходов второго рода: прохождение системы через критическую точку, переход парамагнетик-ферромагнетик или парамагнетик — антиферромагнетик, переход металлов и сплавов в состояние сверхпроводимости, переход жидкого гелия в сверхтекучее состояние, переход аморфных материалов в стеклообразное состояние.
Современная физика исследует также системы, обладающие фазовыми переходами третьего или более высокого рода. В последнее время широкое распространение получило понятие квантовый фазовый переход, т.е. фазовый переход, управляемый не классическими тепловыми флуктуациями, а квантовыми, которые существуют даже при абсолютном нуле температур.
Деление фазовых переходов на два рода несколько условно, так как бывают фазовые переходы первого рода с малыми скачками параметра порядка и малыми теплотами перехода при сильно развитых флуктуациях. Это наиболее характерно для переходов между жидкокристаллическими фазами.
Квантовый компьютер смоделировал квантовый фазовый переход

Группа Михаила Лукина впервые экспериментально исследовала квантовый фазовый переход в сильно скоррелированной системе. Для этого ученые использовали 51-кубитный квантовый компьютер, разработанный ими в 2017 году. Физикам не просто удалось проверить закон универсальности фазовых переходов и подтвердить простую модель Киббла-Журека, но и воспроизвести современные теоретические поправки. Статья опубликована в Nature, препринт работы выложен на arXiv.org.
Как правило, в повседневной жизни мы наблюдаем фазовые переходы первого рода — превращения вещества, в ходе которых скачкообразно изменяется его внутренняя энергия, концентрация или удельный объем. Простейшие примеры таких переходов — это плавление льда и испарение воды. В то же время, в природе также встречаются фазовые переходы второго рода, в которых скачкообразно меняются первые производные перечисленных выше параметров. Заметить такие переходы невооруженным глазом практически невозможно, однако они играют важную роль в современной науке и технике. Например, превращение металлов в сверхпроводники или переход жидкого гелия в сверхтекучее состояние относят именно к переходам второго рода.
Первая теория переходов второго рода была построена Львом Ландау еще в 30-х годах прошлого века. Согласно этой теории, такие переходы всегда связаны с изменением симметрии вещества. Например, при фазовом переходе парамагнетик — ферромагнетик в веществе появляется выделенная ось, направление которой совпадает со спонтанной намагниченностью. Следовательно, после перехода система будет инвариантна только относительно вращений вокруг оси намагниченности, тогда как в исходной системе таких ограничений не было. К сожалению, теория Ландау носит скорее качественный характер и предсказывает далеко не все наблюдаемые эффекты. Более корректно неравновесную динамику фазового перехода второго рода описывает механизм Киббла—Журека (Kibble—Żurek mechanism), предложенный около сорока лет назад. Эта теория учитывает, что около точки перехода динамика системы замедляется, а потому на первый план выходят тепловые флуктуации, которые определяют формирование топологических дефектов. К настоящему времени экспериментаторы успели проверить этот механизм для большого числа физических систем.
Кроме того, недавно механизм Киббла—Журека распространили на квантовые системы, в которых динамика фазового перехода определяется не тепловыми, а квантовыми флуктуациями. Оказалось, что в этом случае к стандартной критической экспоненте, связанной с корреляционной длиной, добавляется динамическая критическая экспонента, которая описывает масштаб пространства-времени около критической точки. Более того, итоговое значение критической экспоненты, которое складывается из этих двух эффектов и описывает скорость роста скоррелированных регионов (примесей новой фазы), определяется только классом универсальности квантового фазового перехода. Этот механизм имеет много практических применений — например, с его помощью можно описывать динамику квантового компьютера. К сожалению, предсказания этой теории для сильно скоррелированных систем, к которым относятся квантовые компьютеры, до сих пор физикам удавалось проверить только в общих чертах.
Группа физиков под руководством Михаила Лукина одной из первых исследовала квантовый фазовый переход в режиме реального времени. Для этого ученые использовали квантовый 51-кубитный квантовый компьютер, который работает с ульрахолодными атомами рубидия-87, пойманными в оптическую ловушку и выстроенными в одномерную цепочку. «Нулем» каждого кубита такого компьютера служит основное состояние атома, «единицей» — сильно возбужденное ридберговское состояние. Изменяя интенсивность удерживающих лазеров, физики могут контролировать силу взаимодействия соседних атомов и моделировать системы с разной симметрией. Поэтому в каком-то смысле компьютер можно считать полностью программируемым. Подробнее об устройстве этого компьютера можно прочитать в материале «Пятьдесят кубитов и еще один».
С помощью квантового компьютера ученые смоделировали несколько квантовых систем, обладающих разными симметриями. Для этого ученые изменяли частоту «расстройки» Δ (detuning frequency) и частоту Раби Ω, которые определяют когерентную связь между соседними атомами. При отрицательных значениях частоты Δ наименьшей энергией обладает «неупорядоченная» фаза, в которой все атомы цепочки находятся в основном состоянии. Симметрия такой фазы максимальна. Однако при положительных значениях Δ более предпочтительной становится «упорядоченная» фаза, в которой часть атомов возбуждаются. В зависимости от соотношения между частотами Δ и Ω, возбужденные атомы могут перемежаться одним, двумя, тремя или большим количеством атомов в основном состоянии. Фазу, в которой один период содержит N атомов, физики назвали ℤN-упорядоченной. Например, состояние системы, в которой возбужденные атомы следуют через одного, отвечает ℤ2-упорядоченной фазе. Очевидно, чем больше значение N, тем ниже симметрия ℤN-упорядоченной фазы.
Чтобы исследовать переход между «неупорядоченной» и ℤN-упорядоченной фазой, физики действовали по следующей схеме. Сначала они держали частоту Δ отрицательной и медленно включали частоту Ω, чтобы перевести систему в «неупорядоченную» фазу. Затем исследователи повышали частоту Δ с постоянной скоростью (не обязательно медленно) до некоторого фиксированного значения, определяющего тип «упорядоченной» фазы. После этого ученые медленно выключали частоту Ω и измеряли квантовые состояния атомов. Наконец, используя эти состояния, физики находили корреляционную функцию Ридберга и извлекали из нее корреляционную длину.

(a) Численно рассчитанная фазовая картина трех рассмотренных переходов. Цветные области приведены для удобства. (b) Типичное поведение корреляционных функций для соответствующих фазовых переходов
Переносим тепло
А что такое на самом деле теплота? Когда прикасаемся к теплому предмету, наши нервы ощущают приток тепла от него. А когда прикасаемся к холодному предмету, наоборот, наши нервы ощущают обратный отток тепла от нас к более холодному предмету. Мы способны замечать температуру предметов на ощупь (теплые или холодные), потому что наши нервные окончания фиксируют тепловые потоки, которые переходят от этих предметов к нам или обратно, от нас к ним.
Так что же такое теплота на языке физики? Теплота — это энергия, которая переходит от физических тел, имеющих более высокую температуру, к физическим телам с более низкой температурой. В системе СИ единицей измерения этой энергии является джоуль (Дж).
Укутаемся в одеяло
Почему одеяло согревает нас? Разве мы не отдаем тепло через одеяло окружающей среде? Нет, определенно отдаем, но когда масса одеяла и изолированный в нем воздух достаточно нагреются, то скорость передачи тепла от тела к одеялу заметно снижается. Дело в том, что толстое одеяло медленно передает полученное тепло окружающему воздуху. Чем одеяло толще, тем медленнее тепло от тела передается более холодной окружающей среде.
Откуда берется тепловая энергия? Если посмотреть с молекулярной точки зрения, то теплота— это мера энергии движения молекул внутри физического тела. Тепловая энергия содержится в теле, если только не выйдет из него в окружающую среду.
Разные материалы могут хранить разное количество теплоты. Нагретый картофель хранит тепло дольше (это может подтвердить ваш язык), чем менее плотные материалы, как сладкая вата. Мера количества теплоты, содержащейся в теле, называется удельной теплоемкостью.
Физикам нравится все измерять, и не удивительно, что наблюдая, как кто-то варит себе чашку кофе, после прочтения этих строк вам захочется схватить термометр и измерить температуру напитка. Допустим, что в емкости находится ровно 1 кг варящегося кофе. Для увеличения температуры кофе на 1°С потребуется 4186 Дж тепловой энергии, но для увеличения температуры стекла массой 1 кг на тот же 1°С нужно всего лишь 840 Дж. Куда же уходит эта энергия? Она уходит в нагреваемое тело, которое хранит ее в качестве внутренней энергии, пока полученная энергия снова не окажется за пределами тела.
Если для увеличения температуры 1,0 кг кофе на 1°С требуется 4186 Дж, то для увеличения температуры на 1°С кофе массой 2 кг потребуется в два раза больше энергии, т.е. 8372 Дж.
Количество теплоты, ( Q ) (наиболее распространенное обозначение теплоты; впрочем, это не имеет значения), которое требуется для увеличения температуры тела, можно связать с изменением этой температуры и имеющейся массой тела:
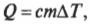
где ( Q ) — это количество тепловой энергии (измеряемой в джоулях, если используется система СИ), ( m ) — величина массы, ( Delta T ) — изменение температуры, а ( c ) — удельная теплоемкость, измеряемая в системе СИ в Дж/(кг·°С).
Одна калория определяется как количество теплоты, нужное для нагревания 1 г воды на 1°С, таким образом 1 калория = 4,186 Дж. Диетологи используют эту единицу измерения для обозначения условной энергетической ценности продуктов питания. Например, на упаковках продуктов питания можно найти обозначение “ккал” (килокалория), причем 1 ккал = 1000 калорий, т.е. 1 ккал = 4186 Дж. Кроме того, физики используют еще один термин — британскую тепловую единицу (British thermal unit — BTU). BTU равна количеству теплоты, требуемому для нагревания 1 фунта (около 454 г) воды на 1°F. Для преобразования BTU в джоули можно пользоваться равенством 1 BTU = 1055 Дж.
Представьте себе, что, находясь в гостях, вы обнаружили, что кофе в вашей чашке (около 45 г) остыл. “Здесь 45°С, а мне нравится, чтобы было 65°С”, — говорите вы. Хозяин в ответ предлагает долить вам более горячего кофе.
“Минуточку, — говорите вы. — Температура кофе в кофейнике равна 95°С. Подождите, я подсчитаю, сколько надо долить.”
Вот тепловая энергия, теряемая массой ( m_1 ) нового более горячего кофе:
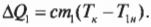
А вот тепловая энергия, получаемая массой ( m_2 ) более холодного кофе, уже имевшегося в чашке:
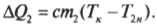
Предположим, что во время этой операции кофейная чашка является суперизолятором, который не рассеивает свою тепловую энергию в окружающую среду. Тогда тепловая энергия, теряемая новым более горячим кофе, равна теплоте, получаемой уже имевшимся в чашке более холодным кофе, то есть:
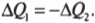
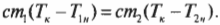
Поделив обе части равенства на удельную теплоемкость и подставив числа, получаем:
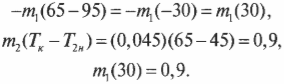
Поделив обе части последнего равенства на 30, получаем:
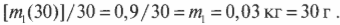
Теперь можно отложить свой калькулятор в сторону и попросить: “Налейте мне ровно 30 г горячего кофе из кофейника, пожалуйста”.
Умения
Умение использовать классические методы для описания фазовых переходов первого и второго рода.
Навык применять базовые знания в области математики, физики и других наук в профессиональной деятельности, в том числе для проведения научных исследований, анализа объектов, систем, процессов, явлений и методов, их экспериментального и теоретического включая построение их качественных и количественных моделей изучения и для использования полученных результатов на практике.
понадобится для освоения
для зачета в своем вузе

Васильев Олег Станиславович
Кандидат физико-математических наук
Должность: Доцент отделения лазерных и плазменных технологий офиса образовательных программ НИЯУ МИФИ