


• Испытание — комплекс условий появления какого-либо случайного явления.
• Событие — исход испытания.
• Частота события — отношение числа наступлений события к числу испытаний.
• Вероятность события — мера объективной возможности появления события.
• Достоверное — событие, которое обязательно наступает при испытании.
• Невозможное — событие, которое не может наступить при испытании.
• Несовместные события — наступление одного исключает наступление других.
• Независимые события — вероятности наступления событий не зависят от наступления других событий.
• Полная система событий — совокупность несовместимых событий, хотя бы одно из которых обязательно наступит при испытании.
• Если при испытании может наступить только два события и одно из них исключает наступление другого, то они называются противоположными.
Классическое определение вероятности события: 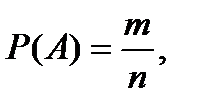
где А — событие, Р(А) — вероятность события, n — число всех исходов (несовместных, единственно возможных и равновозможных), m – число исходов, связанных с наступлением данного события А.
Пример 1.1.Брошены две игральные кости. Найти вероятность того, что сумма очков, выпавших на верхних гранях равна 6.
Решение.А – событие, состоящее в том, что сумма выпавших на двух игральных костях очков равна 6. Согласно классическому определению вероятности события: 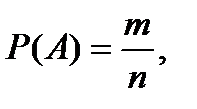 где n=62=36 – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=5 (1+5=5+1=2+4=4+2=3+3=6) – все возможные варианты получения в сумме 6 очков при подбрасывании двух игральных костей.
где n=62=36 – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=5 (1+5=5+1=2+4=4+2=3+3=6) – все возможные варианты получения в сумме 6 очков при подбрасывании двух игральных костей. 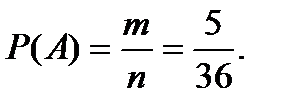
Пример 1.2. В городе имеется одиннадцать различных коммерческих банков. Господин «N» открыл по одному счету в пяти различных банках. Позднее четыре банка из одиннадцати изменили ставки процентов по вкладам. Найти вероятность того, что по двум вкладам господина ставки остались неизменными.
Решение. Господин выбирал банки случайным образом. Испытание -выбор пяти банков из имеющихся одиннадцати. А – событие, состоящее в том, что по двум вкладам господина, из имеющихся пяти, ставки остались неизменными, и, следовательно, по трем другим изменились.
Р(А)= 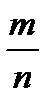 , где n=
, где n= 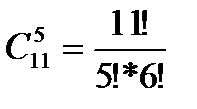 =462 — число всех исходов испытания (несовместных, единственно возможных и равновозможных); m =
=462 — число всех исходов испытания (несовместных, единственно возможных и равновозможных); m = 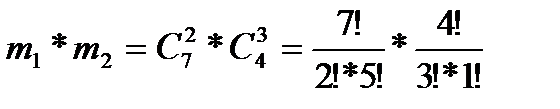 =21*4=84- число исходов, связанных с наступлением события А (m1— число вариантов выбора двух банков, изимеющихся семи, не изменивших ставки процентов, m2— число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).
=21*4=84- число исходов, связанных с наступлением события А (m1— число вариантов выбора двух банков, изимеющихся семи, не изменивших ставки процентов, m2— число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов). 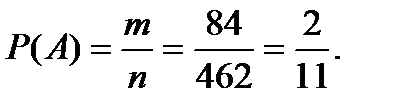
Пример 1.3. Номер телефона включает шесть цифр (от ноля до девяти). Найти вероятность того, что случайно набранный номер окажется верным.
Решение. Испытание — набор любых шести цифр, причем каждая из них может быть любой из десяти — от ноля до девяти. А— событие состоящее в том, что случайно набранный номер верен. Р(А)= 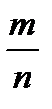 , где n=106- число всех исходов испытания (несовместимых, единственно возможных и равновозможных); m=1 – число исходов, связанных с наступлением события А.
, где n=106- число всех исходов испытания (несовместимых, единственно возможных и равновозможных); m=1 – число исходов, связанных с наступлением события А. 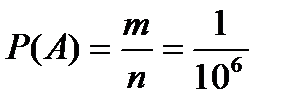 .
.
Пример 1.4.Из букв разрезной азбуки составлено слово «ананас». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось исходное слово.
Решение. А – событие, состоящее в том, что случайно собрано слово «ананас». 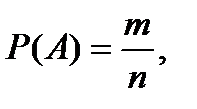 где n=6! – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=3!2! – число благоприятных исходов, так как повторяющиеся буквы «а» и «н» можно произвольным образом переставлять между собой.
где n=6! – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=3!2! – число благоприятных исходов, так как повторяющиеся буквы «а» и «н» можно произвольным образом переставлять между собой. 
311 вариант Ларина
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
1
Затраты на покупку огурцов возросли на 92%, а цена килограмма огурцов увеличилась на 60%. На сколько процентов увеличился вес купленных огурцов?
2
На тренировке в 50‐метровом бассейне пловец проплыл 200‐метровую дистанцию. На рисунке изображен график зависимости расстояния s (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца. Определите по графику, какое расстояние преодолел пловец за 2 мин 20 с.
3
Найдите косинус угла АВС, изображенного на рисунке
4
Из шести букв разрезной азбуки составлено слово «АНАНАС». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «АНАНАС». Ответ округлите до тысячных.
5
Найдите (x_0) ‐ наибольший отрицательный корень уравнения [sqrt<-3sin x+cos x>=sqrt
6
Две окружности с центрами в точках (O) и (O_1) и радиусами 5 и 3 соответственно касаются сторон угла (A) ((B) и (B_1) – точки касания). Найдите расстояние между центрами окружностей, если (AB_1=4.) Ответ округлите до десятых.
7
Точка движется по координатной прямой согласно закону (x(t)=3+2t+t^2,) где (x(t)) ‐ координата точки в момент времени (t.) В какой момент времени скорость
точки будет равна 5?
8
Четырехугольная пирамида весом 27 кг горизонтальными плоскостями разрезана на 3 части одинаковой высоты. Найдите вес в килограммах нижней части пирамиды.
9
Найдите значение выражения:
10
Водолазный колокол, содержащий (v=3) моль воздуха при давлении (p_1=1,8) атмосферы, медленно опускают на дно водоема. При этом происходит сжатие воздуха до конечного давления (p_2.) Работа, совершаемая водой при сжатии воздуха, определяется выражением (A=alpha v Tlog_2 frac
11
Поезд отправился со станции А, проследовал через станции В и С, прибыл на станцию D. Пусть ВС больше АВ на (frac<1><4>) часть АВ, а CD на 60% меньше ВС. Найдите среднюю скорость поезда на пути AD, если его скорость на АВ, ВС и CD равнялась соответственно 80 км/ч, 100 км/ч, 180 км/ч. Ответ дайте в км/ч.
12
Найдите точку минимума функции (y=ln (2x+5)+frac<2><(2x+5)^2>)
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Часть 2
13
а) Решите уравнение ((cos 2x+3sin x-2)cdotsqrt
б) Укажите корни этого уравнения, принадлежащие отрезку ([0;pi])
14
В правильной четырехугольной пирамиде плоскость (alpha,) проведенная через сторону основания, делит двухгранный угол при основании пирамиды и боковую поверхность пирамиды пополам.
а) Докажите, что двухгранный угол при основании пирамиды равен (45^circ.)
б) Найдите расстояние от плоскости (alpha) до вершины пирамиды, если сторона основания пирамиды равна 1.
15
16
(Д.Сверак sverak_fm) В трапеции ABCD (AD – нижнее основание) площади треугольников ABD и BDC равны соответственно 12 и 4, а точка G является серединой BD. Ниже прямой AD выбрана точка Е, АЕ=BD, а на отрезке ЕС выбрана точка F такая, что CF в 4 раза короче СЕ.
А) Докажите, что (angle BFG=90^circ)
Б) Найдите длину отрезка BD, если дополнительно известно, что (angle CFG =75^circ, angle DGC=15^circ)
17
В июле планируется взять кредит в банке на сумму 1,6 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
‐ каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года;
‐ с февраля по июнь каждого года необходимо выплатить часть долга
‐ в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж в 2 раза больше наименьшего?
(Задача предложена М.Резник)
18
Найдите все значения параметра (a,) при каждом из которых наименьшее значение функции (f(x)=-x^4+frac<2ax^3><9>+frac
Имеются два многочлена от целочисленной переменной (x):
[q(x)=1+x+x^2+…+x^k] Рассмотрим функцию (f(x)=frac
а) Может ли функция (f(x)) (принимать не целые значения при (k =3?)
б) Может ли функция (f(x)) принимать не целые значения при (k =2?)
в) При каких натуральных значениях (k) функция (f(x)) может принимать только целые значения?
Из букв разрезной азбуки составлено слово статистика
• Испытание – комплекс условий появления какого-либо случайного явления.
• Событие – исход испытания.
• Частота события – отношение числа наступлений события к числу испытаний.
• Вероятность события – мера объективной возможности появления события.
• Достоверное – событие, которое обязательно наступает при испытании.
• Невозможное – событие, которое не может наступить при испытании.
• Несовместные события – наступление одного исключает наступление других.
• Независимые события – вероятности наступления событий не зависят от наступления других событий.
• Полная система событий – совокупность несовместимых событий, хотя бы одно из которых обязательно наступит при испытании.
• Если при испытании может наступить только два события и одно из них исключает наступление другого, то они называются противоположными.
Классическое определение вероятности события: 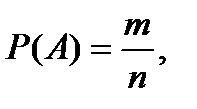
где А – событие, Р(А) – вероятность события, n – число всех исходов (несовместных, единственно возможных и равновозможных), m – число исходов, связанных с наступлением данного события А.
Пример 1.1.Брошены две игральные кости. Найти вероятность того, что сумма очков, выпавших на верхних гранях равна 6.
Решение.А – событие, состоящее в том, что сумма выпавших на двух игральных костях очков равна 6. Согласно классическому определению вероятности события: 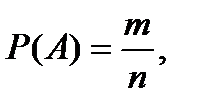 где n=62=36 – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=5 (1+5=5+1=2+4=4+2=3+3=6) – все возможные варианты получения в сумме 6 очков при подбрасывании двух игральных костей.
где n=62=36 – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=5 (1+5=5+1=2+4=4+2=3+3=6) – все возможные варианты получения в сумме 6 очков при подбрасывании двух игральных костей. 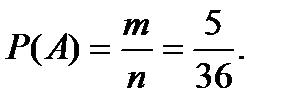
Пример 1.2. В городе имеется одиннадцать различных коммерческих банков. Господин «N» открыл по одному счету в пяти различных банках. Позднее четыре банка из одиннадцати изменили ставки процентов по вкладам. Найти вероятность того, что по двум вкладам господина ставки остались неизменными.
Решение. Господин выбирал банки случайным образом. Испытание -выбор пяти банков из имеющихся одиннадцати. А – событие, состоящее в том, что по двум вкладам господина, из имеющихся пяти, ставки остались неизменными, и, следовательно, по трем другим изменились.
Р(А)= 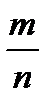 , где n=
, где n= 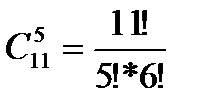 =462 – число всех исходов испытания (несовместных, единственно возможных и равновозможных); m =
=462 – число всех исходов испытания (несовместных, единственно возможных и равновозможных); m = 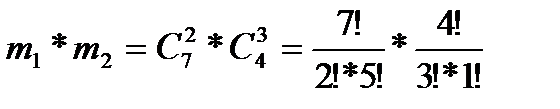 =21*4=84- число исходов, связанных с наступлением события А (m1– число вариантов выбора двух банков, изимеющихся семи, не изменивших ставки процентов, m2– число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов).
=21*4=84- число исходов, связанных с наступлением события А (m1– число вариантов выбора двух банков, изимеющихся семи, не изменивших ставки процентов, m2– число вариантов выбора трех банков, из имеющихся четырех, изменивших ставки процентов). 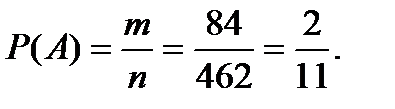
Пример 1.3. Номер телефона включает шесть цифр (от ноля до девяти). Найти вероятность того, что случайно набранный номер окажется верным.
Решение. Испытание – набор любых шести цифр, причем каждая из них может быть любой из десяти – от ноля до девяти. А– событие состоящее в том, что случайно набранный номер верен. Р(А)= 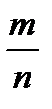 , где n=106- число всех исходов испытания (несовместимых, единственно возможных и равновозможных); m=1 – число исходов, связанных с наступлением события А.
, где n=106- число всех исходов испытания (несовместимых, единственно возможных и равновозможных); m=1 – число исходов, связанных с наступлением события А. 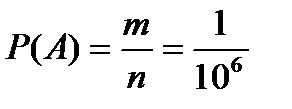 .
.
Пример 1.4.Из букв разрезной азбуки составлено слово «ананас». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось исходное слово.
Решение. А – событие, состоящее в том, что случайно собрано слово «ананас». 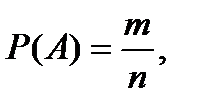 где n=6! – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=3!2! – число благоприятных исходов, так как повторяющиеся буквы «а» и «н» можно произвольным образом переставлять между собой.
где n=6! – число всех возможных исходов (несовместных, единственно возможных и равновозможных); m=3!2! – число благоприятных исходов, так как повторяющиеся буквы «а» и «н» можно произвольным образом переставлять между собой. 
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10077 –  | 7520 –
| 7520 –  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Ответ или решение 1
![]()
Нам нужно посчитать вероятность взаимосвязанных событий.
Рассчитаем вероятности появления нужных букв (каждая следующая буква появляется при условии, что предыдущее событие произошло):
Найдем вероятность выбора первой буквы Р:
Количество событий = общему количеству букв = 6.
Из них благоприятных событий (подходящих букв) = 1.
Вероятность по формуле Лапласа:
Вероятность, что вторая буква Е:
Р = 1/5 (из оставшихся 5ти букв 1 Е);
Вероятность того, что третья буква будет К:
Р = 1/4 (из оставшихся 4х букв 1 К);
Вероятность того, что четвертая буква будет А:
Р = 2/3 (из оставшихся 3х букв 2 А);
Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А:
Р = (1 / 6) * (1 / 5) * (1 / 4) * (2 / 3) = 1/180.
Слово «тройка» составлено из букв разрезной азбуки. Карточки с буквами перемешиваются и из них по очереди извлекаются 4 карточки. Какова вероятность того, что эти 4 карточки составят слово «крот» ? Рассмотреть два случая: 1) карточки располагаются в порядке извлечения; 2) вынутые карточки можно переставлять.
задан 20 Сен ’16 20:30
Буквы слова здесь не повторяются. Четыре буквы из шести извлекаются $%C_6^4=C_6^2=15$% равновероятными способами. Поэтому с вероятностью 1/15 извлечённые буквы могут составить слово «крот» после перестановки.Это пункт 2.
В пункте 1 можно просто перемножить вероятности. Нужные нам буквы извлекаются из имеющегося количества с вероятностями 1/6, 1/5, 1,4, 1/3 соответственно. Вероятность равна 1/N, где N=6x5x4x3=360.
Здравствуйте
Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Задачи с элементами комбинаторики. Задача о выборке
Задача о выборке. Среди N элементов некоторой совокупности содержится M элементов, обладающих определенным свойством. Случайным образом отбираются n элементов. Найти вероятность того, что среди них окажется m элементов, обладающих указанным свойством.
Решение. В данном случае порядок следования элементов не имеет значения, поэтому множество элементарных исходов состоит из всех сочетаний 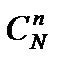 , составленных из N элементов по n. Благоприятными будут те исходы, когда в выборку попадут m элементов из М, обладающих определенным свойством. Такой выбор можно осуществить
, составленных из N элементов по n. Благоприятными будут те исходы, когда в выборку попадут m элементов из М, обладающих определенным свойством. Такой выбор можно осуществить 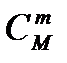 способами. Но при этом вместе с указанными т элементами в выборку должны попасть п – т элементов из числа N – M элементов данной совокупности, не обладающих этим свойством. А этот отбор можно осуществить
способами. Но при этом вместе с указанными т элементами в выборку должны попасть п – т элементов из числа N – M элементов данной совокупности, не обладающих этим свойством. А этот отбор можно осуществить 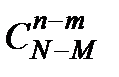 способами. Таким образом, число всех благоприятстующих исходов испытания равно
способами. Таким образом, число всех благоприятстующих исходов испытания равно 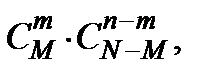 а искомая вероятность принимает вид
а искомая вероятность принимает вид
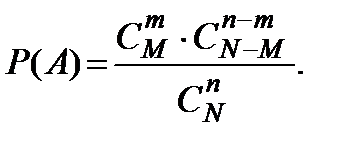
Пример 1. Первые 7 букв русского алфавита написаны на карточках. Случайным образом последовательно извлекаются четыре карточки. Найти вероятность того, что полученное “слово” будет оканчиваться буквой а.
Решение. Любой набор из четырех букв здесь считается словом, поэтому порядок следования букв имеет значение. Число 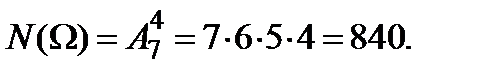 Так как последняя буква слова известна, то количество слов с буквой а в конце равно числу размещений из 7 элементов по 3:
Так как последняя буква слова известна, то количество слов с буквой а в конце равно числу размещений из 7 элементов по 3:
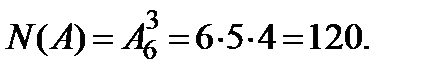
Отсюда искомая вероятность 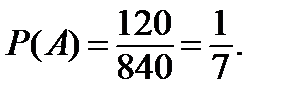
Пример 2. На шести карточках написаны буквы А, В, К, М, О, С. После перетасовки случайным образом выбирают одну карточку за другой и раскладывают их в том порядке, в котором они были вынуты. Найти вероятность того, что на карточках будет написано слово МОСКВА.
Решение. Множество элементарных исходов состоит из всех перестановок из шести разных элементов, 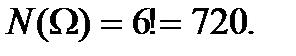 Интересующему нас событию соответствует лишь один исход. Поэтому
Интересующему нас событию соответствует лишь один исход. Поэтому 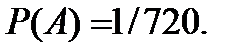
Пример 3. Из разрезной азбуки выкладывается слово МАТЕМАТИКА. Затем все буквы тщательно перемешиваются и снова выкладываются в случайном порядке. Какова вероятность того, что снова получится слово МАТЕМАТИКА?
Решение. В данном случае множество всех букв слова МАТЕМАТИКА состоит из нескольких групп: три буквы А, по две буквы М и Т, по одной букве Е, И и К. Поэтому множество элементарных исходов состоит из всех перестановок с повторениями из 10 элементов, разбитых на указанные группы.
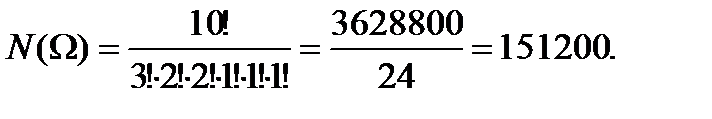
4.1. Слово АЗИМУТ составлено из букв разрезной азбуки. Карточки с буквами перемешивают и из них наугад выбирают 4 карточки. Какова вероятность того, что расположенные по порядку карточки составят слово ЗИМА?
4.2. Из букв разрезной азбуки составлено слово ремонт. Карточки перемешивают и наугад вытаскивают 4 карточки, раскладывают их в порядке извлечения. Какова вероятность того, что получим слово море?
4.3. Из пяти карточек с буквами а, б, в, г, д наугад выбирают две и располагают в порядке извлечения. Какова вероятность того, что получится слово да?
4.4. На каждой из пяти карточек написаны буквы А, Б, И, Р, Ж. Карточки перемешивают, берут по одной и кладут последовательно. Какова вероятность того, что получится слово БИРЖА?
4.5. На пяти карточках написаны буквы И, К, М, Н, С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?
4.6. Из букв слова ротор, составленного с помощью разрезной азбуки, наудачу последовательно извлекают 3 буквы. Какова вероятность того, что получится слово тор?
4.7. На шести карточках написаны буквы слова талант. Карточки перемешиваются. Их наудачу располагают одна за другой. Какова вероятность того, что снова получится слово талант?
4.8. На пяти карточках написаны буквы: на двух карточках л, на остальных трех и. Выкладывают наудачу эти карточки в ряд. Какова вероятность того, что при этом получится слово лилии?
4.9. На пяти карточках написаны буквы л, м, о, о, т. Какова вероятность того, что извлекая карточки по одной наугад, получится слово молот?
4.10. Дано 6 карточек с буквами Н, М, И, Я, Л, О. Какова вероятность того, что: а) получится слово ЛОМ, если наугад одна за другой выбираются 3 карточки; б) получится слово молния?
4.11. Из букв А, С, Н, Н, А, А разрезной азбуки составляется наудачу слово, состоящее из 6 букв. Какова вероятность того, что получится слово АНАНАС?
4.12. На 9 одинаковых карточках написаны буквы Е, Е, Р, Р, С, С, Я, Г, И. Эти карточки выкладывают наудачу в ряд. Какова вероятность того, что при этом получится слово РЕГРЕССИЯ?
4.13. Из букв разрезной азбуки составлено слово песня. Какова вероятность получить снова слово песня после перемешивания карточек?
4.14. На пяти карточках написаны буквы Б, Е, Р, С, Т. Эти карточки наудачу разложены в ряд. Какова вероятность того, что получится слово БРЕСТ?
4.15. Из букв разрезной азбуки составлено слово колокол. Карточки перемешиваются. Какова вероятность получить слово колокол?
4.16. В урне 10 шаров, из которых 6 белых, остальные черные. Наудачу извлекают 4 шара. Какова вероятность того, что среди них окажется 3 белых шара?
4.17. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают 3 изделия для контроля. Какова вероятность того, что в полученной выборке окажется одно бракованное изделие?
4.18. Среди 25 студентов группы, в которой 10 девушек разыгрывается 5 билетов. Какова вероятность того, что среди обладателей билетов окажутся 2 девушки?
4.19. В ящике 4 голубых и 5 красных шара. Из ящика наугад вынимают два шара. Какова вероятность того, что эти шары разного цвета?
4.20. Из десяти билетов выигрышными являются два. Какова вероятность того, что среди взятых наудачу пяти билетов один выигрышный?
4.21. В ящике находятся 15 красных, 9 голубых и 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что вынуты 1 зеленый, 2 голубых и 3 красных шара?
4.22. В ящике 10 шаров, из которых 2 белых, 3 красных и 5 голубых. Наудачу извлечены 3 шара. Какова вероятность того, что все 3 шара разного цвета?
4.23. В партии из 15 изделий имеется две дефектных. Наудачу выбирают 4 изделия для контроля. Какова вероятность того, что в этой выборке окажется хотя бы одно дефектное изделие?
4.24. Партия из 20 выловленных рыб подвергается некоторому контролю. Условием непригодности улова является наличие хотя бы одной бракованной рыбы из четырех проверенных. Какова вероятность того, что улов будет признан непригодным, если он содержит 3 недоброкачественные рыбы?
4.25. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее, чем на 3 из 4 поставленных вопросов. Взглянув на первый вопрос билета, студент обнаружил, что он его знает. Какова вероятность того, что студент сдаст зачет?
4.26. В коробке 5 белых, 4 красных и 3 желтых шара. Наудачу вынимают 3 шара. Какова вероятность того, что среди них 2 белых и 1 желтый шар?
4.27. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Какова вероятность того, что среди трех наугад выбранных вопросов студент знает 2 вопроса?
4.28. Из колоды в 36 карт извлекают 4 карты. Какова вероятность того, что все извлеченные карты пиковой масти?
4.29. В лотерее выигрывают 100 билетов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Какова вероятность того, что выигрыш выпадет хотя бы на 1 билет?
4.30. Наудачу выбирают 5 военнослужащих из группы, состоящей из 4 офицеров и 12 солдат. Какова вероятность того, что в группе будет не более двух офицеров?
ОТВЕТЫ: 4.1. 1/360. 4.2. 1/360. 4.3. 0,0167. 4.4. 1/120. 4.5. 1/120. 4.6. 1/15. 4.7. 1/180. 4.8. 1/10. 4.9. 1/60. 4.10. а) 1/120; б) 1/720. 4.11. 1/60. 4.12. 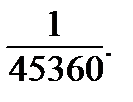 4.13. 1/120. 4.14. 1/120. 4.15. 1/210. 4.16. 8/21. 4.17. 2/40. 4.18. 0,385. 4.19. 5/9. 4.20. 5/9. 4.21. 0,17. 4.22. 0,25. 4.23. 10/21. 4.24. 0,5088. 4.25. 0,901. 4.26. 3/22. 4.27. 0,44.4.28. 0,21·10 -2 . 4.29. 0,69. 4.30. 0,94.
4.13. 1/120. 4.14. 1/120. 4.15. 1/210. 4.16. 8/21. 4.17. 2/40. 4.18. 0,385. 4.19. 5/9. 4.20. 5/9. 4.21. 0,17. 4.22. 0,25. 4.23. 10/21. 4.24. 0,5088. 4.25. 0,901. 4.26. 3/22. 4.27. 0,44.4.28. 0,21·10 -2 . 4.29. 0,69. 4.30. 0,94.
Практическая работа № 1 «Рассмотрение классических примеров теории вероятностей» , страница 2
Решение. Всего кубиков n = 125. Извлечение каждого такого кубика является элементарным исходом в данном опыте. Ожидаемому событию А-извлечению кубика с тремя окрашенными гранями — благоприятствует m = 8 исходов (три окрашенные грани имеет только тот кубик, одна из вершин которого совпадает с вершиной куба).
p(A) = 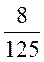 = 0,032.
= 0,032.
Задача 5.
Бросаются два интегральных кубика. Какова вероятность того, что сумма очков окажется равной 7?
Решение. Интегральный кубик может упасть шестью различными способами. Таким образом, общее число возможных элементарных исходов равно 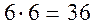 . Подсчитаем число элементарных исходов благоприятствующих событию А (сумма очков равна 7). Семь очков получится, если на первом и втором кубиках будет соответственно: 1 и 6, 2 и 5, 3 и 4, 5 и 2, 6 и 1 очков, т.е. имеется всего 6 исходов, благоприятствующих событию А. Следовательно, искомая вероятность равна
. Подсчитаем число элементарных исходов благоприятствующих событию А (сумма очков равна 7). Семь очков получится, если на первом и втором кубиках будет соответственно: 1 и 6, 2 и 5, 3 и 4, 5 и 2, 6 и 1 очков, т.е. имеется всего 6 исходов, благоприятствующих событию А. Следовательно, искомая вероятность равна
p(A) = 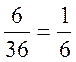 .
.
Задача 6.
Слово “керамит” составлено из букв разрезной азбуки. Затем карточки с буквами перемешиваются и из них извлекаются по очереди четыре карточки. Какова вероятность, что эти четыре карточки составят слово “река”?
Решение. Элементарным исходом является извлечение четырех карточек из семи. По четыре карточки из семи можно извлечь А 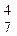 способами. Ожидаемому событию А (выпадение требуемого слова) соответствует только один исход.
способами. Ожидаемому событию А (выпадение требуемого слова) соответствует только один исход.
p(A) = 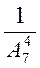 =
= 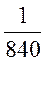 .
.
Задача 7.
В партии из 50 деталей 5 нестандартных. Определить вероятность того, что среди выбранных на удачу для проверки шести деталей две окажутся нестандартными.
Решение. Элементарным исходом является выборка любых шести изделий из пятидесяти. Число n всех таких исходов, очевидно, равно числу сочетаний из пятидесяти по шесть, т.е. С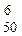 . Нас интересует событие А, состоящее в том, что две из шести деталей нестандартные. Благоприятным исходом для А является любые шесть деталей, из которых две нестандартные и четыре — стандартные. Такого рода групп по шесть деталей имеется С
. Нас интересует событие А, состоящее в том, что две из шести деталей нестандартные. Благоприятным исходом для А является любые шесть деталей, из которых две нестандартные и четыре — стандартные. Такого рода групп по шесть деталей имеется С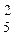 × С
× С 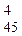 (так как С
(так как С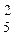 -число всевозможных пар нестандартных деталей, а С
-число всевозможных пар нестандартных деталей, а С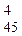 — число всевозможных четверок стандартных деталей и каждая пара нестандартных деталей может оказаться в одной группе с каждой четверкой стандартных деталей).
— число всевозможных четверок стандартных деталей и каждая пара нестандартных деталей может оказаться в одной группе с каждой четверкой стандартных деталей).
p(A) = 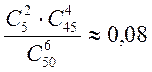 .
.
Задача 8. (пр.20)
r элементарных частиц регистрируются R счетчиками, при чем каждая из частиц может с одинаковой вероятностью попасть в любой из счетчиков. Найти вероятность того, что: а) в определенных R счетчиках окажется по одной частице; б) в каких-то R счетчиках окажется по одной частице.
Решение. Здесь элементарным исходом является размещение r частиц по R счетчикам. Так как каждая частица имеет R различных возможностей (частица может попасть в 1-й счетчик, или во 2-й, или в R-й), то число n всех исходов, т. е. число всех возможных размещений частиц посчетчикам, равно R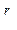 .
.
В случае а) интересующее нас событие А состоит в том, что в определенных R счетчиках окажется по одной частице. Благоприятным исходом для А является размещение частиц по определенным счетчикам в определенном порядке. Таким образом, число m благоприятствующих размещений равно r!
p(A) = 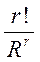 .
.
В случае б) событие А состоит в том, что в любых R счетчиках окажется по одной частице. Благоприятным исходом для А в этом случае является размещение частиц по любой группе из r счетчиков. Так как таких групп будет С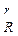 и в каждой группе возможно размещение r частиц r! способами, то число m благоприятствующих размещений равно С
и в каждой группе возможно размещение r частиц r! способами, то число m благоприятствующих размещений равно С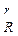 ×
× r!
r!
p(A) = 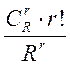 .
.
Задача 9.
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 266
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 171
- БГТУ 602
- БГУ 153
- БГУИР 391
- БелГУТ 4908
- БГЭУ 962
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 119
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 497
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 130
- ИжГТУ 143
- КемГППК 171
- КемГУ 507
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2909
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 107
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 367
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 330
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 636
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 454
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 212
- НУК им. Макарова 542
- НВ 787
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1991
- НГУЭУ 499
- НИИ 201
- ОмГТУ 301
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 119
- РАНХиГС 186
- РОАТ МИИТ 608
- РТА 243
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 122
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 130
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1598
- СПбГТИ (ТУ) 292
- СПбГТУРП 235
- СПбГУ 577
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 193
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 113
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2423
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 324
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 306
Полный список ВУЗов
- О проекте
- Реклама на сайте
- Правообладателям
- Правила
- Обратная связь
Чтобы распечатать файл, скачайте его (в формате Word).















