Сколько битов в байте, Кб, Мб, Гб и Тб

Сколько мегабайт в одном гигабайте или как правильно переводить единицы измерения памяти?

Главная » Компьютерная грамотность » Единицы измерения информации. Что больше кб или Мб? Сколько в 1 Гб Мб?

Если вы очень торопитесь, то посчитайте все нужные вам цифры с помощью онлайн конвертера величин, измеряющих объем информации. Но я рекомендую прочесть статью полностью и поделиться ссылкой в соц. сетях.

В сегодняшней статье мы займемся измерением информации. Все картинки, звуки и видео ролики, которые мы с вами видим на экранах мониторов, представляют собой не более чем цифры. И эти цифры можно измерить, и, сейчас, вы научитесь переводить мегабиты в мегабайты и мегабайты в гигабайты.

Если вам важно знать, сколько в 1 гб мб или сколько в 1 мб кб, то эта статья для вас. Чаще всего такие данные нужны программистам, оценивающим занимаемый их программами объем, но, иногда, не мешает и рядовым пользователям для оценки размера скачиваемых или хранимых данных.

На самом деле, посчитать информацию намного проще, чем изучать высшую математику, достаточно уметь пользоваться калькулятором и знать пару простых правил.

Если вкратце, то достаточно знать это:

1 байт = 8 бит

1 килобайт = 1024 байта

1 мегабайт = 1024 килобайта

1 гигабайт = 1024 мегабайта

1 терабайт = 1024 гигабайта

Общепринятые сокращения: килобайт=кб, мегабайт=мб, гигабайт=гб.

Недавно я получил вопрос от моего читателя: «Что больше кб или мб?». Надеюсь, теперь, ответ на него знает каждый.

Что такое байт. Сколько бит в байте

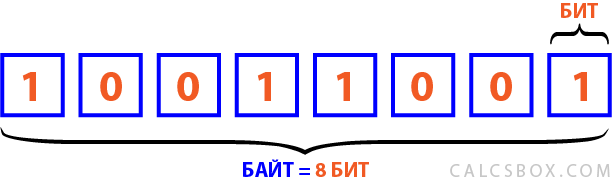
Вы, наверное, слыхали про азбуку Морзе, где комбинации длинных и коротких сигналов (точек и тире) расшифровывались в слова. А если взять комбинацию из 8 цифр, каждая из которых может быть единицей или нулем, то получим 256 комбинаций, чего хватит для отображения и цифр и букв, причем и не одного алфавита. И вот эти 8 бит называются байтом . Таким образом в байте 8 бит.

Бит — это минимальная единица. Она обозначается маленькой буквой «б». Следом за ней идет байт. Он уже обозначается большой буквой «Б».

Почему объем жесткого диска меньше, чем написано на этикетке

Вы возможно уже сталкивались с ситуацией, когда вы купили жесткий диск емкостью 500 ГБ, а операционная система видит заметно меньше, например, только 465 ГБ. Ответ кроется все в тех же приставках и бардаке в их применении. Зато маркетологи знают, как можно буквально по мановению волшебной палочки увеличить емкость дисков своей компании. Достаточно посчитать ее по своей собственной методике.

Производитель может придерживаться при расчетах объема диска международной системы СИ, где гигабайт это 10 9 и напишет на этикетке диска емкостью 500 млрд. байт, что он на 500 ГБ. Когда вы его подключите к компьютеру, то Windows будет считать в двоичной системе и насчитает только 465 ГБ. Причем чем больше емкость диска, тем больше разница между этикеткой и реально доступным объемом. Более того, производитель может посчитать каким-нибудь еще способом, допустим, гигабайт окажется равным 1 млн. килобайт.

Используем конвертер для перевода битов и байтов

Публикация была бы неполной, если бы я не привел инструмент, с помощью которого можно осуществить перевод byte в различные производные. В сети много разнообразных конвертеров, посредством которых можно произвести эти операции. Вот один из них, который мне приглянулся.

Этот конвертер удобен тем, что введя количество byte, можно сразу получить результат во всех возможных измерениях (в том числе перевести биты в байты):

Из данного примера следует, что 3072 байта равно 24576 битам, 3,0720 килобайтам или 3 кибибайтам. Кроме этого, чуть ниже расположены ссылки на миникалькуляторы, где вы сможете быстро произвести конкретный перевод из одной системы единиц в другую.

гигабайт

Гигабайт содержит 1024 мегабайта. Как правило, когда мы префикс Giga, он предлагает миллиард байтов. Это справедливо для десятичной системы счисления, которая основана на коэффициентах 10. Поскольку нам нужно представлять в двоичной системе компьютера, нам нужно использовать двоичный множитель 2 для представления байтов. Это означает, что гигабайт на самом деле содержит 1024 мегабайта. Чтобы оценить, как именно он потребляет память, давайте рассмотрим, что у вас есть 2 ГБ диска. Имея емкость 2 ГБ, вы можете хранить около 500 музыкальных треков.

Терабайт содержит 1024 гигабайта. Приставка Tera предполагает триллион байтов.В двоичной системе это будет 1024 гигабайта. 1 ТБ много места для хранения и, чтобы положить его в перспективе; он может хранить около миллиона фотографий. В настоящее время большинство жестких дисков имеют объем от 1 до 3 ТБ.

Терабайты («ТБ»)

Основываясь на вышеописанной закономерности, верно утверждение, что в одном терабайте («ТБ») находится «1024 гигабайт («ГБ»)». В настоящее время терабайты являются наиболее распространенной единицей измерения объема хранения цифровой информации, особенно, когда речь идет о стандартных размерах жестких дисков («HDD»).

Некоторые примеры возможного массива информации, применительно к значению единицы измерения терабайт, в реальном мире:

«1 ТБ» = Двести тысяч пятиминутных обычных стандартных песен; триста десять тысяч снимков и изображений; или пятьсот часов фильмов.

«10 ТБ» = Количество данных, полученных космическим телескопом «Хаббл» («Hubble Space Telescope») за год.

«24 ТБ» = Количество видеоданных, загруженных на видеохостинг «YouTube» за день в 2016 году.

Представление числовой информации. Сложение и умножение в разных системах счисления

Представление числовой информации с помощью систем счисления

Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.

Система счисления — это система записи чисел с помощью определенного набора цифр.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.

Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.

Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.

Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.

Например: 8527 = 8 ⋅ 10 3 + 5 ⋅ 10 2 + 2 ⋅ 10 1 + 7 ⋅ 10 0 .

Развернутая форма записи чисел произвольной системы счисления имеет вид

$a$ — цифры численной записи, соответствующие разрядам;

$m$ — количество разрядов числа дробной части;

$n$ — количество разрядов числа целой части;

$q$ — основание системы счисления.

Например, запишем развернутую форму десятичного числа $327.46$:

Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.

Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В₁₂ можно расписать так:

7А,5В₁₂ = В ⋅ 12 -2 + 5 ⋅ 2 -1 + А ⋅ 12 0 + 7 ⋅ 12 1 .

В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.

Перевод чисел в позиционных системах счисления

Перевод чисел из произвольной системы счисления в десятичную

Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂ = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 13₁₀;

17D,ECH = 12 ⋅ 16 –2 + 14 ⋅ 16 –1 + 13 ⋅ 160 + 7 ⋅ 16 1 + 1 ⋅ 16 2 = 381,921875.

Перевод чисел из десятичной системы счисления в заданную

Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:

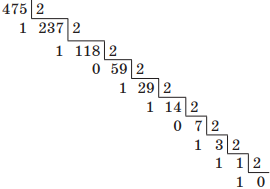
Читая остатки от деления снизу вверх, получим 111011011.

1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 475₁₀.

Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например, переведем десятичную дробь 0,375₁₀ в двоичную систему счисления:

Полученный результат — 0,011₂.

Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2 І ; І = 3).

Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

1234,777₈ = 001 010 011 100,111 111 111₂ = 1 010 011 100,111 111 111₂;

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂.

При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2 І ; І = 4).

Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.

Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.

1234,AB77₁₆ = 0001 0010 0011 0100,1010 1011 0111 0111₂ = 1 0010 0011 0100,1010 1011 0111 0111₂;

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂.

При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.

Например, переведем троичное число 211₃ в семеричную систему счисления. Для этого сначала преобразуем число 211₃ в десятичное, записав его развернутую форму:

211₃ = 2 ⋅ 3 2 + 1 ⋅ 3 1 + 1 ⋅ 3 0 = 18 + 3 + 1 = 22₁₀.

Затем переведем десятичное число 22₁₀ в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:

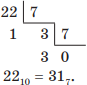
Примеры решения задач

Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.

Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 12₁₀ = 110_n = 0 ·n 0 + 1 · n 1 + 1 · n 2 . Составим уравнение: n 2 + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 110₃ = 0· 3 0 + 1 · 3 1 + 1 · 3 2 = 0 + 3 + 9 = 12 .

Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.

Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 22₁₀ = 34₆ = 24₉ = 14₁₈.

Ответ: 6, 9, 18.

Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.

Решение. Для удобства воспользуемся восьмеричной системой счисления. 101₂ = 5₈. Тогда число х можно представить как x = 5 · 8 0 + a₁ · 8 1 + a₂ · 8 2 + a₃ · 8 3 + . , где a₁, a₂, a₃, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 8 2 > 25), т. е. такие числа должны иметь представление x = 5 + a₁ · 8. Поскольку x ≤ 25 , допустимыми значениями a₁ будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:

a₁ = 0; x = 5 + 0 · 8 = 5;.

a₁=1; x = 5 + 1 · 8 = 13;.

a₁ = 2; x = 5 + 2 · 8 = 21;.

Ответ: 5, 13, 21.

Арифметические операции в позиционных системах счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0 ⋅ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ⋅ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ⋅ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ⋅ 1 = 1

Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.

Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:

Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:

Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:

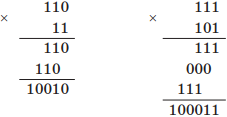
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.

Например, выполним сложение восьмеричных чисел 36₈ и 15₈, а также вычитание шестнадцатеричных чисел 9С₁₆ и 67₁₆:

При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.

Представление чисел в компьютере

Формат с фиксированной запятой

В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно

1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для п-разрядного представления диапазон будет составлять от 0 до 2 n – 1.

Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.

Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2 n − |А|.

Алгоритм получения дополнительного кода отрицательного числа:

1. Записать прямой код числа в п двоичных разрядах.

2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)

3. Прибавить единицу к полученному обратному коду.

Например, получим дополнительный код числа –2014₁₀ для шестнадцатиразрядного представления:

Прямой код	Двоичный код числа 201410 со знаковым разрядом	1000011111011110
Обратный код	Инвертирование (исключая знаковый разряд)	1111100000100001
Прибавление единицы	1111100000100001 + 0000000000000001
Дополнительный код	1111100000100010

При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.

1) Найдем разность 13₁₀ – 12₁₀ для восьмибитного представления. Представим заданные числа в двоичной системе счисления:

Запишем прямой, обратный и дополнительный коды для числа –12₁₀ и прямой код для числа 13₁₀ в восьми битах:

1310	–1210
Прямой код	00001101	10001100
Обратный код	—	11110011
Дополнительный код	—	11110100

Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):

Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.

2) Найдем разность 8₁₀ – 13₁₀ для восьмибитного представления.

Запишем прямой, обратный и дополнительный коды для числа –13₁₀ и прямой код для числа 8₁₀ в восьми битах:

810	–1310
Прямой код	00001000	10001101
Обратный код	—	11110010
Дополнительный код	—	11110011

Вычитание заменим сложением:

В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:

11111011 – 00000001 = 11111010.

Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –5₁₀.

Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2 n–1 , а максимальное: |А| = 2 n–1 или А = –2 n–1 – 1.

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно

А = –2 31 = –2147483648₁₀.

Максимальное положительное число равно

А = 2 31 – 1 = 2147483647₁₀.

Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.

Формат с плавающей запятой

Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.

Число в экспоненциальном формате представляется в таком виде:

где $m$ — мантисса числа (правильная отличная от нуля дробь);

$q$ — основание системы счисления;

$n$ — порядок числа.

Например, десятичное число 2674,381 в экспоненциальной форме запишется так:

2674,381 = 0,2674381 ⋅ 10 4 .

Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.

Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.

Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 1111111₂ = 127₁₀. Так как числа представляются в двоичной системе счисления, то

Аналогично, максимальное значение мантиссы равно

Таким образом, диапазон чисел обычной точности составляет $±1.7 · 10^$.