Шифр Виженера

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Касиски экспертиза

В 1863 году Фридрих Касиски первым опубликовал успешную общую атаку на шифр Виженера. [17] Более ранние атаки основывались на знании открытого текста или использовании узнаваемого слова в качестве ключа. У метода Касиски таких зависимостей не было. Хотя Касиски первым опубликовал отчет об атаке, очевидно, что другие знали об этом. В 1854 году Чарльза Бэббиджа подстрекали взломать шифр Виженера, когда Джон Холл Брок Туэйтс представил «новый» шифр в Журнал Общества искусств. [18] [19] Когда Бэббидж показал, что шифр Туэйтса был, по сути, просто еще одним воссозданием шифра Виженера, Туэйтс бросил вызов Бэббиджу: учитывая исходный текст (из Шекспира Буря : Акт 1, сцена 2) и его зашифрованную версию , он должен был найти ключевые слова, которые Туэйтс использовал для шифрования исходного текста. Бэббидж вскоре нашел ключевые слова: «два» и «вместе». Затем Бэббидж зашифровал тот же отрывок из Шекспира, используя разные ключевые слова, и предложил Туэйтсу найти ключевые слова Бэббиджа. [20] Бэббидж никогда не объяснял метод, который он использовал. Изучение записей Бэббиджа показывает, что он использовал метод, позже опубликованный Касиски, и предполагает, что он использовал этот метод еще в 1846 году [21].

Исследование Kasiski , также называемый тестом Kasiski, использует тот факт , что повторяющиеся слова, случайно, иногда зашифровано с использованием тех же ключевыми букв, что приводит к повторяющимся группам в шифротексте. Например, рассмотрим следующее шифрование с использованием ключевого слова ABCD :

В зашифрованном тексте легко заметить повторение, поэтому тест Касиски будет эффективным.

Расстояние между повторениями CSASTP равно 16. Если предполагается, что повторяющиеся сегменты представляют одни и те же сегменты открытого текста, это означает, что длина ключа составляет 16, 8, 4, 2 или 1 символ. (Все факторы расстояния являются возможными длинами ключей; ключ длины один — это просто простой шифр Цезаря , и его криптоанализ намного проще.) Поскольку длины ключей 2 и 1 нереально короткие, нужно пробовать только длины 16, 8 или 4. Более длинные сообщения делают тест более точным, потому что они обычно содержат больше повторяющихся сегментов зашифрованного текста. Следующий зашифрованный текст состоит из двух повторяющихся сегментов:

Расстояние между повторениями VHVS равно 18. Если предполагается, что повторяющиеся сегменты представляют одни и те же сегменты открытого текста, это означает, что длина ключа составляет 18, 9, 6, 3, 2 или 1 символ. Расстояние между повторами QUCE — 30 знаков. Это означает, что длина ключа может составлять 30, 15, 10, 6, 5, 3, 2 или 1 символ. Путем пересечения этих наборов можно было с уверенностью заключить, что наиболее вероятная длина ключа равна 6, поскольку 3, 2 и 1 нереально короткие.

Квадрат Полибия

Древние греки придумали если не все, то очень многое, в том числе и слово «криптография» (с древнегреческого «скрытый» + «пишу»). Среди множества способов передать сообщение тайно особо выделяется способ, названный именем выдающегося древнегреческого историка II в. до н. э. Полибия, который описал его в своем труде «Всеобщая история» . Для шифрования используется квадрат 6×6, в который вписываются все буквы алфавита. Каждый вертикальный и горизонтальный столбец получает свой порядковый номер, чтобы буквы, вписанные в ячейки квадрата, имели свои координаты (например, буква «А» — 11, «Б» — 12 и т. д.).

Для начала шифрования сообщения нужно найти в квадрате каждую букву шифруемого слова и заменить ее на расположенную под ней букву в том же столбце . Полученное в результате зашифрованное сообщение можно было записать как в виде цифр (сначала указывался номер горизонтальной строки, потом — номер вертикального столбца), так и в виде букв.

Интересный факт: изначально квадрат Полибия выполнял две функции: с его помощью можно было как зашифровать сообщение, так и передать его на дальнее расстояние посредством оптического телеграфа. Делалось это при помощи группы факелов: сначала поднимались факелы слева, количество которых указывало номер строки, а потом — факелы справа, указывающие номер столбца. Для получения и расшифрования такого сообщения адресату нужно было иметь точно такой же квадрат, а также зорко следить за количеством поднятых факелов.

Проверьте себя: «Телеграфируем» фразу «ОЧШОУеЗЗОУК» (34 51 52 34 43 21 23 23 34 43 26)

Исследовательские работы и проекты

Шифр Виженера – метод полиалфавитного шифрования буквенного текста с использованием кодового слова. Этот шифр прост для понимания и реализации, но на протяжении трех столетий он не поддавался взлому. По этой причине он получил название «неразгаданный шифр». Этот метод является простой формой многоалфавитной замены.

Впервые Шифр Виженера описал Джовани Баттиста Белласо, однако по ошибке был приписан другому имени, Блезу Виженеру, французскому дипломату. В 1518 году в развитии криптографии был сделан новый шаг. Аббат Иоганнес Тритемий, настоятель монастыря в Вюрцбурге, написал книгу «Полиграфия», в которой описывается ряд шифров.

Один из них использует «таблицу Тритемия» (более известна как «таблица Виженера») и развивает идею многоалфавитной замены. Система шифрования следующая: первая буква исходного текста шифруется по первой строке, вторая по второй и т.д. После использования последней строки следующая буква снова шифруется по первой строке. В шифре Тритемия отсутствует ключ, секретом является сам способ шифрования.

Далее за развитие криптографии принялся итальянец Джованни Белазо. В 1553 году он выпустил брошюру «Шифр синьора Белазо». В этом шифре ключом является фраза или слово. Пароль записывался периодически над буквами открытого текста. Буква пароля, стоящая над соответствующей буквой открытого текста, указывала номер строки в таблице Тритемия, по которой следует проводить замену (шифрование) это буквы.

Следующим составляющим звеном в нынешнем шифре Виженера стал соотечественник Белазо Джованни Батиста Порта. Он предложил отказаться от алфавитного порядка следования букв в первой строке таблицы Тритемия и заменить этот порядок на некоторый произвольный, являющийся ключом шифра. Строки таблицы по-прежнему циклически сдвигались. В своей книге «О тайной переписке», (вышедшей в 1563 году) Порта предложил биграммный шифр, а также привел описание механического дискового устройства, реализующего биграммную замену.

Далее в середине XVI века в Италии появляется книга Дж. Кардано «О тонкостях» с дополнением «О разных вещах». Там нашли отражение новые идеи криптографии: использование части самого передаваемого открытого текста в качестве ключа шифра (идея «самоключа») и новый способ шифрования, который вошел в историю как «решетка Кардано».

На рисунке №3 представлен сам шифр Кардано. Записка гласит: «Сэр Джон высоко ценит Вас и снова повторяет, что все, что доступно ему, теперь ваше, навсегда. Может ли он заслужить прощение за свои прежние промедления посредством своего обаяния», шифрованное послание: «В мае Испания направит свои корабли на войну».

Посол Франции в Риме Блез де Виженер, познакомившись с трудами Тритемия, Белазо, Кардано, Порта, Альберти, также увлекся криптографией. В 1585 году он написал «Трактат о шифрах», в котором излагаются основы криптографии.

По смыслу, Шифр Виженера состоит из нескольких шифров Цезаря (в данном шифре каждая буква сдвигается на несколько позиций).

• Исходный текст: «В кабинете информатики много компьютеров»
• Ключ: «Лимон»
• Полученный шифр: «н умпцщняу цщэыяълыхщц шцысь цчщюййысяьн»

То есть, шифрование происходит по формуле cj =(mj+kj)*mod n

Расшифровка происходит при помощи той же таблицы Виженера и формул. cj =(mj+n-kj)*mod n

В данных формулах n – количество букв в алфавите, mj — буквы открытого текста, kj – буквы ключа.

Предупреждение к методу

Шифр Виженера, как и многие другие, не является надежным, поскольку его легко взломать. Если есть необходимость передать секретную информацию, не нужно прибегать к использованию данного метода. Для таких целей разработаны другие методы. Шифр Виженера является одним из самых старых и популярных методов шифрования.

В качестве ключа выступает специальная фраза. Она несколько раз повторяется и пишется над шифруемым текстом. В результате каждая буква посылаемого сообщения сдвигается относительно заданного текста на определенное число, которое задается буквой ключевой фразы. На протяжении нескольких веков данный метод устойчиво занимал позицию самого надежного метода шифрования. В 19 веке отмечены первые попытки взлома шифра Виженера, которые основывались на определении длины ключевой фразы. Если известна ее длина, то текст можно разбить на определенные фрагменты, которые кодируются одним и тем же сдвигом.

Тест Касиски и определение с его помощью длины ключа

Чарльз Беббидж был первым, кто разработал алгоритм атаки на шифр Виженера в 1854 году. Стимулом к разработке алгоритма послужил обмен письмами с Джоном Х. Б. Твейтсом. Он заявил, что создал новый шифр, и отправил его в «Journal of the Society of the Arts»; когда Беббидж показал, что шифр Твейтса является лишь частным случаем шифра Виженера, Твейтс предложил ему его взломать. Беббидж расшифровал текст, который оказался поэмой «The Vision of Sin» Альфреда Теннисона, зашифрованной ключевым словом Emily — именем жены поэта. Но он не опубликовал свое открытие. Поэтому данный алгоритм назван в честь Фридриха Вильгельма Касиски, офицера прусской армии, который независимо от Беббиджа разработал такой же алгоритм в 1863 году. И только в XX веке, когда ученые исследовали заметки Беббиджа, появилась информация о первом изобретателе этого алгоритма. [12]

Эмпирически проверено, что индекс совпадения длинных осмысленных английских текстов, таких как «Моби Дик» Меллвила, приблизительно равен 0,065. При этом, конечно, в тексте оставляют только 26 букв английского алфавита. В то же время абсолютно случайный достаточно длинный текст на 26 буквах, в котором все буквы встречаются приблизительно одинаковое число раз, равен 0,038. Замечено, что чем «осмысленнее» текст, тем выше его индекс совпадения. Это обстоятельство как раз и помогает вычислять длину ключа в шифре Виженера.

Это может свидетельствовать о том, что длина ключа равна t , хотя и может оказаться ложным следом.

Если индекс совпадения некоторого языка неизвестен, то использование теста Касиски также возможно. Нужно не сравнивать полученные значения индексов совпадения со стандартным значением, а смотреть, когда этот индекс резко возрастет. Это может сигнализировать о найденной длине ключа. Конечно, речь идет о расшифровке осмысленных и одновременно достаточно длинных текстов. Впрочем, понятие осмысленности для формальных языков — понятие непростое.

Однако вернемся к шифру Виженера. Пусть определили правильно длину ключа, равную t . Теперь нужно найти сам ключ.

Гистограмма, построенная по стандартным частотностям букв в языке, имеет свои отличительные особенности. Они объясняются крайне неравномерным использованием букв в английском языке. Эта неравномерность как раз и позволяет эффективно применять частотный анализ.

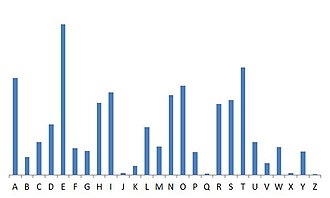
Прежде всего, обращают на себя внимание «пики», соответствующие буквам A, E, H, I, N, O, R, S, T, и «пеньки», соответствующие J, Q, X, Z. При этом некоторые «пики» стоят рядом, даже есть целая тройка: R, S, T. Все вместе дает весьма специфический рельеф.

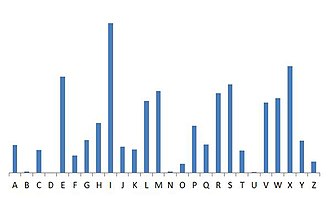
Если используется сдвиг на 4, то картина изменяется циклически. Наблюдается циклический сдвиг рельефа на 4 единицы. Если не знать величину сдвига, то её нетрудно восстановить, руководствуясь здравым смыслом.

Роторные машины

Частотный анализ

Как только длина ключа становится известной, зашифрованный текст можно записать во множество столбцов, каждый из которых соответствует одному символу ключа. Каждый столбец состоит из исходного текста, который зашифрован шифром Цезаря; ключ к шифру Цезаря является всего-навсего одним символом ключа для шифра Виженера, который используется в этом столбце. Используя методы, подобные методам взлома шифра Цезаря, можно расшифровать зашифрованный текст. Усовершенствование теста Касиски, известное как метод Кирхгофа, заключается в сравнении частотности появления символов в столбцах с частотностью появления символов в исходном тексте для нахождения ключевого символа для этого столбца. Когда все символы ключа известны, криптоаналитик может легко расшифровать шифрованный текст, получив исходный текст. Метод Кирхгофа не применим, когда таблица Виженера скремблирована, вместо использования обычной алфавитной последовательности, хотя тест Касиски и тесты совпадения всё ещё могут использоваться для определения длины ключа для этого случая. [13]

Дополнительные методы расшифровки

Раскрыть исходное сообщение можно с помощью метода частотного анализа, если заданный текст достаточно длинный. Разгадка шифра во многом сводится к поиску длины ключевой фразы. Существуют два основных метода, которые позволяют определить длину ключевой фразы. Первый метод раскодирования шифра Виженера разработал Фридрих Касицкий. В основе данного метода лежит поиск биграмм. Его суть заключается в том, что если в закодированном сообщении повторяется одна и та же биграмма на расстоянии, которое кратно длине ключевой фразы, то существует большая доля вероятности, что она встретится на тех же позициях в зашифрованном тексте. Если найти данное расстояние, получить его делители, можно получить набор определенных чисел. Именно они и будут составлять длину ключевой фразы. Однако данный метод требует некоторой доли везения. В большом закодированном тексте можно найти случайные биграммы, что значительно усложнит процесс расшифровки.

Второй метод по расшифровке текста предложил Фридман. Его суть заключается в циклическом сдвиге закодированного сообщения. Полученный текст записывается под оригинальным зашифрованным текстом и подсчитывается количество совпавших букв в нижней и верхней строке. Полученные числа позволяют вычислить так называемый индекс совпадений. Он определяется соотношением совпадений к общей длине сообщения. Индекс совпадения для русских текстов составляет примерно 6%. Однако для случайных текстов данный индекс составляет приблизительно 3 или 1/32. Метод Фридмана основывается на данном факте. Закодированный текст записывается со сдвигом в 1,2,3 и т.д. позиций. Затем для каждого сдвига необходимо вычислить индекс совпадений. Таким образом, необходимо произвести циклический сдвиг всего сообщения. При сдвигании индекса на определенное количество символов его длина может резко увеличиться. Это говорит о том, что длина ключевого слова может приравниваться к определенному числу. Если происходит ситуация, при которой все символы сдвигаются на одну и ту же позицию, индекс совпадения будет иметь такое же значение, как и исходный текст. Если вычисляется индекс для шифра Виженера, в любом случае происходит сравнение фактически случайного текста.