Шахматные задачи на тактику

Шахматные задачи в 1 ход для детей

Даже если вы не мечтаете сделать из своего ребенка чемпиона по шахматам, предложить ему шахматные задачи в картинках в один-два хода лишним не будет. Это еще один вид упражнений на внимательность, сообразительность и логику. В чем суть шахматных задач и как их решать? Разберемся вместе.

Как правило, это малофигурные задачи в один-два хода, не требующие серьезной подготовки. Цель — поставить мат королю или провести шахматную комбинацию.

Если вы сами не умеете играть в шахматы, не страшно — базовые принципы игры можно найти в интернете, а углубленные знания в данном случае не понадобятся.

Уделяйте внимание практике: ребенок заскучает от долгого разжевывания теории и станет рассеянным, поэтому все, что объясняете, сразу же демонстрируйте на примерах. Некоторые рекомендуют для наглядности показывать правила игры на реальной шахматной доске с настоящими фигурами, но в большинстве случаев достаточно и картинки на экране компьютера.

Не утомляйте ребенка. Дошкольнику не стоит давать более 10 задач подряд.

Отзывы о навыке Алисы — Шахматные задачи на тактику

Голос юмора или же Шутоголос в любой момент вас развеселит, не даст заскучать. А когда вам будет грустно — он расскажет вам обнадеживающую историю. В общем, не бот, а чудо!

Шахматная тактика для начинающих

ChessKingразработали его на основе книги Сергея Иващенко «Учебник шахматных комбинаций». 1275 упражнений для тренировки по двенадцати темам. Занимайтесь сразу по всем или выбирайте в настройках и прорабатывайте конкретное направление: учиться делать двойной шах, мат ферзем, «съедать коня» и осваивать другие игровые ходы. Проходите те упражнения, где раньше допустили ошибку. Сложность заданий рассчитывается от десяти до девяноста.

Пока решаете задачу, компьютер будет подсказывать, насколько правильным был ваш ход в конкретной ситуации. Есть функция пошагового анализа игры. Оформлена программа просто и со вкусом. Полмиллиона скачиваний. Рейтинг 4,7.

Шахматная задача со слоном

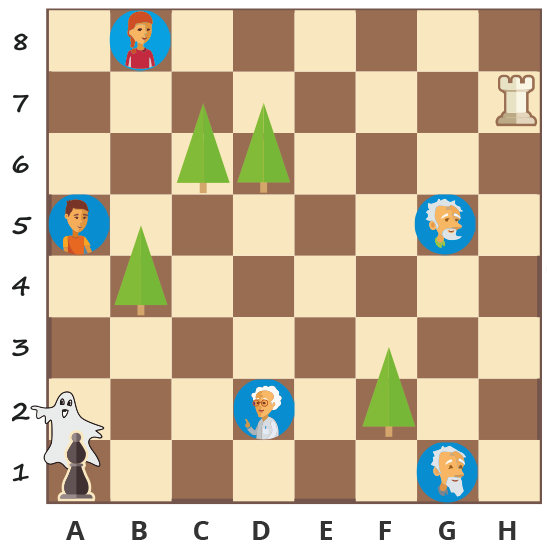
Условие: В праздник Хэллоуин шахматный Слон облачился в привидение, чтобы испугать своих знакомых: Профессора, Алису, Юру, Правдиша и Вруниша.

Правила:
1. Слон не может наступать на елки и перепрыгивать через них.
2. Слон не может стать на клетки, где его может сбить Ладья.
3. Чтобы испугать героя, Слон должен наступить на клетку с его изображением.

Вопрос: Какое наименьшее количество ходов Слону нужно сделать, чтобы испугать всех персонажей, до которых он может «дотянуться»?

Комментарий:
Важно учитывать, что Ладья не дает возможности Слону подойти к полям B8 и G1.

Задачу можно упростить: сначала «снять с доски» персонажей, которых Слон испугать не сможет.

Попытка третья: программирование

Теперь моя задача обрела иную форму: найти позиции на выходе из дебюта, которые мой брат (далее PlayerX) с наибольшей вероятностью достигнет, оказавшись при этом в невыгодном положении. Учтите, что никто из нас не является экспертом в игре, и что игроки нашего уровня играют не очень аккуратно.

Единственный способ противостоять хорошему игроку – это в точности следовать ходам из книги, потому что тогда вы по крайней мере знаете, что противник не сделает какой-либо ход, получив преимущество. Однако ситуация меняется, когда вы играете против игрока клубного уровня. Вы можете идти на риски (т.е. временно оказываться в невыгодном положении), если знаете, что противник вряд ли сможет на это правильно среагировать, в связи с чем окажется в затруднительном положении.

У меня также был список из более, чем 500 игр, которые брат сыграл на chess.com. А так как я программист, то естественным подходом для меня стало решить эту задачу инженерным путем.

Я начал скачивать сыгранные им партии с помощью API chess.com и разделять их на игры белыми и черными. Далее я сосредоточился на партиях, где брат играл за черных, потому что чувствовал, что имею больше шансов направить игру в нужное мне русло при игре за белых.

Далее я сформулировал задачу так: «Учитывая все позиции, которые видел PlayerX, какие из них по завершению дебюта скорее всего окажутся для него наименее выгодными?».

На этот раз задача была четко определена, и работа пошла уже в знакомой мне области. Я решил провести анализ в Python, а именно в блокноте Jupyter, потому что цели создавать переиспользуемый инструмент у меня не было, и нужно было лишь изучить доступные данные для нахождения одного решения.

Оказалось, что в Python уже есть отличные библиотеки для работы с шахматами: python-chess (генерация ходов, оценка и визуализация) и python stockfish (привязки для оценки шахматной позиции с помощью известного шахматного движка Stockfish).

Я преобразовал задачу в граф таким образом: узел – это частная шахматная позиция (описанная в нотации FEN). Ребро связывает два узла при том, что целевая позиция оказывается достижима из исходной путем допустимого хода. Для всех игр есть один одинаковый стартовый узел: начальная позиция.

Затем я построил граф всех партий, сыгранных PlayerX за черных, дополнительно обозначив каждое ребро количеством раз, которое был совершен соответствующий ход.

В итоге получился взвешенный направленный граф (не дерево, потому что позицию можно получить различной последовательностью ходов) типа такого (синтетического, потому что реальный бы просто сюда не уместился):

Здесь начальная позиция обозначена квадратным узлом, цвет указывает, чей в этой позиции ход: белых или черных.

Я также хотел получить оценку каждой позиции в плане преимущества белых, для чего использовал Stockfish. Учитывая, что процесс оценки тысяч позиций требует времени, я решил выполнить его отдельно и создал объект JSON, сопоставляющий каждую уникальную позицию FEN с ее оценкой Stockfish.

Оценка преимущества возвращалась в сантипешках или как «мат в X ходов», где положительное число означает преимущество белых, а отрицательное преимущество черных:

100 сантипешек означают преимущество перед оппонентом в одну пешку, а 300 в одну легкую фигуру вроде слона. Однако стоит обратить внимание, что Stockfish присваивает фигурам значение в зависимости от их позиции, значит вполне возможно иметь преимущество в 1000 сантипешек даже при равнозначном количестве фигур на доске.

Мне нужно было отобразить эту оценку во что-то более удобное для обработки, например в числа между 0 и 1. Для этого я навскидку решил, что преимущество в 300+ будет отображаться в 1.0, а отставание в 300+ в 0. Помимо этого, любой мат в X ходов (даже если X равен 20) будет 1 или 0.

Теперь вся информация была не месте, и мне оставалось найти узлы графа (т.е. позиции), в которых черные находились в проигрышном положении, а также наиболее подходящие для их достижения последовательности ходов. Нужно было взвесить ребра таким образом, чтобы стало возможным легко вычислять вероятность достижения конкретной позиции. Я рассуждал так:

• В каждой позиции можно оценить вероятность совершения конкретного хода путем деления количества проходов по соответствующему ребру на общее количество ходов, выполненных из этой позиции.
• Теперь каждое ребро будет иметь вес между 0 и 1, где более высокое значение отражает более высокую вероятность прохода по нему из этой позиции.
• Тогда вероятность прохождения конкретного пути будет произведением вероятностей всех пройденных ребер.

• Они представляли расстояние, а не вероятность (т.е. чем больше расстояние, тем ниже вероятность выбора пути).
• Расстояние между двумя узлами являлось суммой весов пройденных ребер (в противоположность произведению вероятностей).

В Python это будет выглядеть так:

Логарифмирование вероятности выбора ребра даст отрицательное число, потому что вероятность находится между 0 и 1. При этом не стоит беспокоиться о случае, когда вероятность равна нулю (в результате чего логарифмирование бы дало минус бесконечность), поскольку каждое ребро графа было пройдено не менее одного раза. Чем меньше вероятность, тем более отрицательным получится логарифм, значит инвертирование его знака даст то, что нам нужно, так как:

• Сумма логарифмов равна логарифму произведения их аргументов: log(a) + log(b) = log(a*b) .
• Чем больше результат, тем ниже определяющая его вероятность.

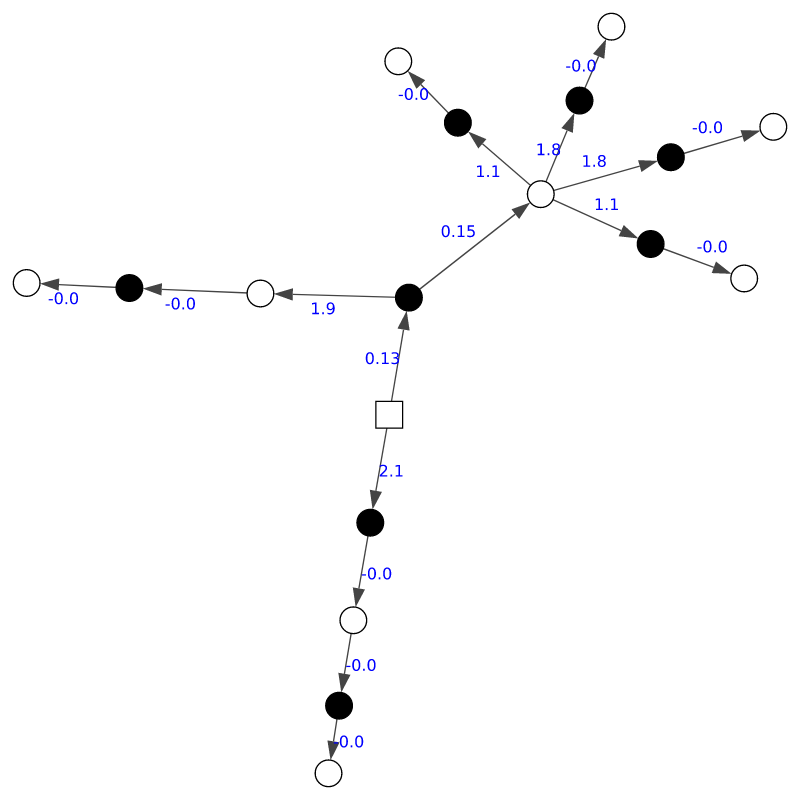
Вооружившись этой идеей, можно вычислить кратчайший путь между стартовым узлом и всеми другими узлами, используя алгоритм Дейкстры. В результате получится сопоставление между каждым узлом и кратчайшим путем до стартовой позиции, представляющее наиболее вероятную ведущую к ней последовательность ходов.

В этот момент я произвольно выбрал минимальное значение преимущества и упорядочил пути по вероятности. Первые несколько путей представляли для меня наибольший шанс выйти из дебюта с преимуществом перед PlayerX.

Доработки

Что я выяснил? Среди выданных этим алгоритмом позиций была следующая (ход белых):

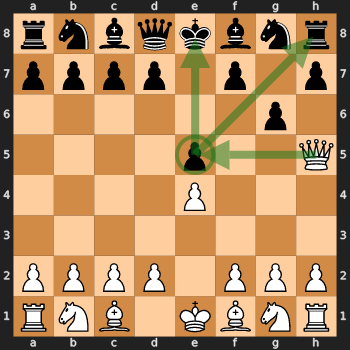
Как видите, черные находятся в очень неловком положении (+8.9 согласно Stockfish), потому что g6, последний ход черных, был ошибкой. Белые продолжат, забирая пешку с e5 и ладью. На этом партия для черных практически закончена, так как спасать им придется коня, пешку на h7 и слона. Еще один результат алгоритма был таким (ход белых):

Здесь мы видим мат в один ход (детский мат).

Проблема в том, что эти ошибки PlayerX совершал только несколько раз в своих первых партиях и больше не повторял. Ранние атаки ферзем обычно делают только неопытные игроки, и эффективны они только против игроков того же уровня. Выйдя из разряда начинающих, PlayerX уже долгое время не совершал этих ошибок, потому что более грамотные противники так не ходят. Я знал, что такой дебют использовать не получится, поскольку PlayerX умел против него защищаться.

Еще одна проблема была связана с последовательностями ходов, которые происходили только раз, но из типичных позиций. Вероятность их заключительной позиции оказывалась такой же, что и вероятность последней типичной позиции, потому что каждое ребро имело вероятность 1.0 (учитывая, что другие возможности не разыгрывались). В примере ниже можно проследовать по ребрам 7 и 6 (наиболее распространенная позиция на втором ходу), а затем по одному из ребер с 1-ми. Далее все последующие ходы будут сыграны только раз (потому что данная позиция сложилась только в одном матче), в результате чего каждый ход будет иметь вероятность 1.0.

А вот и вероятности:

Такой схеме верить нельзя, потому что вряд ли однозначно будет сыграна одна и та же последовательность ходов. Для такого вывода у нас недостаточно игр, в которых игра бы происходила из этих позиций.

Известная цитата (Б. Брюстера?): «В теории нет разницы между теорией и практикой, а вот на практике есть» оказалась в этом случае верна, поэтому мне потребовались кое-какие доработки и самостоятельное исследование, чтобы найти более удачные предполагаемые позиции.

Вторую проблему я исправил, установив для вероятности ребра верхнюю границу, чтобы длинные последовательности ходов, сыгранные только раз, постепенно утрачивали свою вероятность.

Для первой же проблемы я просто вручную отфильтровал плохие предположения. В итоге у меня для проработки осталась всего пара позиций.

Причиной еще одной модификации стало то, что я не хотел, чтобы вероятности ходов белых влияли на вероятность выбора пути, потому что играл за белых и мог сам решать, каким путем идти. По этой причине я установил все вероятности ходов белых на 1.0 (нулевой вес), получив в результате такой граф:

Подготовка

В процессе изучения я остановил свой выбор на следующей позиции:

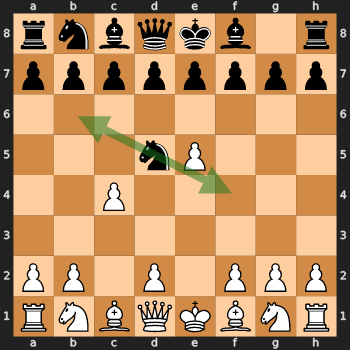
Согласно Lichess, это защита Алехина (атака двух пешек). В этой позиции для черных есть всего один удачный ход (Nb6), после которого они все равно остаются в менее выгодном положении (+0.6 согласно Stockfish). Однако из этой позиции PlayerX зачастую играет на Nf4, что весьма для него неудачно (+2.3). Я создал на Lichess студию и начал просматривать несколько вариаций (хороших ходов и ходов, сыгранных PlayerX).

В конечном итоге получилось дерево возможностей, которое я постарался запомнить и понять. К примеру, мне нужно было узнать, чему угрожал ход вроде d5, почему ход Nf4 был неудачным, и подготовить на все оптимальные ответы.

Занимался я этим недолго, потому что мне быстро надоело, и подготовился по факту лишь частично.

Не зарегистрированы?

Нажмите здесь для регистрации, и начните играть в шахматы прямо сейчас! Не требуется никакого дополнительного программного обеспечения, никакой оплаты. Вы получите онлайновую игру “Шахматы” в лучшем ее виде!

Присоединяйтесь к нам! Начните играть прямо сейчас! Сделайте свой ход!

Ход ладьи

Шахматная ладья ходит по горизонтали или вертикали. Даны две различные клетки шахматной доски, определите, может ли ладья попасть с первой клетки на вторую одним ходом. Программа получает на вход четыре числа от 1 до 8 каждое, задающие номер столбца и номер строки сначала для первой клетки, потом для второй клетки. Программа должна вывести YES , если из первой клетки ходом ладьи можно попасть во вторую или NO в противном случае.

Задача очень простая, чтобы решить достаточно представить себе ладью на шахматном поле и проанализировать ее ход. Ладья ходит только либо по вертикале вверх или вниз, либо по горизонтали влево или вправо. Становится ясно, что одна из координат клетки всегда остается неизменной, т.е. если ладья ходит по вертикале неизменна координата Х если по горизонтали то Y. Отсюда напишем условие при котором будем сравнивать если координаты X первой и второй клетки одинаковы или координаты Y первой и второй клетки одинаковы значит выводим YES – ладья может попасть с первой клетки на вторую, иначе – NO, не может.

Сложные шахматные задачи на логику

Шахматы не зря относят к логическим играм. Они действительно помогают развивать мышление в любом возрасте. Шахматные задачи — уникальная возможность самосовершенствования. Самые сложные головоломки, которые невозможно решить, не задействовав логическое мышление, — это:

1. Двухходовки. Сложные шахматные задачи на мат в 2 хода. Несмотря на малое количество ходов, они часто оказываются даже труднее, чем многоходовые композиции и этюды.
2. Сложные шахматные задачи в 1 ход. Необходимо передвинуть одну из имеющихся на доске фигур, чтобы победить. Но какую именно и куда — вопрос, ответ на который найти порой весьма сложно. Даже опытные игроки считают, что в шахматах задачи на мат сложные.

Средний уровень

Теперь нужно уделить особое внимание ходам соперника, так как каждое перемещение фигуры по полю является частью определенной комбинации. Подстраивайтесь под стратегию противника. Участвуйте в размене фигур, особенно, когда это идет вам на пользу.

На этом этапе игры в шахматы следует продумывать комбинацию уже на 6 шагов.

Сначала это покажется слишком сложным, но вскоре принесет свои плоды. Теперь схема как выиграть в шахматы будет иметь три главных составляющих. Первая – выведите вперед больше фигур. Вторая – не упускайте из виду центр поля. Третья – не оставляйте короля без защиты и путей отступления.

Гроссмейстеры играют партию в быстрые шахматы, где фигурами являются живые люди

Рекомендуем для изучения