Реферат на тему: Системы счисления

Учитель информатики

Информатика. 8 класса. Босова Л.Л. Оглавление

Ключевые слова:

• система счисления
• цифра
• алфавит
• позиционная система счисления
• основание
• развёрнутая форма записи числа
• свёрнутая форма записи числа
• двоичная система счисления
• восьмеричная система счисления
• шестнадцатеричная система счисления

История создания систем счисления

В древние времена людям приходилось рассчитывать на пальцы. Кроме пальцев, нужно было пересчитать много предметов, на счет было записано больше предметов. Один считал единицы, второй — дюжины, третий — сотни. Очевидно, что такой расчет лег в основу принятой почти всеми народами системы вычислений, называемой десятичной системой. Расчет с базовой десяткой также применим к восточным славянам.

Там, где ты ходил босиком, можно было легко сосчитать до 20 на пальцах. Следы использования при подсчете базовой двадцатки сохранились. Например, во французском языке цифра 80 в буквальном переводе на русский звучит как «четырежды двадцать».

Перепись также была разделена на десятки, т.е. перепись по системе с базой 12. Его происхождение связано с 12 фалангами на четырех пальцах руки (кроме большого пальца). Даже сейчас некоторые пункты все еще считаются десятками. Столовые приборы состоят из полдюжины или дюжины комплектов.

В древнем Вавилоне, где математика была очень сложной, существовала очень сложная шестнадцатеричная система счисления. В настоящее время мы также используем эту систему. Например: 1 час=60 минут; 1 минута=60 секунд.

Самая старая из систем нумерации пальцев — шестнадцатеричная. Эта система родилась, и она наиболее распространена в Америке. Его происхождение относится к эпохе, когда человек считал на пальцах одной руки. До недавнего времени некоторые племена сохранили пятипальцевую систему счисления в чистом виде.

Таким образом, все системы (пять, двенадцатеричная, двадцать) связаны с тем или иным способом счета пальцами рук (или рук и ног). Переход человека к счету пальцев привел к созданию различных систем подсчета.

Единицы компьютерной информации

В предыдущем пункте уже говорилось о том, что бинарный код внутри компьютера хранится в виде комбинаций большого количества элементов, каждый из которых может иметь одно из двух состояний.

Такой мельчайший элемент, участвующий в формировании бинарного кода, называется битом.

Битом является, например, каждая темная или светлая точка дорожки оптического диска, каждая запоминающая ячейка оперативной памяти компьютера и т.д.

Чем больше битов содержит какой-то носитель, тем больше информации на нем можно закодировать. К примеру, оптический диск типа «CD» может содержать около 6 млрд. битов. Жесткий диск — в десятки раз больше.

Но каждый отдельный бит сам по себе не имеет практической ценности. Для кодирования информации используются блоки из нескольких битов.

Представим, например, что в каком-то запоминающем устройстве содержится только один бит. В нем можно будет закодировать всего одно из двух состояний чего либо, например, одну из двух цифр или один из двух цветов. Понятное дело, что практическая ценность такого носителя минимальна.

Блок из 2 битов может принимать одно из 4 состояний:

В 3-хбитном блоке можно закодировать уже одно из 8 состояний:

Ну а 8-битный блок может принимать аж 256 разных состояний. Это уже достаточно существенная частичка двоичного кода, позволяющая отобразить один из значительного количества вариантов.

Например, каждому состоянию 8-битного блока можно сопоставить какую-то букву. Вариантов, а их 256, будет достаточно для кодирования всех русских букв, включая строчные и прописные их варианты, а также всех знаков препинания. Заменяя каждую букву соответствующим 8-мибитным блоком, из двоичного кода можно составить текст.

Этот принцип и используется для записи в компьютере текстовой информации (подробнее речь об этом пойдет ниже).

Как видите, 8-битная ячейка имеет вполне реальную практическую ценность. Поэтому ее и решили считать минимальной единицей компьютерной информации. Эта единица получила название байт.

Текстовые файлы состоят из сотен, тысяч или даже десятков тысяч букв. Соответственно, для их хранения в двоичном коде требуются сотни, тысячи или десятки тысяч байтов.

Поэтому на практике гораздо чаще приходится имеет дело не с байтами, а с более крупными единицами:

• килобайтами (1 килобайт = 1024 байт);

• мегабайтами (1 мегабайт = 1024 килобайт);

• гигабайтами (1 гигабайт = 1024 мегабайт);

• терабайтами (1 терабайт = 1024 гигабайт).

Предварительный просмотр:

Муниципальное общеобразовательное учреждение

Ангеловская средняя общеобразовательная школа

по информатике и информационно-коммуникационным технологиям

Тема : «Системы счисления»

ученица 9 класса

Мунческу Лорина Валерьевна.

Шишкин Алексей Сергеевич.

На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Это был еще не счет, а лишь его зародыш.

Впоследствии способность различать друг от друга небольшие совокупности развивалась; возникли слова для обозначений понятий «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Наши пословицы сохранили память об этой эпохе («семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ» и т.д.).

Особо важную роль играл природный инструмент человека – его пальцы. Этот инструмент не мог длительно хранить результат счета, но зато всегда был «под рукой» и отличался большой подвижностью. Язык первобытного человека был беден; жесты возмещали недостаток слов, и числа, для которых еще не было названий, «показывались» на пальцах.

Поэтому, вполне естественно, что вновь возникавшие названия «больших» чисел часто строились на основе числа 10 – по количеству пальцев на руках.

На первых порах расширение запаса чисел происходило медленно. Сначала люди овладели счетом в пределах нескольких десятков и лишь позднее дошли до сотни. У многих народов число 40 долгое время было пределом счета и названием неопределенно большого количества. В русском языке слово «сороконожка» имеет смысл «многоножка»; выражение «сорок сороков» означало в старину число, превосходящее всякое воображение.

На следующей ступени счет достигает нового предела: десяти десятков, и создается название для числа 100. Вместе с тем слово «сто» приобретает смысл неопределенно большого числа. Такой же смысл приобретают потом последовательно числа тысяча, десять тысяч (в старину это число называлось «тьма»), миллион.

На современном этапе границы счета определены термином «бесконечность», который не обозначает какое либо конкретное число.

Современный человек в повседневной жизни постоянно сталкивается с числами и цифрами — они с нами везде. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах, начиная с вычислений учениками младших классов, выполняемых карандашом на бумаге, заканчивая вычислениями, выполняемыми на суперкомпьютерах. Поэтому эта тема для меня очень интересна, и мне захотелось узнать об этом больше.

3.2 Основные понятия машинной арифметики

В двоичной системе счисления используются только два символа, что хорошо согласуется с техническими характеристиками цифровых схем. Действительно очень удобно представлять отдельные составляющие информации с помощью двух состояний:

Отверстие есть или отсутствует (перфолента или перфокарта);

Материал намагничен или размагничен (магнитные ленты, диски);

Уровень сигнала большой или маленький.

Существуют специальные термины, широко используемые в вычислительной технике: бит, байт и слово.

Битом называют один двоичный разряд. Крайний слева бит числа называют старшим разрядом (он имеет наибольший вес), крайний справа – младшим разрядом (он имеет наименьший вес).

Восьмибитовая единица носит название байта.

Многие типы ЭВМ и дискретных систем управления перерабатывают информацию порциями (словами) по 8, 16 или 32 бита (1, 2 и 4 байта). Двоичное слово, состоящее из двух байт, показано на рис. 3.1.

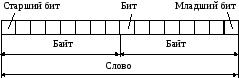
Рисунок 1.3.2 — Бит, байт и слово

Что такое система счисления в информатике?

Люди считают уже давно. Для этого мы используем системы, которые связывают уникальные символы с определенными значениями. Это называется числовой системой, и это метод, который мы используем для представления чисел и управления ими.

Система счисления должна иметь уникальные символы для каждого значения, быть последовательной, обеспечивать сопоставимые значения и легко воспроизводимой.

Вы, вероятно, больше всего знакомы с десятичной системой, которая лежит в основе того, как люди считают. Десятичная система имеет основание 10, потому что она предоставляет 10 символов для представления всех чисел:

Люди используют десятичную систему счисления, потому что у нас есть 10 пальцев, на которые можно рассчитывать, но машины не могут позволить себе такой роскоши. Итак, мы создали другие системы счисления, которые выполняют те же функции. Компьютеры представляют информацию иначе, чем люди, поэтому нам нужны разные системы для представления чисел.

Компьютеры поддерживают следующие системы счисления:

• Двоичный
• Восьмеричный
• Десятичный
• Шестнадцатеричный

Узкоспециальные устройства

Иногда для выполнения каких-то специфических задач действительно выгоднее разработать узкоспециализированное устройство, которое будет выполнять строго ограниченный набор логических операций, зато будет это делать во много раз быстрее.

Когда был бум майнинга криптовалют, в числе прочего разрабатывались и так называемые ASIC майнеры, выполненные в форм факторе небольшого устройства, подключаемого по USB и напоминающего большую флешку. На борту они несли специализированный чип, заточенный исключительно на вычисление хэшсумм. Таким образом некоторые люди майнили криптовалюту, подключив несколько десятков таких устройств к какой-нибудь Raspberry PI через USB хабы с внешним питанием.

Сейчас трендом является искусственное обучение и нейросети. Но только очень богатые корпорации могут себе позволить строить нейрокомпьютеры с нуля. Остальные используют для обучения нейросетей видеокарты или специальные внешние нейросопроцессоры. Существует такое устройство как Intel Movidius и выглядит тоже как большая флешка, точно так же подключается к любой машине по USB и позволяет использовать сопроцессор для глубокого машинного обучения в паре с сопутствующими библиотеками.

Так что если и появится в обозримом будущем троичный компьютер, то скорее всего в подобном форм-факторе, как внешний сопроцессор с набором сопутствующих библиотек, но не как отдельная полноценная система, по крайней мере изначально.

Формула возможных вариантов

В этом примере с помощью четырех бит мы смогли закодировать 16 информаций. А что будет если использовать пять бит? Сколько информации мы можем закодировать? Неужели нам придется опять перебирать варианты? Ну уж нет! Для этого есть простая формула.

Возможные варианты информаций= 2 N , где N — количество битов

Предположим, мы используем два бита, следовательно, мы можем закодировать 2 2 =2х2=4 информаций, то есть 4 возможных варианта, если же используем три бита, то 2 3 =2х2х2=8, значит 8 информаций мы можем закодировать с помощью трех битов и тд. Нетрудно посчитать, что с помощью пяти битов можно закодировать 2 5 =2х2х2х2х2=32. Все просто, не правда ли? А сколько информаций мы можем закодировать, если использовать 8 бит? Итак, 2 8 =2х2х2х2х2х2х2х2=256 информаций! Неплохо! Короче говоря, если наш воин, который носит варежки из мамонта, имел бы восемь рук, он смог бы показать с помощью них 256 всех комбинаций, и если бы они договорились, что какая-то комбинация — это столько то убитых человечков. :-). Жесть))) Кстати, как Вы прочитали из прошлой статьи, 8 бит = 1 Байт. Например, информация с кодом 1011 0111 (пробел между группами из 4 битов ставится для удобства) — это восемь бит или просто Байт.

ПРИНЦИП РАБОТЫ СУММАТОРА АРИФМЕТИЧЕСКОГО УСТРОЙСТВА

Предположим, что следует сложить два двоичных числа А = 1110 и Б = 1101. Сложение производится последовательно, разряд за разрядом, как при обычном счете.

Рис. 16-19. Схема триггера.

При сложении чисел первого разряда 0+1 в сумме получается 1; так же и при сложении чисел второго разряда 1 + 0 получается 1. При сложении чисел третьего разряда 1 +1 получается 2 . Следовательно, двойка, как единица, переносится в четвертый разряд или, как мы гов орим, ( единица в уме). Эта единица поставлена в строке переноса П , над числом А, Складывая четвертый разряд, получаем 3; половина двойки, т, в/1, идет и сумму С, а единица переноса переходит в сумму пятого разряда, где

С = П + А + Б = 1 + 0 + 0 = 1

Очевидно, устройство для суммирования — сумматор пpи последовательном суммировании, как это делалось, должен иметь два входа для чисел А и Б, вход для переноса П, выход для суммы С и выход для числа П, переносимого в следующий разряд. Блок-схема такого устройства, состоящего из запоминающего блока, однозарядного сумматора и устройства задержки (для переноса) на один разряд, показана на рис. 16-21.

Рис. 16-20. Работа двоичного счетчика.

Схема работы сумматора (рис. 16-22), осуществляется при помощи логических схем И, ИЛИ, НЕ. Для простоты все устройства заземления, форми рования импульсов, усиления их на рис. 16-22 не показаны. При разборе схемы необходимо вспомнить следующее.

Так как все схемы И, кроме И1, присоединены к положительному зажиму источника энергии Е_а, то через сопротивления r этих схем и внутреннее сопротивление источников сигналов проходит ток. Отрицательный зажим источников заземлен. Потенциал анодов этих схем невысок, так как значительная часть напряжения падает на сопротивлениях r. Импульсы высокого потенциала на анодах появляются только в те моменты, когда на все катоды приходят положительные импульсы напряжения, способные запереть вентили. Только тогда положительные импульсы схем И передаются дальше.

Через схемы ИЛИ положительный импульс проходит, если он подается хотя бы к одному аноду вентиля.

Схема НЕ заперта отрицательным потенциалом на сетке лампы. При этом потенциал ее анода высок, так как в ее анодном сопротивлении r ток не протекает. Этим потенциалом нормально заперт вентиль И1, и только в этом состоянии через его сопротивление г может пройти положительный импульс на выход С.

При появлении положительного импульса напряжения на сетке лампы она пропускает ток, потенциал на ее аноде падает и схема И1 открывается. В этом случае потенциал анода вентиля И1 при поступлении импульса от схемы ИЛИ1 будет низким, так как ток проходит через лампу схемы НЕ . Потенциал выхода С тоже, будет низким.

Рис. 16-21. Блок-схема работы сумматора.

Теперь можно рассмотреть процесс сложения двух предложенных выше чисел. Триггеры регистра суммы С запоминающего устройства (рис. 16-21) перед началом операции сложения ставятся на нуль. Устройство управления посылает периодически импульсы, которыми и управляется схема. За каждый период складываются цифры одного разряда.

В течение первого импульса из запоминающего устройства (рис. 16-21) выбираются цифры младшего разряда А = 0 и Б = 1. Другими словами, на вход Б сумматора (рис. 16-22) поступает импульс положительного потенциала, а на входе А его нет. Тогда импульс проходит схему ИЛИ 1, сопротивление r схемы И 1, ИЛИ 2, на выход Сив младшем разряде регистра запоминающего устройства суммы С триггер перебрасывается в положения 1. Вторым импульсом из запоминающего устройства выбираются цифры А = 1 и 5 = 0. Импульс через вход (рис. 16-22) проходит схему ИЛИ 1, И1, ИЛИ2 и попадает на выход С. Триггер второго разряда запоминающего устройства перебрасывается в положение 1 (рис. 16-21).

Ряс. 16-22. Схема работы сумматора.

Третий импульс выбирает из запоминающего устройства цифры А = 1 и Б = 1 и на входе сумматора А, Б получаются положительные импульсы. Тогда запирается схема И2 и выдает положительный импульс на схему ИЛИ3. Импульс проходит на схему задержки Я и на сетку лампы схемы НЕ. Лампа отпирается и начинает проводить ток. Диод схемы И 1 отпирается, импульсы А и Б через схему ИЛИ 1 и схему И 1 проходят через лампу схемы НЕ. Потенциал анода схемы И1 низкий и на выход С через схему ИЛИ 2 сигнал не поступает. Триггер третьего разряда С запоминающего устройства остается в положении 0.

Импульс напряжения на линии задержки задерживается до момента суммирования цифр четвертого разряда. Это равносильно тому, как человек держит единицу «в уме». Об устройстве линии задержки (З) будет сказано ниже.

В четвертый такт сложения, два импульса А, Б и импульс Я, выходящий из линии задержки, запирают схемы И2, И3, И4, которые через схему ИЛИ3 выдают второй импульс на схему задержки и схему НЕ. В этом случае, как уже указывалось, схемы ИЛИ 1 и И1 не выдают импульса на выход С. Однако поскольку схема И 5 заперта высоким потенциалом входа А, Б и первым импульсом схемы задержки П, то потенциал ее анодов становится высоким и через схему ИЛИ 2 на выход, в запоминающее устройство поступает импульс высокого напряжения. Происходит переброс триггера четвертого разряда в положение 1.

При пятом такте импульсы А, Б отсутствуют, но возникший импульс переноса при суммировании предыдущего разряда через линию задержки схемы ИЛИ 1, И 1, ИЛИ 2 выдается на выход С в пятый разряд сумматора. Триггер этого разряда записывает 1. Таким образом, просуммированы числа 1110 + 1101 = 11011 или в десятичной системе 14 + 13 = 27.

На рис. 16 -23 показан один из способов устройства линии задержки, Он основан на акустическом принципе. В стальную трубку 1, заполненную ртутью 2, вставлены две пластины из кварца 3, при помощи резиновых колец 4. Кварц имеет способность изменять свой объем при помещении его в изменяю щееся электрическое поле. Если на вход одной пластинки подать импульс напряжения, то он вызовет механические колебания самого кварца и ртути в трубке, которые, с определенной ско ростью, будут переданы другой кварцевой пластинке на выходе. Эти механические колебания кварц способен переобразовывать в электрические колебания на выходе. Скорость прохождения механических колебаний в ртути неизмеримо меньше скорости распространения электрических импульсов и поэтому электрический импульс передается с задержкой. Время задержки обычно составляет микросекунды. Меняя длину трубки, можно изменять время задержки.

Рис. 16-23. Устройство акустической линии задержки.

Статья на тему Двоичная система счисления

Похожие страницы:

Электрический разряд в газах это ионный поток который разделяется на три разновидности тихий искровой и дуговой, тихий можно наблюдать при.

Счетчик частиц это устройство для определения активности ионизирующего излучения любой природы. Существует несколько видов счетчиков, электронные и газоразрядные. Газоразрядные в.

Что такое электроемкость Конденсатор Это величина, характеризующая способность проводника воспринимать электрические заряды, называется его электроемкостью или просто емкостью. При сообщении уединенному от других.

Содержание статьи1 ГЕНЕРАТОРЫ1.1 Ламповый генератор синусоидальных колебаний1.2 Генераторы с кривой пилообразного напряжения1.3 Мультивибраторы ГЕНЕРАТОРЫ Ламповый генератор синусоидальных колебаний Переменные токи.

Содержание статьи1 Потенциал электрического поля и разность потенциалов1.1 Разность потенциалов1.2 Эквипотенциальные поверхности1.3 Что такое электрон-вольт Потенциал электрического поля и разность.

ГЕНЕРАТОР ЭЛЕКТРОДВИГАТЕЛЬ (Г—ЭД) Схема генератор — электродвигатель, показанная на рис. 8-41, дает возможность экономично, плавно и в широких пределах регулировать скорость вращения электродвигателя.