Расчет числа Пи

Как вычисляют число пи на компьютере

Самый простой и легкий в реализации метод.

Рассмотрим произвольный квадрат с центром в начале координат и вписанный в него круг. Будем рассматривать только первую координатную четверть. В ней будет находиться четверть круга и четверть квадрата. Обозначим радиус круга r, тогда четверть квадрата тоже будет квадратом(очевидно) со стороной r.

Будем случайным образом выбирать точки в этом квадрате и считать количество точек, попавших в четверть круга. Благодаря теории вероятности мы знаем, что отношение попаданий в четверть круга к попаданиям ‘в молоко’ равно отношению площадей — пи/4. Вот, собственно, и весь алгоритм. Чем больше взятых наугад точек мы проверим, тем точнее будет отношение площадей.

Вот простенькая программа на Паскале, считающая пи этим способом. Четыре первых знака требуют на моем PentiumII-300 около 5 минут.

Однако, как говорил Козьма Прутков, ‘нельзя объять необъятное’, что, в применении к данному случаю, можно перефразировать так: нельзя просуммировать бесконечное число слагаемых за конечное время, каким бы быстрым компьютером мы не располагали.

Слава Богу, этого и не требуется. Поскольку мы хотим найти не точное значение PI, а лишь его приближение с пятью верными десятичными знаками, нам достаточно просуммировать такое количество первых членов ряда, чтобы сумма всех оставшихся членов не превышала 10 -5 .

Остался, правда, открытым вопрос о том, сколько же все-таки членов ряда нужно просуммировать, чтобы получить результат с требуемой точностью?

Ответ на этот вопрос в ‘общем виде’ выходит далеко за рамки настоящего обсуждения. Это отдельная тема в курсах математического анализа и численных методов.

К счастью, данный конкретный ряд позволяет найти очень простое правило, позволяющее определить момент, когда следует прекратить суммирование. Дело в том, что ряд Грегори является знакопеременным и сходится равномерно (хотя и медленнее, чем хотелось бы). Это означает, что для любого нечетного n , сумма первых n членов ряда всегда дает верхнюю оценку для PI, а сумма n +1 первых членов ряда — нижнюю.

Значит, как только разница между верхней и нижней оценками окажется меньше, чем требуемая точность, можно смело прекращать вычисления и быть уверенным, что как та, так и другая оценки отличаются от истинного значения PI не более, чем на 10 -5 . В качестве окончательного результата разумно взять среднее значение между полученными верхней и нижней оценками. Таким образом, можно предложить алгоритм, приведенный ниже.

При реализации этого алгоритма на машине следует помнить, что ряд Грегори сходится достаточно медленно, и поэтому n может принимать довольно большие значения.

Для вычисления сколько-нибудь большого количества знаков пи предыдущий способ уже не годится. Но существует большое количество последовательностей, сходящихся к Пи гораздо быстрее. Воспользуемся, например, формулой Гаусса:

p	= 12arctan	1	+ 8arctan	1	— 5arctan	1
4		18		57		239

Доказательство этой формулы несложное, поэтому мы его опустим.

Расчет числа Пи

Число Пи — это математическая постоянная, равная отношению длины окружности к диаметру окружности.

Формула расчета числа Пи:

π = L / D, где

L — длина окружности;
D — диаметр окружности;

Для справки: π = 3.1415926535.

Смотрите также число Пи до сотого знака после запятой здесь.

Быстро выполнить этот математический расчет можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор для расчета числа Пи в зависимости от диаметра окружности и длины окружности. С помощью этой программы вы в один клик сможете вычислить число Пи, если известен диаметр окружности и её длина.

Число пи на клавиатуре и в Word

Существует несколько способов ввода числа Пи, как с клавиатуры компьютера, так и с помощью простого копирования. Опишем, как проще всего написать число Пи.

Способ — 1.
Вот символ числа Пи — π . Просто скопируйте его и вставьте в свой документ.

Способ — 2, для PC.
Нажмите клавишу Alt и не отпуская ее введите код символа числа π — «960» или «227«, отпустите «Alt«. Клавиша Alt находится в нижней части, как правило, слева и справа от клавиши «Пробел«. Цифровой код нужно вводить с помощью цифровой клавиатуры находящейся спава.

Способ — 3, для MAC
Нажмите клавишу «Option» и не отпуская клавишу «P«, появится символ числа Пи.

Способ — 4, получение числа Пи в Ворде или в другом текстовом редакторе
В Word-е, в окне выбора шрифта, выберите шрифт Symbol и нажмите букву «P«.

Способ — 5, таблица символов.
В операционной системе Windows необходимо открыть программу «Таблица символов«. Для этого воспользуйтесь меню «Пуск» — «Все программы» — «Служебные«. В таблице символов выбираем нужный нам шрифт и ищем символ числа Pi в огромном многообразии различных символов.

Кстати, не со всеми шрифтами символ числа Пи будет корректно отображаться. Лучше всего для этого подходит шрифт «Times New Roman«.

Вычисление N-го знака числа Пи без вычисления предыдущих

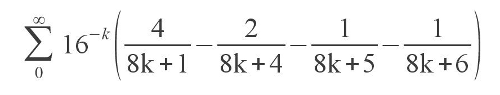
С недавних пор существует элегантная формула для вычисления числа Пи, которую в 1995 году впервые опубликовали Дэвид Бэйли, Питер Борвайн и Саймон Плафф:

Казалось бы: что в ней особенного — формул для вычисления Пи великое множество: от школьного метода Монте-Карло до труднопостижимого интеграла Пуассона и формулы Франсуа Виета из позднего Средневековья. Но именно на эту формулу стоит обратить особое внимание — она позволяет вычислить n-й знак числа пи без нахождения предыдущих. За информацией о том, как это работает, а также за готовым кодом на языке C, вычисляющим 1 000 000-й знак, прошу под хабракат.

Как же работает алгоритм вычисления N-го знака Пи?
К примеру, если нам нужен шестнадцатеричный знак числа Пи, мы домножаем всю формулу на 16^1000, тем самым обращая множитель, стоящий перед скобками, в 16^(1000-k). При возведении в степень мы используем двоичный алгоритм возведения в степень или, как будет показано в примере ниже, возведение в степень по модулю. После этого вычисляем сумму нескольких членов ряда. Причём необязательно вычислять много: по мере возрастания k 16^(N-k) быстро убывает, так что, последующие члены не будут оказывать влияния на значение искомых цифр). Вот и вся магия — гениальная и простая.

Формула Бэйли-Борвайна-Плаффа была найдена Саймоном Плаффом при помощи алгоритма PSLQ, который был в 2000 году включён в список Top 10 Algorithms of the Century. Сам же алгоритм PSLQ был в свою очередь разработан Бэйли. Вот такой мексиканский сериал про математиков.
Кстати, время работы алгоритма — O(N), использование памяти — O(log N), где N — порядковый номер искомого знака.

Думаю, уместно будет привести код на языке Си, написанный непосредственно автором алгоритма, Дэвидом Бэйли:

Какие возможности это даёт? Например: мы можем создать систему распределённых вычислений, рассчитывающую число Пи и поставить всем Хабром новый рекорд по точности вычисления (который сейчас, к слову, составляет 10 триллионов знаков после запятой). Согласно эмпирическим данным, дробная часть числа Пи представляет собой нормальную числовую последовательность (хотя доказать это достоверно ещё не удалось), а значит, последовательности цифр из него можно использовать в генерации паролей и просто случайных чисел, или в криптографических алгоритмах (например, в хэшировании). Способов применения можно найти великое множество — надо только включить фантазию.

Больше информации по теме вы можете найти в статье самого Дэвида Бэйли, где он подробно рассказывает про алгоритм и его имплементацию (pdf);

И, похоже, вы только что прочитали первую русскоязычную статью об этом алгоритме в рунете — других я найти не смог.

Как заставить ПК вычислить число пи максимально точно?

Привет ЛОР. Как вычислить точное число Пи? Зачем? Да интересно стало сколько его будет вычислять мой ПК (cpu точнее, расчеты на gpu не берем). В идеале хотелось бы задать много-много знаков, ну хотя бы 20к знаков числа Пи как вычислить? В программировании я ноль.

Линукс тут при том, что вычисления будут вестись в нем, ведь всем известно, что все супер-пупер компьютеры работают на Линуксе.

Его нельзя вычислить максимально точно, оно иррациональное.

Можно, если работать с системой счисления с подходящим основанием — например, с пи-ической.

Выбирай свой любимый язык программирования:

П.С. Гугл знает всё!

В идеале хотелось бы задать много-много знаков, ну хотя бы 20к знаков числа Пи как вычислить?

Прекрати прогуливать уроки. Твой учитель математики вам об этом рассказывал.

ты ноль не только в программировании.

Математику я прогуливал когда она была в школе, мне она не нравилась. А сейчас на заочке на вышмате упомянули про число Пи, вот я и задумался.

karton1 ★★★★★ ( 27.01.18 19:24:39 )
Последнее исправление: karton1 27.01.18 19:25:02 (всего исправлений: 2)

вычисляй сразу pi^e

А чем это круче чем вычисление числа Пи? Я помню что это как то связано с Эйлером.

Забавный факт. При попытке открыть в браузере файл с числом Пи вычисленным с точностью до миллиарда ПК завис. Файрфокс последний, cpu ryzen 1500x. Пишу с xiaomi.

одно трансцендентное иррациональное число в степени другого иррационального трансцендентного числа — это разве не весело?

Мда, выглядит мощно.

Так ты мазохист?

Почему ты так решил?

Математику я прогуливал когда она была в школе, мне она не нравилась. А сейчас на заочке на вышмате

Или я что не понял.

Я вот в школе терпеть не мог только одну вещь — русский язык и литературу. Как вспомню про сочинения, аж в дрожь с тошнотой бросает. Вот бы поступил на филологический 😀

fornlr ★★★★★ ( 27.01.18 19:38:43 )
Последнее исправление: fornlr 27.01.18 19:39:33 (всего исправлений: 1)

Хах, у меня наоборот. Я был самый читающий в школе, меня даже награждали за это, книгу подарили из библиотеки, лол, поэтому русский язык и литература были вообще не проблемой, я их тупо знал, даже не учил. А вот математику я быстро освоить не могу как это требовали на уроке, а дома изучать скучно было, компа и интернета к тому же не было, я просто обкладывался книгами и читал. Фантастику всегда любил, научную, про космос там, будущее.

Это инцест, если учесть, насколько эти два числа тесно связаны.

Продолжаю наблюдение. ПК так и не отвис, черный экран и курсор. Курсор еле-еле шевелится и тормозит при движении. Математика мощная штука ;).

А мог и просто бесконечный цикл с вычислениями степеней рандомной лажи запустить, киловатты утекли бы туда же.