Расчет аннуитетного платежа в excel

history 2 февраля 2015 г.

Расчет кредитов и вкладов
Аннуитет

Рассчитаем в MS EXCEL сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции ПЛТ() , так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.

При кредитовании банки наряду с дифференцированными платежами часто используют аннуитетную схему погашения . Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.

Задача1

Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.

Разбираемся, какая информация содержится в задаче:

Заемщик ежемесячно должен делать платеж банку. Этот платеж включает: сумму в счет погашения части ссуды и сумму для оплаты начисленных за прошедший период процентов на остаток ссуды ;
Сумма ежемесячного платежа (аннуитета) постоянна и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
Сумма для оплаты начисленных за прошедший период процентов уменьшается каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды, увеличивается от месяца к месяцу.
Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
В конце срока задолженность должна быть равна 0 (БС=0).

Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL ПЛТ() .

Примечание . Обзор всех функций аннуитета в статье найдете здесь .

Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.

Примечание : Функция ПЛТ() входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).

Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев). Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет) Пс — Приведенная стоимость всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000. Бс — Будущая стоимость всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0. Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).

Примечание : В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж. В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).

Решение1 Итак, ежемесячный платеж может быть вычислен по формуле =ПЛТ(10%/12; 5*12; 100 000; 0; 0) , результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые банк дал нам, -2107,14 – это деньги, которые мы возвращаем банку .

Альтернативная формула для расчета платежа (общий случай): =-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+ ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)

Если процентная ставка = 0, то формула упростится до =(Пс + Бс)/Кпер Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:

Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А — это аннуитетный платеж (т.е. ПЛТ), К — это коэффициент аннуитета, а S — это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n — количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).

Таблица ежемесячных платежей

Составим таблицу ежемесячных платежей для вышерассмотренной задачи.

Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и ПЛТ() (подробнее см. статью Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга ). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент период , который определяет к какому периоду относится сумма.

Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и ОСПЛТ() (подробнее см. статью Аннуитет. Расчет в MS EXCEL выплаченных процентов за период ).

Примечание . Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию ОБЩПЛАТ() , см. здесь .

Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо ПРПЛТ() или ОСПЛТ() , т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ

Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .

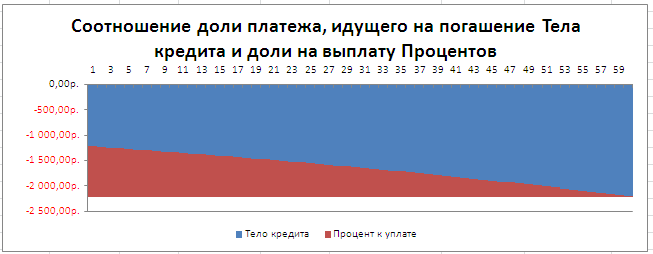
Примечание . В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.

График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P файла примера лист Аннуитет (ПЛТ) , а также на листе Аннуитет (без ПЛТ) . Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см. файл примера лист Аннуитет (ПЛТ), столбцы H:I ).

Задача2

Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.

Решение2 Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0) , результат -6 851,59р. Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.

Расчет аннуитетного платежа в excel

Формула для расчета аннуитетного платежа выглядит следующим образом:

A – сумма кредита;

R – процентная ставка;

N – срок кредита;

Предположим мы хотим взять кредит на 50000 рублей, под 25% годовых на 30 месяцев, подставим известные значения в формулу, чтобы получить сумму месячного аннуитетного платежа, получается:

A = 50000 (сумма кредита)

R = 0.25/12 (месячная процентная ставка)

N = 30 (срок кредита в месяцах)

В результате расчета этой формулы мы получим значение 2258.158, это означает, что тридцать месяцев нам придется выплачивать эту сумму.

Расчет аннуитетного платежа с помощью Excel

Для расчета месячного платежа в Excel есть функция PMT (ПЛТ на русском).

Функция PMT имеет синтаксис: =PMT(rate, nper, pv, [fv],[type])

Аргументы функции PMT(ПЛТ):

rate — процентная ставка;

nper – срок кредита;

pv – сумма кредита;

аргументы [fv] и [type] являются необязательными, [fv] – значение будущей стоимости, аргумент [type] определяет, когда нужно платить он может быть равен 0 – в конце периода (по умолчанию) и 1 – в начале периода.

Возьмем за основу пример выше, подставим значения в эту функцию и сравним результат (перед сумой кредита нужно поставить знак минус, чтобы получить положительное число).

Как видим, значения совпадают, мы можем изменить формат ячейки на числовой и увидеть неокругленную сумму 2258,158162640140

Расчет аннуитетного платежа с помощью SAS

В SAS есть очень гибкая функция mort, с помощью которой можно вычислять не только сумму месячного аннуитетного платежа, но и сумму кредита, ставку и срок.

Функция mort имеет следующий синтаксис: MORT(a,p,r,n).

Аргументы функции mort

a – сумма кредита;

r – процентная ставка;

n – срок кредита;

Наша цель определить сумму месячного аннуитетного платежа, подставим в правильном порядке значения из предыдущего примера в функцию mort, для второго аргумента поставим символ точку «.» получим следующий код:

data mort_example;

payment = mort( 50000 , . , 0.25 / 12 , 30 );

proc print data =mort_example;

run;

После выполнения данного кода увидим результат:

Как было написано выше, с помощью функции mort можно вычислять любые другие неизвестные аргументы, предположим мы знаем сумму месячного платежа, сумму кредита и ставку, требуется вычислить срок, тогда функция вызываться должна так:

term = mort( 50000 , 2258.16 , 0.25 / 12 , .);

Расчет аннуитетного платежа с помощью Oracle PL SQL

В БД Oracle нет встроенной функции для расчета месячного аннуитетного платежа, но её довольно просто написать самому, например вот так:

create or replace function getMortPayment(pAmount in numbe r,
pRate in number ,
pTerm i n number ) return number
is

/*Формула расчета месячного аннуитетного платежа
p := a * r * ((1+r)^n) / ((1+r)^n) -1; */

vPayment number ;

begin

vPayment := pAmount * pRate* power (( 1 +pRate),pTerm)/
( power (( 1 +pRate),pTerm) -1 ) ;

return vPayment;

end ;

select getMortPayment(pAmount => 50000 , pRate => 0.25 / 12 , pTerm => 30 ) as p from dual

Получим результат 2258,15816264014

Как видим, рассчитать месячный аннуитетный платеж совсем не сложно 🙂

Пример функции ПЛТ для расчета аннуитетного платежа в Excel

Функция ПЛТ в Excel используется для расчета фиксированного значения суммы периодических взносов для выплат задолженностей при условии, что процентная ставка является постоянной величиной, и возвращает соответствующее значение.

Примеры использования функции ПЛТ в Excel

С помощью функции ПЛТ можно рассчитать фиксированную сумму ежемесячного платежа по кредиту в банке, если известны тело кредита, значение годовой процентной ставки и число периодов выплат (либо срок действия договора кредитования). Также функция удобна для расчета суммы ежемесячных выплат по депозитам с дополнительными взносами.

Расчет ежемесячного платежа по кредиту в Excel

Пример 1. Определить размер ежемесячного платежа по кредиту с процентной ставкой 23% на сумму 25000 рублей, который должен быть выплачен на протяжении 3 лет.

Вид таблицы данных:

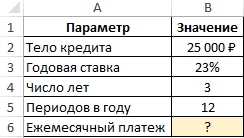
Пример 1.

Для получения искомого значения введем следующую формулу:

ПЛТ.

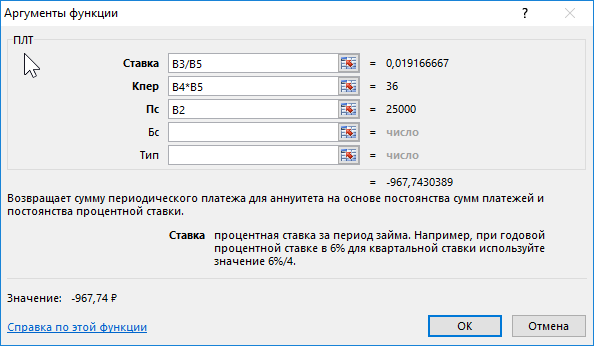
B3/B5 – процентная ставка, приведенная к числу периодов выплат в году;
B4*B5 – число периодов выплат на протяжении действия кредитного договора;
B2 – начальная стоимость кредита (тело кредита).

Результат выполнения формулы:

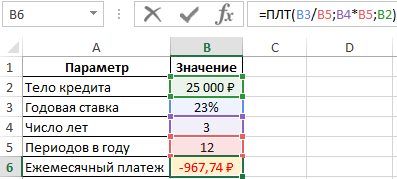
Расчет ежемесячного платежа по кредиту.

Полученное значение является отрицательным числом, поскольку ежемесячные платежи по кредиту являются расходными операциями для заемщика.

Пример расчета суммы переплаты по кредиту в Excel

Пример 2. Определить сумму, которую переплатит заемщик, взявший кредит на сумму 50000 с годовой процентной ставкой 27% и 12 периодами выплат в год. Срок кредитования составляет 5 лет.

Вид таблицы данных:

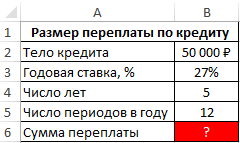
Пример 2.

Для расчета суммы переплат необходимо из общей суммы выплат по кредиту за период действия договора вычесть тело кредита. Для этого используем следующую формулу:

Произведение результата, возвращаемого функцией ПЛТ и количества периодов выплат (B4*B5) соответствует общей сумме выплат за 5 лет. Поскольку функция ПЛТ возвращает отрицательное значение, используем функцию ABS для получения абсолютного значения. В результате вычислений получим:

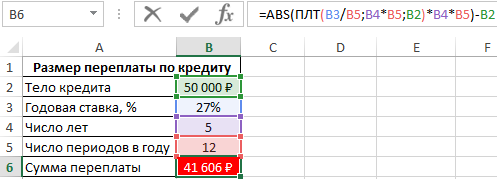
Пример расчета суммы переплаты.

Клиент банка выплатит 50000 рублей тела кредита и еще около 42000 рублей процентов.

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Пример 3. В банке был открыт депозитный счет с начальной суммой 200 000 рублей. Условия договора позволяют выполнять ежемесячное пополнение данного счета. Определить, какую сумму необходимо вносить ежемесячно, чтобы спустя 4 года получить 2000000 рублей. Процентная ставка составляет 11% годовых.

Вид таблицы данных:

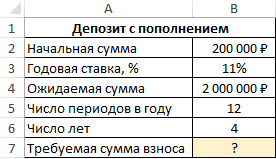
Пример 3.

Искомое значение может быть определено с помощью следующей формулы:

Примечание: для получения корректного результата аргумент пс должен принимать отрицательное значение суммы первоначального взноса.

В результате расчетов получим следующее значение:

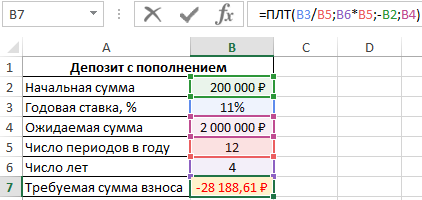
Формула вычисления ежемесячного платежа.

Для накопления 2 млн. рублей клиенту банка потребуется ежемесячно вносить на депозитный счет примерно 28000 рублей.

Особенности использования функции ПЛТ в Excel

Функция имеет следующую синтаксическую запись:

=ПЛТ( ставка; кпер; пс; [бс]; [тип])

ставка – обязательный аргумент, характеризующий числовое значение годовой ставки по задолженности. Может быть указан числовым значением в виде десятичной дроби (например, 0,2 – соответствует 20% годовой ставки) или числом в процентном формате;
кпер – обязательный аргумент, принимающий числовое значение, характеризующее число периодов выплат по задолженности. Может принимать дробные числа, не усекая дробную часть и равномерно распределяя фиксированную сумму платежей между указанным числом периодов;
пс – обязательный аргумент, принимающий числовое значение, которое характеризует начальную стоимость финансового продукта. В случае с выдачей кредита, это значение эквивалентно телу кредита, то есть сумме средств, которую получает заемщик в кредитной организации;
[бс] – необязательный для заполнения аргумент, принимающий числовое значение, которое характеризует оставшуюся сумму задолженности. Например, если этот аргумент явно указан, можно определить, какой должна быть сумма ежемесячного взноса, чтобы при текущей процентной ставке остаток задолженности составил указанную сумму спустя определенное число периодов выплат. Если аргумент явно не указан, он принимается равным 0 (нулю), то есть задолженность будет полностью списана.
[тип] – необязательный для заполнения аргумент, принимающий одно из двух возможных числовых значений:

0 – выплаты производятся в конце периода (если явно не указан, используется по умолчанию).
1 – выплаты в начале периода.

При расчете суммы ежемесячных выплат учитывается только значение годовой процентной ставки. В договорах некоторых финансовых организациях могут быть указаны дополнительные сборы и комиссии, влияющие на итоговый результат.
При указании процентной ставки необходимо выполнять перерасчет в зависимости от количества периодов выплат в году. Платежи могут быть, например, ежемесячными или ежеквартальными. В первом случае аргумент ставка должен быть указан как n%/12, а во втором – n%/4, где n% — годовая процентная ставка.
Аргумент кпер должен быть указан числом, которое получено в результате произведения количества лет, на которые выдан кредит, и количества периодов выплат в году. Например, если ипотечный кредит был выдан на 20 лет, а платежи необходимо делать ежемесячно, аргумент кпер должен быть указан как 20*12 или 240.
Для расчета общей суммы платежей по кредиту можно умножить возвращаемый рассматриваемой функцией результат на количество периодов выплат.

Расчет аннуитетного платежа

Пример расчета аннуитетного платежа (расчеты лучше производить в Microsoft Excel, также можно воспользоваться функцией ПЛТ).

Условие: сумма кредита — 1 000 000 рублей, срок — три года (36 месяцев), ставка — 20%. Погашение осуществляется аннуитетными платежами.

1. Ставка по кредиту в месяц = годовая процентная ставка / 12 месяцев 20%/12 месяцев/100 = 0,0166666666666667

2. Коэффициент аннуитета = (0,0166666666666667*(1+0,0166666666666667)^36/((1+0,0166666666666667)^36—1)=0,0371635833597405

3. Ежемесячный аннуитетный платеж = 0,0371635833597405*1 000 000 рублей = 37 164 рублей

4. Итого переплата по кредиту составила 337 889 рублей

При погашении данного кредита дифференцированными платежами сумма уплаченных процентов по нему составила бы 308 915 рублей

Комментарии 14

Что касается формулы, то в ней опущена половина знаков.
Следует читать как:
1) 20%/12 месяцев/100=0,017, по правилам округления

Ошибка уже в пункте 1, а именно, годовая процентная ставка в 12 % это не то же самое, что 1% в месяц.
Почему так?
Представьте себе, что вы кладёте 1000000 рублей в банк под 12% годовых и банк вам начисляет по 1% каждый месяц:
после 1-го месяца: на вашем счёте 1010000 рублей
после 2-го месяца: на вашем счёте 1020100 рублей
после 3-го месяца: на вашем счёте 1030301 рублей
после 4-го месяца: на вашем счёте 1040604.01 рублей

уже видно, что если бы проценты просто складывались, то после 4-го месяца у вас должно было бы быть 1040000 рублей, вместо этого у вас появились дополнительные 604 рубля 1 копейка. На них тоже капает процент и по итогам года вы получите не 12% годовых, а 12,68 % годовых.

Поэтому, чтоб посчитать процент за месяц, нужно делать так:
процент за год = X
доля за год = X/100
годовой коэфф-т умножения вклада = 1+X/100
месячный коэфф-т умножения вклада = root12(1+X/100)
где root12 это корень 12-ой степени
месячная доля = root12(1+X/100) — 1
месячный процент = (root12(1+X/100)-1)*100

Я, кстати, тоже не поняла. Просто потому, что «выводов» по этим данным может быть «стопятьсот», в зависимости от фантазии и додумок. И формулу сложных процентов смотрела. Хотя тут надо еще посмотреть формулу с дисконтированием денежных потоков — она правильнее отражает ситуацию с «откладыванием».
Например, Евгений может предлагать проценты платить раз в год, но суммы класть на депозит под проценты. И в итоге в конце года немного навариться. Да, так можно, наверное. У банка же много денег, ну дал кому — то 3 ляма, вывел из своего оборота, а мог директору квартиру купить . Но давайте с зарплатой так же поступим — работайте сейчас, а зарплату раз в год. Зато сколько много сразу .
Это лишь один из вариантов.

Нет не понятно. Не понятно зачем откладывать средства на начисленные проценты на депозит не выплачивая их сразу банку.
Да, вы получите на них процент. Сложный. И за год он будет выше чем ставка банка по вкладу.
Но и невыплаченные проценты по кредиту увеличат ваш долг (Точнее не уменьшат его настолько насколько могли бы его уменьшить). На недовыплаченую сумму каждый последующий месяц будут начисляться проценты. Как и на основной долг. По сути, тоже «сложный» процент. Только он будет по гораздо большей ставке — по ставке кредита, а не по ставке депозита. Таким образом выгодой от депозита вы не перекроете начисленные проценты за неоплачиваемую каждый месяц часть долга по кредиту. А наоборот потеряете на разнице процентов между ставками по кредиту и депозиту.
Если чтото не так — поясните подробнее вашу мысль. Желательно с расчетами.

Предприятие решило приобрести в свой офис 3 компьютера стоимостью 8тис.грн. каждый. Банк предлагает кредит на 5 месяцев с последующим ежемесячным погашением равными долями по ставке 25% в год. Рассчитать сумму, которую необходимо возвращать каждый месяц и общую стоимость кредита.

Помогите пожалуйста, уже второй день пытаюсь разобрться как именно это начисляется, формулы все спутались в голове давно, числа никак не хотят сходиться

Katerina314 пишет:
Предприятие решило приобрести в свой офис 3 компьютера стоимостью 8тис.грн. каждый. Банк предлагает кредит на 5 месяцев с последующим ежемесячным погашением равными долями по ставке 25% в год. Рассчитать сумму, которую необходимо возвращать каждый месяц и общую стоимость кредита.

Скорей всего вы уже взяли кредит и погасили его, тем не менее, вероятнее всего, ваш кредитный график выглядел так:

Платеж ОД Проценты Остаток ОД
8 000,00
1 701,37 1 534,71 166,6667 6 465,29
1 701,37 1 566,68 134,6936 4 898,61
1 701,37 1 599,32 102,0544 3 299,29
1 701,37 1 632,64 68,7352 1 666,65
1 701,37 1 666,65 34,7219 —

Короче говоря, ежемесячный платеж — 1701,37. Расчеты приведены при условии, что банк применяет day count convention = 30/360

Формула аннуитетного платежа, расчет платежа

Когда вы берёте в банке кредит, вы обязуетесь в течение определённого срока выплачивать сумму взятого кредита и процентов по нему. Существует несколько способов погашения кредита, распространённый способ — это аннуитетные платежи. В этой статье мы рассмотрим, что такое аннуитетные платежи, узнаем формулу аннуитетного платежа и проведём расчёт.

Аннуитетный и дифференцированный платёж

Аннуитет — это одинаковый по сумме ежемесячный платёж. То есть при аннуитетном платеже вы каждый месяц платите одинаковую сумму (кредит + проценты по нему) независимо от оставшейся суммы задолженности.

Другой способ погашения кредита — это дифференцированный платёж, то есть выплата процентов на оставшуюся задолженность. При дифференцированных платежах ваша сумма ежемесячных выплат будет уменьшаться к концу срока кредита, поскольку вы будете выплачивать проценты за кредит на оставшуюся сумму задолженности. Например, погасив 80% кредита, вы будете платить проценты за оставшуюся сумму (20%).

Для самих банков выгоднее применять аннуитетные платежи, поскольку в этом случае они получают больше прибыли по процентам. Заемщикам же аннуитетные платежи выгоднее в том плане, что удобнее каждый месяц платить одну и ту же сумму, чем каждый раз разную и уточнять, сколько же ему надо внести в следующий месяц.

Формула аннуитетного платежа

В соответствии с формулой аннуитетного платежа размер периодических (ежемесячных) выплат будет составлять:

A = K · S

где А — ежемесячный аннуитетный платёж,
К — коэффициент аннуитета,
S — сумма кредита.

Коэффициент аннуитета рассчитывается по следующей формуле:

где i — месячная процентная ставка по кредиту (= годовая ставка / 12),
n — количество периодов, в течение которых выплачивается кредит.

Поскольку периодичность платежей по кредиту — ежемесячно, то ставка по кредиту (i) берётся месячная. Если процентная ставка 12% годовых, то месячная ставка:
i = 12% / 12 мес = 1%.

С помощью приведённой выше формулы аннуитетного платежа вы можете узнать ежемесячную сумму, которую нужно платить, чтобы погасить кредит.

Расчет аннуитетного платежа

Приведём пример расчета аннуитетного платежа.
Допустим, вы взяли в банке кредит на сумму 30 000 рублей под 18% годовых сроком на 3 года.

Исходные данные:
S = 30 000 рублей
i = 1,5% (18% / 12 мес) = 0,015
n = 36 (3 года х 12 мес)

Подставляем эти значения в формулу и определяем коэффициент аннуитета:

К =	0,015*(1+0,015) 36	= 0,03615
(1+0,015) 36 — 1

Размер ежемесячных выплат:

A = K*S = 0,03615 * 30000 = 1084,57 рублей.

Расчет аннуитетного платежа в Microsoft Excel

Если у вас возникают проблемы с ручным расчётом аннуитетных платежей — можно вычислить в Excel. В Экселе есть специальная функция ПЛТ. Просто создаёте новую таблицу и в любой ячейке вводите строку.

Подставим те же исходные данные, что и в примере, рассмотренном выше. В результате в Экселе нужно ввести следующее выражение:

=ПЛТ(18%/12; 36; -30000)

В скобках формулы указывается по порядку: процентная ставка, количество месяцев, сумма кредита. Можно также записать так:

=ПЛТ(0,015; 36; -30000)

18% годовых / 12 месяцев / 100 = 0,015

В любом случае у нас сумма ежемесячных платежей получится 1084,57 рублей.