конспект урока Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера. Алгоритмы и способы их описания
Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в разработке различных электронных схем. Законы и аппарат алгебры логики стали использоваться при проектировании различных частей компьютеров (память, процессор).
Алгебра логики оперирует с высказываниями. Под высказыванием понимают повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно. Над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания. Наиболее часто используются логические операции, выражаемые словами «не», «и», «или».
Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).
Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера. Алгоритмы и способы их описания.

Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
Логические выражения и логические операции
Общее представление
Логические выражения могут быть простыми и сложными.
Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь».
Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.
В качестве основных логических операций в сложных логических выражениях используются следующие:
— НЕ (логическое отрицание, инверсия);
— ИЛИ (логическое сложение, дизъюнкция);
— И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение — двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например:
— таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции;
— в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции;
— если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.
Операция НЕ — логическое отрицание (инверсия)
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:
— если исходное выражение истинно, то результат его отрицания будет ложным;
— если исходное выражение ложно, то результат его отрицания будет истинным.
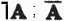
Для операции отрицания НЕ приняты следующие условные обозначения: ; not А. Результат операции отрицания НЕ определяется следующей таблицей истинности:


Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
Приведем примеры отрицания.
1. Высказывание «Земля вращается вокруг Солнца» истинно. Высказывание «Земля не вращается вокруг Солнца» ложно.
2. Высказывание «Пушкин — гениальный русский поэт» истинно. Высказывание «Пушкин — не гениальный русский поэт» ложно.
3. Высказывание «Уравнение у = 4х + 3 в промежутке -2 ≤ х ≤ 2 не имеет корня» ложно. Высказывание «Уравнение у = 4х + 3 в промежутке -2 ≤ х ≤ 2 имеет корень» истинно.
4. Высказывание «4 — простое число» ложно. Высказывание «4 — не простое число» истинно.
5. Принцип работы переключателя настольной лампы таков: если лампа горела, переключатель выключает ее, если лампа не горела — включает ее. Такой переключатель можно считать электрическим аналогом операции отрицания.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение)
Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами.
Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений. Результат операции ИЛИ определяется следующей таблицей истинности:
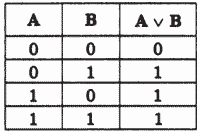
Применяемые обозначения: А или В; A ∨ В; A or В. При выполнении сложных логических преобразований для наглядности условимся пользоваться обозначением А + В, где А, В — аргументы (исходные высказывания). О том, что это логическое сложение, говорят прописные буквы в обозначении высказываний.

Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
Приведем примеры логического сложения.
1. Рассмотрим высказывание «В библиотеке можно взять книгу или встретить знакомого». Это высказывание формально можно представить так: С = A ∨ В, где высказывание А — «В библиотеке можно взять книгу», а В — «В библиотеке можно встретить знакомого». Объединение этих высказываний при помощи операции логического сложения означает, что события могут произойти как отдельно, так и одновременно.
2. Рассмотрим высказывание «Знания или везение — залог сдачи экзаменов». Успешно сдать экзамен может тот, кто все знает, или тот, кому повезло (например, вытянут единственный выученный билет), или тот, кто все знает и при этом выбрал «хороший» билет.
3. Кто хоть однажды использовал елочную гирлянду с параллельным соединением лампочек, знает, что гирлянда будет светить до тех пор, пока цела хотя бы одна лампочка. Логическая операция ИЛИ чрезвычайно схожа с работой подобной гирлянды, ведь результат операции ложь только в одном случае — когда все аргументы ложны.
Операция И — логическое умножение (конъюнкция)
Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение.
Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения. Результат операции И определяется следующей таблицей истинности:
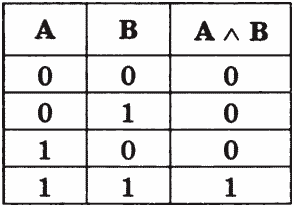
Применяемые обозначения: А и В; А ∧ В; А & В; A and В.
Условимся пользоваться при выполнении сложных логических преобразований обозначением А • В, где А, В — аргументы (исходные высказывания). О том, что это логическое умножение, говорят прописные буквы в обозначении высказываний.

Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
Приведем примеры логического умножения.
1. Рассмотрим высказывание «Учитель должен быть умным и справедливым». Это высказывание формально можно представить так: С = А ∧ В, где высказывание А — «Учитель должен быть умным», а В — «Учитель должен быть справедливым». Объединение этих высказываний при помощи операции логического умножения означает, что учитель должен быть одновременно и умным, и справедливым.
2. Рассмотрим высказывание «Умение и настойчивость приводят к достижению цели». Достижение цели возможно только при одновременной истинности двух предпосылок — умения и настойчивости. выражения. Результат операции И определяется следующей таблицей истинности:
3. Логическую операцию И можно сравнить с последовательным соединением лампочек в гирлянде. При наличии хотя бы одной неработающей лампочки электрическая цепь оказывается разомкнутой, то есть гирлянда не работает. Ток протекает только при одном условии — все составляющие цепи должны быть исправны.

Операция «ЕСЛИ-TO» — логическое следование (импликация)
Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
если А, то В; А влечет В; if A then В; А —> В.
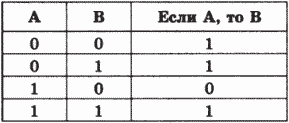

Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствии) ложно.
Приведем примеры операции следования.
1. Рассмотрим высказывание «Если идет дождь, то на улице сыро». Здесь исходные высказывания «Идет дождь» и «На улице сыро». Если не идет дождь и не сыро на улице, результат операции следования — истина. На улице может быть сыро и без дождя, например, когда прошла поливочная маши¬на или дождь прошел накануне. Результат операции ложен только тогда, когда дождь идет, а на улице не сыро.
2. Рассмотрим два высказывания: А , В . Операция А —> В означает следующее: «Если число делится на 9, то оно делится и на 3». Рассмотрим возможные варианты:

Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Применяемое обозначение: А ~ В.
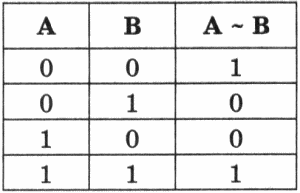

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
Приведем примеры операции эквивалентности.
1. «День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом»;
2. «Добиться результата в спорте можно тогда и только тогда, когда приложено максимум усилий».
Лекция: Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера. Алгоритмы и способы их описания.
Для описания того, как функционируют аппаратные средства компьютера очень удобен математический аппарат алгебры логики, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: «1» и «0».
Из этого следует, что одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных.
Логика – это наука о формах и способах мышления.
Основы формальной логики заложил древнегреческий мыслитель Аристотель.
Логические переменные в алгебре логики обозначаются прописными латинскими буквами, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0).
Логическое умножение (конъюнкция) «И» AÙB
AÙBистинно тогда и только тогда, когда оба высказывания Aи B истинны.
Логическое сложение (дизъюнкция) «ИЛИ» AÚB
AÚBложно тогда и только тогда, когда оба высказывания A и Bложны.
Логическое отрицание (инверсия) «НЕ» ØA,( )
Логическое отрицание (инверсия) делает истинное выражение ложным и, наоборот, ложное – истинным.
Таблица истинности для основных логических функций
| A | B | AÙB конъюнкция | AÚB дизъюнкция | ØA инверсия |
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Логический элемент – простейшая структурная единица ЭВМ – выполняющая определенную логическую операцию над двоичными переменными согласно правилам алгебры логики.
Реализуется обычно на электронных приборах (полупроводниковых диодах, транзисторах) и резисторах, либо в виде интегральной микросхемы; имеет несколько входов для приема сигналов, соответствующих исходным переменным, и выход для выдачи сигнала, соответствующего результату операций. Для логических элементов приняты дискретные значения входных и выходных сигналов («0» и «1»).
Базовые логические элементы ЭВМ реализуют три основные логические операции:
конъюнктор – логический элемент «И» логическое умножение;
дизъюнктор – логический элемент «ИЛИ» логическое сложение;
инвертор – логический элемент «НЕ» инверсию.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала 1, нет импульса – . На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов.
информатика
ИНФОРМАТИКА- НАУКА, ИЗУЧАЮЩАЯ СПОСОБЫ АВТОМАТИЗИРОВАННОГО СОЗДАНИЯ, ХРАНЕНИЯ, ОБРАБОТКИ, ИСПОЛЬЗОВАНИЯ, ПЕРЕДАЧИ И ЗАЩИТЫ ИНФОРМАЦИИ.
ИНФОРМАЦИЯ – ЭТО НАБОР СИМВОЛОВ, ГРАФИЧЕСКИХ ОБРАЗОВ ИЛИ ЗВУКОВЫХ СИГНАЛОВ, НЕСУЩИХ ОПРЕДЕЛЕННУЮ СМЫСЛОВУЮ НАГРУЗКУ.
Например, этот или любой другой текст, имеющий определенный смысл, состоит из набора символов- букв, знаков препинания, цифр, которые объединяются в слова, те в свою очередь — в предложения и далее- в абзацы. Человек, чтобы сообщить что-либо собеседнику произносит определенные фразы- то есть издает звуковые сигналы. Данные – это зарегистрированные сигналы. Однако, не все данные являются информацией. Слыша речь на незнакомом языке, мы получаем данные, но не получаем информацию, в связи с тем, что не владеем методом преобразования данных в известные нам понятия. Изображение на знаке дорожного движения доводит до водителя автомобиля определенную информацию, а для человека, не понимающего эти знаки, они не являются информацией.
Итак, информация – это продукт преобразования зарегистрированных сигналов в известные субъекту понятия. Огромное влияние в передаче информации сыграла письменность. Затем — телефон, радио. Сейчас – телевидение и компьютерные технологии.
ЭЛЕКТРОННО-ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЭВМ) ИЛИ КОМПЬЮТЕР (англ. computer- -вычислитель)-УСТРОЙСТВО ДЛЯ АВТОМАТИЗИРОВАННОЙ ОБРАБОТКИ ИНФОРМАЦИИ. Принципиальное отличие использования ЭВМ от всех других способов обработки информации заключается в способности выполнения определенных операций без непосредственного участия человека, но по заранее составленной им программе. Информация в современном мире приравнивается по своему значению для развития общества или страны к важнейшим ресурсам наряду с сырьем и энергией. Еще в 1971 году президент Академии наук США Ф.Хандлер говорил: «Наша экономика основана не на естественных ресурсах, а на умах и применении научного знания».
В развитых странах большинство работающих заняты не в сфере производства, а в той или иной степени занимаются обработкой информации. Поэтому философы называют нашу эпоху постиндустриальной. В 1983 году американский сенатор Г.Харт охарактеризовал этот процесс так: «Мы переходим от экономики, основанной на тяжелой промышленности, к экономике, которая все больше ориентируется на информацию, новейшую технику и технологию, средства связи и услуги..»
2. КРАТКАЯ ИСТОРИЯ РАЗВИТИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ.
Вся история развития человеческого общества связана с накоплением и обменом информацией (наскальная живопись, письменность, библиотеки, почта, телефон, радио, счеты и механические арифмометры и др.). Коренной перелом в области технологии обработки информации начался после второй мировой войны.
В вычислительных машинах первого поколения основными элементами были электронные лампы. Эти машины занимали громадные залы, весили сотни тонн и расходовали сотни киловатт электроэнергии. Их быстродействие и надежность были низкими, а стоимость достигала 500-700 тысяч долларов.
Появление более мощных и дешевых ЭВМ второго поколения стало возможным благодаря изобретению в 1948 году полупроводниковых устройств- транзисторов. Главный недостаток машин первого и второго поколений заключался в том, что они собирались из большого числа компонент, соединяемых между собой. Точки соединения (пайки) являются самыми ненадежными местами в электронной технике, поэтому эти ЭВМ часто выходили из строя.
В ЭВМ третьего поколения (с середины 60-х годов ХХ века) стали использоваться интегральные микросхемы (чипы)- устройства, содержащие в себе тысячи транзисторов и других элементов, но изготовляемые как единое целое, без сварных или паяных соединений этих элементов между собой. Это привело не только к резкому увеличению надежности ЭВМ, но и к снижению размеров, энергопотребления и стоимости (до 50 тысяч долларов).
История ЭВМ четвертого поколения началась в 1970 году, когда ранее никому не известная американская фирма INTEL создала большую интегральную схему (БИС), содержащую в себе практически всю основную электронику компьютера. Цена одной такой схемы (микропроцессора) составляла всего несколько десятков долларов, что в итоге и привело к снижению цен на ЭВМ до уровня доступных широкому кругу пользователей.
СОВРЕМЕННЫЕ КОМПЬТЕРЫ- ЭТО ЭВМ ЧЕТВЕРТОГО ПОКОЛЕНИЯ, В КОТОРЫХ ИСПОЛЬЗУЮТСЯ БОЛЬШИЕ ИНТЕГРАЛЬНЫЕ СХЕМЫ.
90-ые годы ХХ-го века ознаменовались бурным развитием компьютерных сетей, охватывающих весь мир. Именно к началу 90-ых количество подключенных к ним компьютеров достигло такого большого значения, что объем ресурсов доступных пользователям сетей привел к переходу ЭВМ в новое качество. Компьютеры стали инструментом для принципиально нового способа общения людей через сети, обеспечивающего практически неограниченный доступ к информации, находящейся на огромном множестве компьюторов во всем мире — «глобальной информационной среде обитания».
6.ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ И ЕЕ ОБЪЕМ.
ЛЮБОЕ СООБЩЕНИЕ НА ЛЮБОМ ЯЗЫКЕ СОСТОИТ ИЗ ПОСЛЕДОВАТЕЛЬНОСТИ СИМВОЛОВ- БУКВ, ЦИФР, ЗНАКОВ. Действительно, в каждом языке есть свой алфавит из определенного набора букв (например, в русском- 33 буквы, английском- 26, и т.д.). Из этих букв образуются слова, которые в свою очередь, вместе с цифрами и знаками препинания образуют предложения, в результате чего и создается текстовое сообщение. Не является исключением и язык на котором «говорит» компьютер, только набор букв в этом языке является минимально возможным.
В КОМПЬЮТЕРЕ ИСПОЛЬЗУЮТСЯ 2 СИМВОЛА- НОЛЬ И ЕДИНИЦА (0 и 1), АНАЛОГИЧНО ТОМУ, КАК В АЗБУКЕ МОРЗЕ ИСПОЛЬЗУЮТСЯ ТОЧКА И ТИРЕ. Действительно, закодировав привычные человеку символы (буквы, цифры, знаки) в виде нулей и единиц (или точек и тире), можно составить, передать и сохранить любое сообщение.
ЭТО СВЯЗАНО С ТЕМ, ЧТО ИНФОРМАЦИЮ, ПРЕДСТАВЛЕННУЮ В ТАКОМ ВИДЕ, ЛЕГКО ТЕХНИЧЕСКИ СМОДЕЛИРОВАТЬ, НАПРИМЕР, В ВИДЕ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ. Если в какой-то момент времени по проводнику идет ток, то по нему передается единица, если тока нет- ноль. Аналогично, если направление магнитного поля на каком-то участке поверхности магнитного диска одно- на этом участке записан ноль, другое- единица. Если определенный участок поверхности оптического диска отражает лазерный луч- на нем записан ноль, не отражает- единица.
ОБЪЕМ ИНФОРМАЦИИ, НЕОБХОДИМЫЙ ДЛЯ ЗАПОМИНАНИЯ ОДНОГО ИЗ ДВУХ СИМВОЛОВ-0 ИЛИ 1, НАЗЫВАЕТСЯ 1 БИТ (англ. binary digit- двоичная единица). 1 бит- минимально возможный объем информации. Он соответствует промежутку времени, в течение которого по проводнику передается или не передается электрический сигнал, участку поверхности магнитного диска, частицы которого намагничены в том или другом направлении, участку поверхности оптического диска, который отражает или не отражает лазерный луч, одному триггеру, находящемуся в одном из двух возможных состояний.
Итак, если у нас есть один бит, то с его помощью мы можем закодировать один из двух символов- либо 0, либо 1.
Если же есть 2 бита, то из них можно составить один из четырех вариантов кодов: 00 , 01 , 10 , 11 .
Если есть 3 бита- один из восьми: 000 , 001 , 010 , 100 , 110 , 101 , 011 , 111 .
1 бит- 2 варианта,
2 бита- 4 варианта,
3 бита- 8 вариантов;
Продолжая дальше, получим:
4 бита- 16 вариантов,
5 бит- 32 варианта,
6 бит- 64 варианта,
7 бит- 128 вариантов,
8 бит- 256 вариантов,
9 бит- 512 вариантов,
10 бит- 1024 варианта,
N бит — 2 в степени N вариантов.
В обычной жизни нам достаточно 150-160 стандартных символов (больших и маленьких русских и латинских букв, цифр, знаков препинания, арифметических действий и т.п.). Если каждому из них будет соответствовать свой код из нулей и единиц, то 7 бит для этого будет недостаточно (7 бит позволят закодировать только 128 различных символов), поэтому используют 8 бит.
ДЛЯ КОДИРОВАНИЯ ОДНОГО ПРИВЫЧНОГО ЧЕЛОВЕКУ СИМВОЛА В КОМПЬЮТЕРЕ ИСПОЛЬЗУЕТСЯ 8 БИТ, ЧТО ПОЗВОЛЯЕТ ЗАКОДИРОВАТЬ 256 РАЗЛИЧНЫХ СИМВОЛОВ.
СТАНДАРТНЫЙ НАБОР ИЗ 256 СИМВОЛОВ НАЗЫВАЕТСЯ ASCII ( произносится «аски», означает «Американский Стандартный Код для Обмена Информацией»- англ. American Standart Code for Information Interchange).
ОН ВКЛЮЧАЕТ В СЕБЯ БОЛЬШИЕ И МАЛЕНЬКИЕ РУССКИЕ И ЛАТИНСКИЕ БУКВЫ, ЦИФРЫ, ЗНАКИ ПРЕПИНАНИЯ И АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ И Т.П.
КАЖДОМУ СИМВОЛУ ASCII СООТВЕТСТВУЕТ 8-БИТОВЫЙ ДВОИЧНЫЙ КОД, НАПРИМЕР:
A — 01000001, B — 01000010, C — 01000011, D — 01000100, и т.д.
Таким образом, если человек создает текстовый файл и записывает его на диск, то на самом деле каждый введенный человеком символ хранится в памяти компьютера в виде набора из восьми нулей и единиц. При выводе этого текста на экран или на бумагу специальные схемы — знакогенераторы видеоадаптера (устройства, управляющего работой дисплея) или принтера образуют в соответствии с этими кодами изображения соответствующих символов.
Набор ASCII был разработан в США Американским Национальным Институтом Стандартов (ANSI), но может быть использован и в других странах, поскольку вторая половина из 256 стандартных символов, т.е. 128 символов, могут быть с помощью специальных программ заменены на другие, в частности на символы национального алфавита, в нашем случае — буквы кириллицы. Поэтому, например, передавать по электронной почте за границу тексты, содержащие русские буквы, бессмысленно. В англоязычных странах на экране дисплея вместо русской буквы Ь будет высвечиваться символ английского фунта стерлинга, вместо буквы р — греческая буква альфа, вместо буквы л — одна вторая и т.д.
ОБЪЕМ ИНФОРМАЦИИ, НЕОБХОДИМЫЙ ДЛЯ ЗАПОМИНАНИЯ ОДНОГО СИМВОЛА ASCII НАЗЫВАЕТСЯ 1 БАЙТ.
Очевидно что, поскольку под один стандартный ASCII-символ отводится 8 бит,
Остальные единицы объема информации являются производными от байта:
1 КИЛОБАЙТ = 1024 БАЙТА И СООТВЕТСТВУЕТ ПРИМЕРНО ПОЛОВИНЕ СТРАНИЦЫ ТЕКСТА,
1 МЕГАБАЙТ = 1024 КИЛОБАЙТАМ И СООТВЕТСТВУЕТ ПРИМЕРНО 500 СТРАНИЦАМ ТЕКСТА,
1 ГИГАБАЙТ = 1024 МЕГАБАЙТАМ И СООТВЕТСТВУЕТ ПРИМЕРНО 2 КОМПЛЕКТАМ ЭНЦИКЛОПЕДИИ,
1 ТЕРАБАЙТ = 1024 ГИГАБАЙТАМ И СООТВЕТСТВУЕТ ПРИМЕРНО 2000 КОМПЛЕКТАМ ЭНЦИКЛОПЕДИИ.
Обратите внимание, что в информатике смысл приставок кило- , мега- и других в общепринятом смысле выполняется не точно, а приближенно, поскольку соответствует увеличению не в 1000, а в 1024 раза.
СКОРОСТЬ ПЕРЕДАЧИ ИНФОРМАЦИИ ПО ЛИНИЯМ СВЯЗИ ИЗМЕРЯЕТСЯ В БОДАХ.
1 БОД = 1 БИТ/СЕК.
В частности, если говорят, что пропускная способность какого-то устройства составляет 28 Килобод, то это значит, что с его помощью можно передать по линии связи около 28 тысяч нулей и единиц за одну секунду.
7. СЖАТИЕ ИНФОРМАЦИИ НА ДИСКЕ
ИНФОРМАЦИЮ НА ДИСКЕ МОЖНО ОБРАБОТАТЬ С ПОМОЩЬЮ СПЕЦИАЛЬНЫХ ПРОГРАММ ТАКИМ ОБРАЗОМ, ЧТОБЫ ОНА ЗАНИМАЛА МЕНЬШИЙ ОБЪЕМ.
Существуют различные методы сжатия информации. Некоторые из них ориентированы на сжатие текстовых файлов, другие — графических, и т.д. Однако во всех них используется общая идея, заключающаяся в замене повторяющихся последовательностей бит более короткими кодами. Например, в романе Л.Н.Толстого «Война и мир» несколько миллионов слов, но большинство из них повторяется не один раз, а некоторые- до нескольких тысяч раз. Если все слова пронумеровать, текст можно хранить в виде последовательности чисел — по одному на слово, причем если повторяются слова, то повторяются и числа. Поэтому, такой текст (особенно очень большой, поскольку в нем чаще будут повторяться одни и те же слова) будет занимать меньше места.
Сжатие информации используют, если объем носителя информации недостаточен для хранения требуемого объема информации или информацию надо послать по электронной почте
Программы, используемые при сжатии отдельных файлов называются архиваторами. Эти программы часто позволяют достичь степени сжатия информации в несколько раз.