Представление целых и вещественных чисел в компьютере

Тест по информатике Представление чисел в компьютере для 8 класса

Тест по информатике Представление чисел в компьютере для 8 класса с ответами. В тесте 2 варианта, каждый включает в себя 7 заданий.

1. Если число положительное, то в знаковый разряд помещается

2. Числом в нормальной форме с нормализованной мантиссой (правильной дробью, имеющей после запятой цифру, отличную от нуля) является:

1) 0,341 x 10 9
2) 1997
3) 213,5629
4) 0,002311

3. Беззнаковым 8-разрядным представлением числа 63₁₀ является

1) 11111100
2) 111111
3) 00000101
4) 00111111

4. Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?

5. При записи числа в форме A = ± m x q p , где m — это

1) порядок числа
2) основание системы счисления
3) мантисса
4) само вещественное число

6. Укажите десятичный эквивалент числа, прямой код которого 01001100 записан в 8-разрядном формате со знаком

1) 66
2) 76
3) -76
4) верного ответа в предложенных вариантах нет

7. Укажите число, записанное в естественной форме

1) 0,38005611 x 10 2
2) 1,257824E+5
3) 0,01357
4) нет числа, записанного в естественной форме

Алгоритм представления вещественного числа в памяти компьютера

Перевести число из Р-ичной системы в двоичную
Представить двоичное число в нормализованной экспоненциальной форме
Рассчитать смещённый порядок числа
Разместить знак, порядок и мантиссу в соответствующие разряды

На этом, пожалуй, остановимся. Получилось, что число 0,14 в двоичной записи приблизительно равно

Объясните задачу про представление вещественных чисел в памяти компьютера

Собственно знать как и что представляется в компе — необходимо, а особенно как представляются вещественные числа.

Как я рассуждаю:
1). в задачи речь идёт о типе float(вещественный, да и с 4-мя байтами. Это однозначно он)
2). я понял как вычислили число 127, но я понять не могу, почему именно 2 127 (почему именно 2, а не 10?)
3). Вот тут у меня вообще тёмный лес: 2 23 – 1 ≈ 2 23 = 2 (102,3) ≈ 1000 2,3 = 10 (32,3) ≈ 107. (тут возможны ошибки, на скрине всё нормально написано).

Будьте добры объяснить новечку что и как/откуда тут берётся, буду крайне благодарен.

Скрин задачи прилагаю (там где не понятно выделил).

Представление вещественных чисел в памяти ЭВМ
Помогите разобраться как представляются вещественные числа в памяти ЭВМ написал прогу masm .

Записать представление вещественных чисел в памяти ЭВМ на основе стандарта IEEE 754
Здравствуйте! Помогите пожалуйста с лабораторной работой, очень срочно

Внутреннее представление чисел в памяти компьютера. Проверить правильность решения
Не понимаю формулировку задания:в формат числа со знаком и числа без знака (использовать формат.

Представление графа в памяти компьютера
Составьте программу, которая содержит функцию (или процедуру) создания заданного способа.

в памяти все хранится в двоичной системе, поэтому логично, что 2, а не 10
порядок — это степень, в которое возводится основание системы счисления. основание 2. поэтому 2^127
теперь по поводу мантиссы. там 24 бита. 1 бит это знак. остается 23 бита. сколько разных чисел можно получить с их помощью? 2^23. очевидно, одно из чисел будет нулем. следовательно, наибольшее число 2^23 — 1. минус единицей можно пренебречь для упрощения дальнейших расчетов.
далее 23=10*2.3
возведем 2 в степень 10. получим 1024. это примерно равно 1000. пишем 1000 для упрощения.
очевидно 1000=10^3
получаем 10^(3*2.3) = 10^(6.9)
округляем степень до 7

Примеры

Проведем нормализацию: –1,111101101₂ × 2 6

СП = 127 + 6 = 133 = 10000101₂

Вещественные числа в памяти компьютера

Вещественные числа в памяти компьютера представляются в форме с плавающей точкой.

Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:

R = m * (р^n) Например, число 25,324 можно записать в таком виде: 0.25324х102. Здесь m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».

Однако справедливы и следующие равенства:

25,324 = 2,5324*(10^1) = 0,0025324*(10^4) = 0,25324*(10^2) и т.п. Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализован-ном представлении должна удовлетворять условию:

± машинный порядок М А Н Т И С С А

В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы.

Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:

Машинный порядок 0 1 2 3 . 64 65 . 125 126 127 Математический порядок -64 -63 -62 -61 . 0 1 . 61 62 63 Если обозначить машинный порядок Мр, а математический — р, то связь между ними ыразится такой формулой:

Мр = р + 64. Итак, машинный порядок смещен относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает.

Полученная формула записана в десятичной системе. Поскольку 6410=4016 (проверьте!), то в шестнадцатеричной системе формула примет вид:

Мр16 = р16 + 4016 И, наконец, в двоичной системе:

Мр2 = р2+100 00002 Теперь мы можем записать внутреннее представление числа 25,324 в форме с плавающей точкой. Переведем его в двоичную систему счисления с 24 значащими цифрами. 25,32410= 11001,01010010111100011012 Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,110010101001011110001101*10101 Здесь мантисса, основание системы счисления (210=102) и порядок (510=1012)записаны в двоичной системе. Вычислим машинный порядок. Мр2 = 101 + 100 0000 = 100 0101 Запишем представление числа в ячейке памяти. 01000101 11001010 10010111 10001101 Это и есть искомый результат. Его можно переписать в более компактной шестнадцатеричной форме:

45 CA 97 8D Для того, чтобы получить внутреннее представление отрицательного числа -25,324,достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.

11000101 11001010 10010111 10001101 А в шестнадцатеричной форме:

C5 CA 97 8D Никакого инвертирования, как для отрицательных чисел с фиксированной точкой, здесь не происходит.

Рассмотрим, наконец, вопрос о диапазоне чисел, представимых в форме с плавающей точкой. Очевидно, положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим порядком:

0,111111111111111111111111*1021111111 Если перевести в десятичную систему, то получится

Rmax = (1 — 2-24) * 264 = 1019 Очевидно, что диапазон вещественных чисел значительно шире диапазона целых чисел. Если в результате вычислений получается число по модулю большее, чем Rmax, то происходит прерывание работы процессора. Такая ситуация называется переполнением при вычислениях с плавающей точкой. Наименьшее по модулю ненулевое значение равно:

(1/2) * 2-64=2-66. Любые значения, меньшие данного по абсолютной величине, воспринимаются процессором как нулевые.

Как известно из математики, множество действительных чисел бесконечно и непрерывно. Множество же вещественных чисел, представимых в памяти ЭВМ в форме с плавающей точкой, является ограниченным и дискретным. Каждое следующее значение получается прибавлением к мантиссе предыдущего единицы в последнем (24-м) разряде. Количество вещественных чисел, точно представимых в па-мяти машины, вычисляется по формуле:

N = 2t * ( U — L+ 1) + 1. Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, L = -64) получается:

N = 2 146 683 548. Все же остальные числа, не попадающие в это множество, но находящиеся в диапазоне допустимых значений, представляются в памяти приближенно (мантисса обрезается на 24-м разряде). А поскольку числа имеют погрешности, то и результаты вычислений с этими числами также будут содержать погрешность. Из сказанного следует вывод: вычисления с вещественными числами в компьютере выполняются приближенно.

Представление вещественных чисел в компьютере

Система вещественных чисел в математических вычислениях предполагается непрерывной и бесконечной, т.е. не имеющей ограничений на диапазон и точность представления чисел. Однако в компьютерах числа хранятся в регистрах и ячейках памяти с ограниченным количеством разрядов. В следствие этого система вещественных чисел, представимых в машине, является дискретной (прерывной) и конечной.

При написании вещественных чисел в программах вместо привычной запятой принято ставить точку. Для отображения вещественных чисел, которые могут быть как очень маленькими, так и очень большими, используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1.25 в этой форме можно представить так:

1.25 . 10 0 = 0.125 . 10 1 = 0.0125 . 10 2 = .

12.5 . 10 -1 = 125.0 . 10 -2 = 1250.0 . 10 -3 = . .

Любое число N в системе счисления с основанием q можно записать в виде N = M . q p , где M — множитель, содержащий все цифры числа (мантисса), а p — целое число, называемое порядком. Такой способ записи чисел называется представлением числа с плавающей точкой.

Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует:

Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля: 0.1₂ M| < 1. Если это требование выполнено, то число называется нормализованным

Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q, а само основание — в десятичной системе. Примеры нормализованного представления:

Десятичная система	Двоичная система
753.15 = 0.75315 . 10 3 ;	– 101.01 = – 0.10101 . 2 11 (порядок 11₂ = 3₁₀)
– 0.000034 = – 0.34 . 10 -4 ;	0.000011 = 0.11 . 2 -100 (порядок —100₂ = —4₁₀).

Вещественные числа в компьютерах различных типов записываются по-разному, тем не менее, все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру следующего вида:

Здесь порядок n-разрядного нормализованного числа задается в так называемой смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2 k-1 — 1). Например, порядок, принимающий значения в диапазоне от —128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255.

Использование смещенной формы позволяет производить операции над порядками, как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.

Стандартные форматы представления вещественных чисел:

1) одинарный – 32-разрядное нормализованное число со знаком, 8-разрядным смещенным порядком и 24-разрядной мантиссой (старший бит мантиссы, всегда равный 1, не хранится в памяти, и размер поля, выделенного для хранения мантиссы, составляет только 23 разряда).

2) двойной – 64-разрядное нормализованное число со знаком, 11-разрядным смещенным порядком и 53-разрядной мантиссой (старший бит мантиссы не хранится, размер поля, выделенного для хранения мантиссы, составляет 52 разряда).

3) расширенный – 80-разрядное число со знаком, 15-разрядным смещенным порядком и 64-разрядной мантиссой. Позволяет хранить ненормализованные числа.

Следует отметить, что вещественный формат с m-разрядной мантиссой позволяет абсолютно точно представлять m-разрядные целые числа, т. е. любое двоичное целое число, содержащее не более m разрядов, может быть без искажений преобразовано в вещественный формат.

Выполнение арифметических действий
над нормализованными числами

К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.

Сложение и вычитание

При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.

В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

Пример 1. Сложить двоичные нормализованные числа 0.10111 . 2 -1 и 0.11011 . 2 10 . Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:

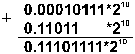
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101 . 2 10 и 0.11101 . 2 1 . Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:

Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы:
0.1101 . 2 0 .

Умножение

При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.

Пример 3. Выполнить умножение двоичных нормализованных чисел:

(0.11101 . 2 101 ) . (0.1001 . 2 11 ) = (0.11101 . 0.1001) . 2 (101+11) = 0.100000101 . 2 1000 .

Деление

При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.

Пример 4. Выполнить деление двоичных нормализованных чисел:

0.1111 . 2 100 : 0.101 . 2 11 = (0.1111 : 0.101) . 2 (100-11) = 1.1 . 2 1 = 0.11 . 2 10 .

Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

© cyberpedia.su 2017-2020 — Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!

Представление вещественных чисел в памяти компьютера