блог админа
♦ представление целых чисел;
♦ размер ячейки и диапазон значений чисел;
♦ особенности работы компьютер с целыми числами;
♦ представление вещественных чисел;
♦ особенности работы компьютера с вещественными числами.
Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном счете сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1. Поэтому современные компьютерные технологииназывают цифровыми технологиями.
В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.
Представление целых чисел
Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальная ячейка, в которой может храниться целое число, имеет размер 8 битов — 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете. Результат перевода:
Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так:
Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.
Самый старший разряд — первый слева, хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:
Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 2 7 = 128. Значит:
011111112 = 128 — 1 = 127.
Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.
Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25? Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. К сожалению, в компьютере все несколько сложнее.
Для представления отрицательных целых чисел используется дополнительный код.
Получить дополнительный код можно по следующему алгоритму:
1) записать внутреннее представление положительного числа X;
2) записать обратный код этого числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.
Определим по этим правилам внутреннее представление числа -2510 в 8-разрядной ячейке:
1) 00011001
2) 11100110
3) +1
11100111 — это и есть представление числа -25.
В результате выполнения такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.
Проверим полученный результат. Очевидно, что при сложении чисел +25 и -25 должен получиться ноль.
00011001
+11100111
1 00000000
Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается ноль!
Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.
Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 2 6 .
Размер ячейки к диапазон значений чисел
Наибольшее по модулю отрицательное значение в 8-разрядной ячейке равно -2 7 = -128. Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий:
Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим:
Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки:
Диапазон для 32-разрядной ячейки получается достаточно большим:
Особенности работы компьютера с целыми числами
Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности диапазона допустимых значений. Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.
Представление вещественных чисел
Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с вещественными числами.
Всякое вещественное число (X) можно записать в виде произведения мантиссы m и основания системы счисления р в некоторой целой степени n, которую называют порядком:
Например, число 25,324 можно записать в таком виде: 0,25324 · 10 2 . Здесь m = 0,25324 — мантисса, n = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел. Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.
Особенности работы компьютера с вещественными числами
1. Диапазон вещественных чисел ограничен. Но он значительно шире, чем для рассмотренного ранее способа представления целых чисел. Например, при использовании 32-разрядной ячейки этот диапазон следующий:
2. Выход за диапазон (переполнение) — аварийная ситуация для процессора, который прерывает свою работу.
3. Результаты машинных вычислений с вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшается.
Коротко о главном
В памяти компьютера целые числа представляются в двоичной системе счисления и могут занимать ячейку размером 8, 16, 32 и т. д. битов.
Диапазон значений целых чисел ограничен. Чем больше размер ячейки, тем шире диапазон.
При выходе результатов вычислений с целыми числами за допустимый диапазон работа процессора не прерывается. При этом результаты могут оказаться неверными.
Вещественные числа представляются в виде совокупности мантиссы и порядка в двоичной системе счисления. Обычный размер ячейки — 32 или 64 бита.
Результаты вычислений с вещественными числами приближенные. Переполнение приводит к прерыванию работы процессора.
Вопросы и задания
1. Как в памяти компьютера представляются целые положительные и отрицательные числа?
2. Укажите, каков был бы диапазон значений целых чисел, если бы для их хранения использовалась 4-разрядная ячейка.
3. Запишите внутреннее представление следующих десятичных чисел, используя 8-разрядную ячейку.
а) 32; б) -32; в) 102; г) -102; д) 126; е) -126.
4. Определите, каким десятичным числам соответствуют следующие двоичные коды 8-разрядного представления целых чисел.
а) 00010101; б) 11111110; в) 00111111; г) 10101010.
Представление числовых данных в памяти ЭВМ
Цель работы: ознакомить студентов с представлением чисел в компьютере.
Теоретические сведения
Представление целых чисел
В компьютере все числа представляются в двоичном виде, то есть в виде комбинаций нулей и единиц. Для представления каждого числа выделяется определенное количество битов. Поэтому в компьютере можно представить не любое число, а только числа из определенного диапазона.
Если для представления числа в компьютере выделить 2 бита, то можно представить всего четыре разных числа: 00, 01, 10 и 11. Если для представления числа выделить 3 бита, то можно представить 8 разных чисел: 000, 001, 010, 011, 100, 101, 110, 111. Если же для представления числа выделить N битов, то можно представить 2 n разных чисел.
Пусть для представления числа используется 1 байт (8 битов). Тогда можно представить: 2 8 =256 разных чисел: от 0000 0000 до 1111 1111.Если перевести эти числа в десятичную систему, получится: 000000002=010, 111111112=25510. Значит при использовании для представления числа 1 байта можно представить числа от 0 до 255.
Для того чтобы в компьютере можно было представить как положительные, так и отрицательные числа, используются следующие правила:
1. Самый старший (левый) бит числа является знаковым. Если этот бит равен 0, число положительное. Если же он равен 1, число отрицательное.
2. Числа хранятся в дополнительном коде.
Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число.
Например, если число 37(10) = 100101(2) объявлено величиной типа Integer (шестнадцатибитовое со знаком), то его прямым кодом будет 0000000000100101, а если величиной типа LongInt (тридцатидвухбитовое со знаком), то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричное представление кода. Полученные коды можно переписать соответственно как 0025(16) и 00000025(16).
Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
1. Записать прямой код модуля числа;
2. Инвертировать его (заменить единицы нулями, нули – единицами);
3. Прибавить к инверсному коду единицу.
При получении числа по его дополнительному коду прежде всего необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:
1. Вычесть из кода числа 1;
2. Инвертировать код;
3. Перевести в десятичную систему счисления. Полученное число записать со знаком минус.
Практические примеры
Для примеров с 1 – 7 предполагаем, что для представления числа в памяти компьютера используются 1 байт (8 битов).
Пример 1
Определить, является ли число 101101 положительным или отрицательным
1)Допишем слева недостающие нули, так чтобы в представлении числа было ровно 8 битов:00101101
2)Самый левый бит равен 0, значит число положительное: 00101101
Ответ: число 101101 – число положительное.
Пример 2
Определить, является число 10111011 положительным или отрицательным.
1) Допишем слева недостающие нули так, чтобы число было 8 битов. Здесь число уже содержит 8 цифр, поэтому нули добавлять не надо: 10111011
2) Самый левый бит равен 1, значит число отрицательное: 10111011
Ответ: 10111011 – число отрицательное.
Пример 3
Как будет представлено в памяти компьютера число 26 ?
1) Переводим число 26 в двоичную систему:
2) Допишем слева недостающие нули, так чтобы в представлении числа было ровно 8 цифр:00011010.
3) 26 – число положительное (левый бит равен 0), значит, его дополнительный код равен двоичному представлению, т.е. 00011010
Ответ: 26 будет представлено в памяти компьютера как 00011010.
Пример 4
Как будет представлено в памяти компьютера число –18 ?
1) Переведем модуль числа –18 в двоичную систему:
2) Допишем слева недостающие нули так, чтобы в представлении числа было равно 8 цифр: 00010010.
3) –18 число отрицательное. Определим его дополнительный код
а) меняем нули на единицы, а единицы на нули:
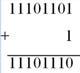
б) к получившемуся числу прибавляем 1: ;
Ответ: –18 будет представлено в компьютере как 11101110.
Пример 5
Что означает число 11011, хранящееся в памяти компьютера?
1) Допишем слева недостающие нули, так чтобы было ровно 8 цифр: 00011011
2) Это число положительное, его дополнительный код совпадает с двоичным представлением
3) Переведем число 11011 из двоичной системы в десятичную: 1 × 24 + 1 × 23 + 0 × 22 + 1 × 20 = 16 + 8 + 2 + 1 = 27
Ответ: число 11011 означает 27.
Пример 6
Что означает число 11110111, хранящееся в памяти компьютера?
1) Допишем слева недостающие нули, так чтобы число содержало 8 цифр (здесь и так 8 цифр, ничего дописывать не надо): 11110111;
2) Это число отрицательное, значит, надо от дополнительного кода, в котором число представлено в памяти компьютера, перейти к двоичному представлению:
а) меняем нули на единицы, а единицы на нули: 11110111 – > 00001000

б) к получившемуся числу прибавляем 1 ;
3) Получившееся число переводим
в десятичную систему:
1 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0 = 8 + 1 = 9 ;
4) Мы нашли модуль числа, но у нас число отрицательное, значит, надо перед числом поставить знак «–», получим – 9 .
Ответ: число 11110111 означает – 9.
Пример 7
Что означает число 9616 ?
1) Переведем в двоичную систему: 9216 – 100100102 ;
2) Число отрицательное, перейдем от дополнительного кода к двоичному представлению:
в десятичную систему
1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 0 × 2 0 =

= 64 + 32 + 8 + 4 + 2 = 110;
4) Число отрицательное, ставим перед ним знак « – ».
Ответ: 9216 означают число – 110.
Пример 8
Для представления числа в памяти компьютера используются 32 байта. Как будет представлено в памяти компьютера – 37?
Запишем дополнительный код числа – 37, интерпретируя его как величину типа LongInt (тридцатидвухбитовое со знаком):
1. Прямой код числа 37 есть 00000000000000000000000000100101;
2. Инверсный код 11111111111111111111111111011010;
3. Дополнительный код 11111111111111111111111111011011 или FFFFFFDB(16).
Пример 9
Запишем числа, соответствующие дополнительным кодам:
1. 0000000000010111. Поскольку в старшем разряде записан нуль, то результат будет положительным. Это код числа 23;
2. 1111111111000000. Здесь записан код отрицательного числа. Исполняем алгоритм:
Пример 10
Выполнить арифметическое действие 300010– 500010в 16-разрядном компьютерном представлении.
Представим положительное число в прямом, а отрицательное число в дополнительном коде:

Сложим прямой код положительного числа с дополнительным кодом отрицательного числа. Получим результат в дополнительном коде:

Переведем полученный дополнительный код в десятичное число:
1) инвертируем дополнительный код: 0000011111001111;
2) прибавим к полученному коду 1 и получим модуль отрицательного числа:

;
3) переведем в десятичное число и припишем знак отрицательного числа: – 2000.
Итак все что хранится в памяти компьютера представлено в виде чисел
Существуют два способа представления чисел в памяти ЭВМ. Они называются так: форма с фиксированной точкой и форма с плавающей точкой. Форма с фиксированной точкой применяется к целым числам, форма с плавающей точкой — к вещественным числам (целым и дробным). Под точкой здесь подразумевается знак-разделитель целой и дробной части числа.
Разберемся, как представляются отрицательные числа. Казалось бы, для этого достаточно заменить 0 на 1 в старшем (31-м) разряде ячейки памяти. Однако реально это делается несколько сложнее. Для представления отрицательных целых чисел используется дополнительный код.

Дополнительным кодом двоичного числа X в N-разрядной ячейке является число, дополняющее его до значения 2.
-
Получить дополнительный код можно следующим путем:
- записать внутреннее представление положительного числа X;
- записать обратный код этого числа заменой во всех разрядах 0 на 1 и 1 на 0;
- к полученному числу прибавить 1.
-
Определим по этим правилам внутреннее представление числа -562810 в 32-разрядной ячейке.
-
00000000 00000000 00010101 1111110 -
11111111 11111111 11101010 00000011 -
11111111 11111111 11101010 00000100
Шестнадцатеричная форма результата:
Старший разряд в представлении любого отрицательного числа равен 1. Следовательно, он указывает на знак числа и поэтому называется знаковым разрядом.
Почему отрицательные числа представляются в дополнительном коде? Дело в том, что в этом случае операция вычитания двух чисел сводится к сложению с дополнительным кодом вычитаемого, и процессору достаточно уметь лишь складывать числа. В самом деле:
Если значение (-В) будет иметь форму дополнительного кода, то в памяти ЭВМ получится правильный результат.
Проверим, действительно ли в ячейке памяти получится О в результате сложения числа 5628 с числом -5628 в форме дополнительного кода.
00000000 00000000 00010101 11111100 + 11111111 11111111 11101010 000000100 =
1 00000000 00000000 00000000 00000000
Что и требовалось доказать! Единица в старшем разряде, получаемая при сложении, выходит за границу разрядной сетки машинного слова и исчезает.
Двоичное 32-разрядное число 231 является «отрицательным самому себе». Получим его дополнительный код:
Полученный код используется для представления значения
Следовательно, диапазон представления целых чисел в 32-разрядном машинном слове:
В общем случае для N-разрядного машинного слова этот диапазон такой:
В современных компьютерах часто используется 16- разрядное представление целых чисел. В этом случае их диапазон следующий:
Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с фиксированной точкой не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.
Вещественные числа. Числовые величины, которые могут принимать любые значения (целые и дробные) называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с веществен-ными числами. Как же такие числа представляются в памяти компьютера?

Вещественные числа в памяти компьютера представляются в форме с плавающей точкой.
Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:
Например, число 25,324 можно записать в таком виде: 0.25324х102. Здесь m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка».
Однако справедливы и следующие равенства:
25,324 = 2,5324*101 = 0,0025324*104 = 2532,4*102 и т.п.
Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализован-ном представлении должна удовлетворять условию:
Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит для рассмотренного числа нормализованным представлением будет: 0.25324 * 102. В разных типах ЭВМ применяются различные варианты представления чисел в форме с плавающей точкой. Для примера рассмотрим один из возможных. Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы. Вот как эта информация располагается в ячейке:
| ± машинный порядок |         М А | Н Т И С | С А      |
     1-й байт                    2-й байт    3-й байт   4-й байт  
В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы.
Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:
| Машинный порядок | 0 | 1 | 2 | 3 | . | 64 | 65 | . | 125 | 126 | 127 |
| Математический порядок | -64 | -63 | -62 | -61 | . | 0 | 1 | . | 61 | 62 | 63 |
Если обозначить машинный порядок Мр, а математический — р, то связь между ними ыразится такой формулой:
Итак, машинный порядок смещен относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает.
Полученная формула записана в десятичной системе. Поскольку 6410=4016 (проверьте!), то в шестнадцатеричной системе формула примет вид:
И, наконец, в двоичной системе:
-
Теперь мы можем записать внутреннее представление числа 25,324 в форме с плавающей точкой.
- Переведем его в двоичную систему счисления с 24 значащими цифрами. 25,32410= 11001,01010010111100011012
- Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,110010101001011110001101*10 101 Здесь мантисса, основание системы счисления (210=102) и порядок (510=1012)записаны в двоичной системе.
- Вычислим машинный порядок. Мр2 = 101 + 100 0000 = 100 0101
- Запишем представление числа в ячейке памяти.
01000101 11001010 10010111 10001101
Это и есть искомый результат. Его можно переписать в более компактной шестнадцатеричной форме:
| 45 | CA | 97 | 8D |
Для того, чтобы получить внутреннее представление отрицательного числа -25,324,достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.
| 11000101 | 11001010 | 10010111 | 10001101 |
А в шестнадцатеричной форме:
| C5 | CA | 97 | 8D |
Никакого инвертирования, как для отрицательных чисел с фиксированной точкой, здесь не происходит.
Рассмотрим, наконец, вопрос о диапазоне чисел, представимых в форме с плавающей точкой. Очевидно, положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим порядком:
Если перевести в десятичную систему, то получится
Rmax = (1 — 2 -24 ) * 2 64 = 10 19
Очевидно, что диапазон вещественных чисел значительно шире диапазона целых чисел. Если в результате вычислений получается число по модулю большее, чем Rmax, то происходит прерывание работы процессора. Такая ситуация называется переполнением при вычислениях с плавающей точкой. Наименьшее по модулю ненулевое значение равно:
Любые значения, меньшие данного по абсолютной величине, воспринимаются процессором как нулевые.
Как известно из математики, множество действительных чисел бесконечно и непрерывно. Множество же вещественных чисел, представимых в памяти ЭВМ в форме с плавающей точкой, является ограниченным и дискретным. Каждое следующее значение получается прибавлением к мантиссе предыдущего единицы в последнем (24-м) разряде. Количество вещественных чисел, точно представимых в па-мяти машины, вычисляется по формуле:
N = 2 t * ( U — L+ 1) + 1.
Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, L = -64) получается:
N = 2 146 683 548.
Все же остальные числа, не попадающие в это множество, но находящиеся в диапазоне допустимых значений, представляются в памяти приближенно (мантисса обрезается на 24-м разряде). А поскольку числа имеют погрешности, то и результаты вычислений с этими числами также будут содержать погрешность. Из сказанного следует вывод: вычисления с вещественными числами в компьютере выполняются приближенно.