Хранение вещественных чисел в памяти компьютера

Учитель информатики

Информатика. 10 класса. Босова Л.Л. Оглавление

§13. Представление чисел в компьютере

Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).

Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.

Представление вещественных чисел

Любое вещественное число А может быть записано в экспоненциальной форме:

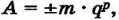
где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Например, число 472 ООО ООО может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.

Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».

Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 10 9 .

Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа:

0,11111111111111111111111 • 10 1111111

Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

Немного истории

В 60-е и 70-е годы не было единого стандарта представления чисел с плавающей запятой, способов округления, арифметических операций. В результате программы были крайне не портабельны. Но еще большей проблемой было то, что у разных компьютеров были свои «странности» и их нужно было знать и учитывать в программе. Например, разница двух не равных чисел возвращала ноль. В результате выражения «X=Y» и «X-Y=0» вступали в противоречие. Умельцы обходили эту проблему очень хитрыми трюками, например, делали присваивание «X=(X-X)+X» перед операциями умножения и деления, чтобы избежать проблем.

Инициатива создать единый стандарт для представления чисел с плавающей запятой подозрительно совпала с попытками в 1976 году компанией Intel разработать «лучшую» арифметику для новых сопроцессоров к 8086 и i432. За разработку взялись ученые киты в этой области, проф. Джон Палмер и Уильям Кэхэн. Последний в своем интервью высказал мнение, что серьезность, с которой Intel разрабатывала свою арифметику, заставила другие компании объединиться и начать процесс стандартизации.

Все были настроены серьезно, ведь очень выгодно продвинуть свою архитектуру и сделать ее стандартной. Свои предложения представили компании DEC, National Superconductor, Zilog, Motorola. Производители мейнфреймов Cray и IBM наблюдали со стороны. Компания Intel, разумеется, тоже представила свою новую арифметику. Авторами предложенной спецификации стали Уильям Кэхэн, Джероми Кунен и Гарольд Стоун и их предложение сразу прозвали «K-C-S».

Практически сразу же были отброшены все предложения, кроме двух: VAX от DEC и «K-C-S» от Intel. Спецификация VAX была значительно проще, уже была реализована в компьютерах PDP-11, и было понятно, как на ней получить максимальную производительность. С другой стороны в «K-C-S» содержалось много полезной функциональности, такой как «специальные» и «денормализованные» числа (подробности ниже).

В «K-C-S» все арифметические алгоритмы заданы строго и требуется, чтобы в реализации результат с ними совпадал. Это позволяет выводить строгие выкладки в рамках этой спецификации. Если раньше математик решал задачу численными методами и доказывал свойства решения, не было никакой гарантии, что эти свойства сохранятся в программе. Строгость арифметики «K-C-S» сделала возможным доказательство теорем, опираясь на арифметику с плавающей запятой.

Компания DEC сделала все, чтобы ее спецификацию сделали стандартом. Она даже заручилась поддержкой некоторых авторитетных ученых в том, что арифметика «K-C-S» в принципе не может достигнуть такой же производительности, как у DEC. Ирония в том, что Intel знала, как сделать свою спецификацию такой же производительной, но эти хитрости были коммерческой тайной. Если бы Intel не уступила и не открыла часть секретов, она бы не смогла сдержать натиск DEC.

Подробнее о баталиях при стандартизации смотрите в интервью профессора Кэхэна, а мы рассмотрим, как выглядит представление чисел с плавающей запятой сейчас.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Денормализованное представление

Для представления очень малых величин, используется так называемое денормализованное или субнормальное представление.

Если все биты порядка установлены в ноль, то это денормализованное число. Для этих чисел, целая часть мантиссы (цифра перед запятой) считается равной нулю, а порядок считается минимальным (не нулевым!). Это позволяет представлять величины меньшие минимального порядка, включая ноль (при нулевой мантиссе).

Представление в памяти денормализованных значений

(s)

(0)

(ldots)

(0)

(m_)

(ldots)

(m_0)

Где (s) – знак числа ( (0) для (+) и (1) для (-) ), (m_ ldots m_0) – дробная часть мантиссы.

Число (a) , хранимое таким образом, можно вычислить как [a = (s) left(sum_^ m_i 2^ right) cdot 2^>]

Следует заметить, что “ноль” может иметь знак: “+0” и “-0”. Связано это с тем, что очень малые числа ввиду погрешности округления имеют нулевую мантиссу – в таких случаях полезно по крайней мере сохранять информацию о знаке.

Другие специальные значения включают “бесконечность” и “не число”.

Бесконечность получается, если все биты порядка равны 1, а биты мантиссы – 0.

Представление в памяти значений “бесконечность”

(s)

(1)

(ldots)

(1)

(0)

(ldots)

(0)

“Не число” (NaN) получается, если все биты порядка равны 1, а биты мантиссы не все равны 0.

Представление в памяти значений “NaN”, (exists iin[0;;r-1]: m_ineq 0)

(s)

(1)

(ldots)

(1)

(m_)

(ldots)

(m_0)

Нормальная и нормализованная форма

Нормальной формой числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале [0; 1). Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать в 4 формах — 0,0001×10 0 , 0,001×10 −1 , 0,01×10 −2 , 0,1×10 −3 ), поэтому распространена также другая форма записи —нормализованная, в которой мантисса десятичного числа принимает значения от 1 (включительно) до 10 (не включительно), а мантисса двоичного числа принимает значения от 1 (включительно) до 2 (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме 0) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа 0 (а заодно и некоторых других полезных чисел, таких как и ).

$pminfty$

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, «не число», получается как результат операций типа деления нуля на ноль) и .

Название	Тип в языке программирования C	Диапазон	Биты мантиссы	Биты
Half precision	Нет	6,10×10 -5 ..65504	10+1	16
Single precision	float	3,4×10 -38 ..3,4×10 38	23+1	32
Double precision	double	1,7×10 -308 ..1,7×10 308	52+1	64

Представление чисел

Сначала поясним на образном примере, что такое дискретность.

Дискретное множество состоит из отделенных друг от друга элементов. Например, песок дискретен, поскольку он состоит из отдельных песчинок. А вода или масло непрерывны (в рамках наших ощущений, поскольку отдельные молекулы мы всё равно ощутить не можем). Этот пример нужен нам только для аналогии. Здесь мы не станем углубляться в изучение материального мира, а вернемся к предмету изучения информатики — информации.

Самым традиционным видом данных, с которым работают компьютеры, являются числа. ЭВМ первого поколения умели решать только математические задачи. Люди начали работать с числами еще с первобытных времен. Первоначально человек оперировал лишь целыми положительными (натуральными) числами: 1, 2, 3, 4, . . Очевидно, что натуральный ряд — это дискретное множество чисел.

В математике ряд натуральных чисел бесконечен и не ограничен. С появлением в математике понятия отрицательного числа (Р. Декарт, XVII век в Европе; в Индии значительно раньше) оказалось, что множество целых чисел не ограничено как «справа», так и «слева». Покажем это на числовой оси (рис. 1.6), символы оо обозначают бесконечность.

Рис. 1.6. Математическое множество целых чисел на числовой оси

Из сказанного следует вывод: множество целых чисел в математике дискретно и не ограничено. Отметим еще один факт: разность соседних чисел натурального ряда (данного и предыдущего) всегда равна единице. Эту величину назовем шагом числовой последовательности.

Любое вычислительное устройство (компьютер, калькулятор) может работать только с ограниченным множеством целых чисел. Возьмите в руки калькулятор, на индикаторном табло которого помещается 10 знаков. Самое большое положительное число, которое на него поместится:

Самое большое по абсолютной величине (модулю)

Аналогично дело обстоит и в компьютере.

Представление вещественных чисел

472000000=4,72⋅10 8
472000000=47,2⋅10 7
472000000=472,0⋅10 6

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида:4,72E+8.

Здесь знак E обозначает основание десятичной системы счисления и читается как «умножить на десять в степени». Из приведённого выше примера видно, что положение запятой в записи числа может изменяться. Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472000000 будет представлено как 0,472⋅10 9 .

Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядки и мантиссы. Пример:

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂=127₁₀ и, следовательно, максимальное значение числа: 0,11111111111111111111111⋅10 1111111 .