Представление чисел в формате с плавающей запятой в двоичной системе счисления

Представление чисел с плавающей точкой

Математическая запись числа две целых четыре сотых выглядит так 2,04 но возможна и такая запись 0,204×10, или такая 20,4×10 -1 , или такая 0,0204×10 2 . Этот ряд можно продолжать сколь угодно долго. На что вы обратили внимание? — запятая перемещается («плавает») влево или вправо, и, чтобы не изменить значение числа, мы умножаем его на 10 в отрицательной или положительной степени.

Для представления вещественных чисел в памяти ЭВМ используется формат с плавающей точкой. При этом необходимо помнить, что система вещественных чисел представимых в ЭВМ является дискретной и конечной.

В общем случае любое число N, представляемое в форме с плавающей точкой, является произведением двух сомножителей: .

m — мы будем называть мантиссой числа (модуль целой части мантиссы изменяется в диапазоне от 1 до S-1 (включая эти числа), где S- основание системы счисления),

p — целочисленный порядок,

S ¾ основание системы счисления.

Различают нормализованную и экспоненциальную формы записи числа. Если мантисса является правильной дробью, у которой первая цифра после точки отлична от нуля , то число называется нормализованным.

При представлении числа в экспоненциальной форме обязательно присутствует целая часть, содержащая не более одной цифры отличной от нуля, фактически эта форма представления совпадает со стандартной математической формой записи числа.

Вещественное число в ПЭВМ представлено в экспоненциальной форме.

Следовательно, при представлении чисел с плавающей точкой необходимо записать в разрядной сетке ЭВМ со своими знаками мантиссу и порядок . Знак числа при этом совпадает со знаком мантиссы. Запишем число 314.6789 в экспоненциальной форме:314.6789= 3.1467890000E+2. Число разрядов, выделенных для изображения порядков, определяет диапазон представимых в ЭВМ чисел с плавающей точкой.

Кроме того, этот диапазон зависит также от основания S принятой системы счисления.

Значение произвольного числа вещественного типа представляется в ПЭВМ лишь с некоторой конечной точностью, которая зависит от внутреннего формата вещественного числа, точность представления чисел повышается с увеличением числа разрядов мантиссы.

Для того, чтобы упростить операции над порядками их сводят к действиям над целыми положительными числами путем использования так называемого смещенного порядка, который всегда положителен. смещенный порядок получается путем прибавления к порядку р некоторого целого положительного числа, значение которого зависит от конкретного формата данных.

Десятичная точка подразумевается перед левым (старшим) разрядом мантиссы, но при действиях с числом ее положение смещается влево или вправо в зависимости от двоичного порядка.

Рассмотрим представление чисел в разрядной сетке длиной 4 байта ( так называемая одинарная точность). Изобразим разрядную сетку, состоящую из 32 разрядов и посмотрим, как эти разряды распределены.

0 1 2 3 4 5 6 7 8 … 31

знак мантиссы порядок мантисса

Пусть необходимо представить число –13,75 в разрядной сетке с одинарной точностью. Для этого необходимо выполнить следующие действия:

1. перевести число в двоичную систему счисления;

2. представить его в экспоненциальной форме;

3. получить исходный порядок и мантиссу;

4. получить смещенный порядок.

2) Представим двоичное число 1101.11 в экспоненциальной форме 1101.11=1.10111E+3.

3) Исходный порядок равен 3.

Следует отметить, что целая часть двоичного числа представленного в экспоненциальной форме, всегда равна 1, поэтому в целях экономии разрядов (а следовательно увеличения диапазона представления чисел)целая часть числа не записывается в разрядную сетку.

4) Вычислим смещенный порядок (в формате с одинарной точностью к исходному порядку добавляется число 127)

Pсм=3+127=130=128+2=2 7 +2=10000000₂+102=1000 0010₂

Знак числа положительный, следовательно, самый левый разряд равен 0.

0 10000010 10111000000000000000000

знак порядок мантисса

представим полученное число в шестнадцатеричной системе счисления

0100 0001 0101 1100 0000 0000 0000 0000

Итак, мы получили шестнадцатеричное число 415С0000.

Решим обратную задачу.

Значение переменной А Представлено в формате с плавающей точкой в шестнадцатеричной системе счисления А=ВЕ200000. Тип переменной А-single для языка Паскаль. Найти десятичное значение переменной А.

Для решения обратной задачи необходимо выполнить следующие действия:

1) Перевести шестнадцатеричное число в двоичную систему счисления.

2) Выделить знак мантиссы(знак мантиссы совпадает со знаком числа).

3) Выделить смещенный порядок.

4) Вычислить исходный порядок.

5) Записать число, не забыв указать его целую часть, в экспоненциальной форме.

6) Перевести число из экспоненциальной формы в обычную форму записи.

7) Перевести число из двоичной системы счисления в десятичную.

Выполним перечисленные действия.

ВЕ200000=1011 1110 0010 0…0000

1 01111100 0100…0

знак порядок мантисса

Число отрицательное так как левый разряд равен 1.

Вычислим исходный порядок:

Запишем искомое число в экспоненциальной форме в двоичной системе счисления:

А=-1.01Е-3. Не забывайте указывать целую часть.

Представим искомое число в обычной форме записи в двоичной системе счисления:

Операция алгебраического сложения чисел, представленных в форме с плавающей точкой , производится несколько сложнее, чем для чисел, представленных в форме с фиксированной точкой. При выполнении ее сначала выравниваются порядки слагаемых, В результате сравнения порядков порядок меньшего по модулю числа принимается равным порядку большего, а его мантисса сдвигается вправо на число шестнадцатеричных разрядов, равное разности порядков.

В процессе сдвига мантиссы меньшего слагаемого происходит потеря младших разрядов, что вносит определенную погрешность в результат выполнения данной операции.

После выравнивания порядков производится алгебраическое сложение мантисс.

Выполнить самостоятельно:

1) Найти представление десятичного числа А в шестнадцатеричной системе счисления в формате с плавающей точкой. Тип числа single.

А=-357.2265626; А=-0.203125; А=998.46875;

А=–657.4375; А=998.8125; А=-905,34375; А=897.5625

А=637.65625; А=56.53125; А=-4.78125.

2) Значение переменной А представлено в формате с плавающей точкой в шестнадцатеричной системе счисления. Тип переменной А-single для языка Паскаль. Найти десятичное значение переменной А.

Представление чисел в формате с плавающей запятой в двоичной системе счисления

Действительные или вещественные числа часто используются в математических вычислениях и представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Однако в компьютерах числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютерном представлении выступают как приближенные.

Любое вещественное число можно записать в нормальной (научной, экспоненциальной) форме:

, (2.5.)

где – мантисса числа; – основание системы счисления; – порядок.

Порядок указывает, на какое количество позиций и в каком направлении должна сместиться в мантиссе точка (запятая), отделяющая дробную часть от целой.

С целью минимизации погрешности в вычислениях и эффективного использования памяти, а также в соответствии со стандартом IEEE-754[1], если мантисса находится в диапазоне , то число считается нормализованным. Именно такое представление числа с плавающей запятой и используется в компьютере. Это экономит один бит, так как неявная единица в памяти не хранится.

Замечание. Из нормализованного представления следует, что дробная часть мантиссы должна удовлетворять условию: .

Теперь можно сказать, что нормализованное число имеет следующий вид:

(2.6.)

Рассмотрим примеры представления любого числа в форме плавающей запятой:

1) 12,345₍₁₀₎ = 0,0012345₍₁₀₎ * 10 4 = 0,12345₍₁₀₎ * 10 2 = 1234, 5₍₁₀₎ * 10 -2

2) 101110,11101₍₂₎ = 0,10111011101₍₂₎*10 6 = 0,010111011101₍₂₎*10 7

Из приведенных примеров можно сделать следующие выводы:

· порядок числа определяет, на сколько разрядов необходимо осуществить сдвиг относительно запятой;

· представление чисел в форме с плавающей запятой неоднозначно.

Стандарт IEEE-754 определяет четыре основных «двоичных» формата чисел с плавающей запятой (Таблица 2.5).

Формат	Точность	Число бит	Порядок	Смещение порядка	Мантисса	Число знаков после запятой
binary 16	half
binary 32	single
binary 64	double
binary 128	quadruple

Наиболее часто используемые форматы вещественных чисел являются: с одинарной точностью (single-precision, 32 бита); с двойной точностью (double-precision, 64 бита).

Как нормализованное число, записанное в форме с плавающей запятой, записывается в память, представлено на схемах для 32-х разрядных (Рисунок 2.2) и 64-х разрядных чисел (Рисунок 2.3).

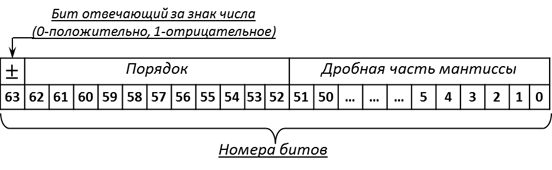
Первое поле, занимающее один бит с номером 31 (63), отвечает за знак числа. Второе, занимающее биты с 23-го по 30-й (с 52-го по 62-й), относится к порядку числа (или экспоненте). В стандарте IEEE-754 указано, что в этом поле сохраняется смещенный порядок. Смещенный порядок (M_(n)) или смещенная экспонента, указанный на схемах связаны с обычным порядком (p) числа соотношением

, (2.7.)

где означает «смещение» и выбирается для разных форматов чисел таким образом, чтобы значение выражения (2.7.) всегда было положительно. Такой подход вызван тем обстоятельством, что знак порядка, который может быть как положительным, так и отрицательным, в компьютерном представлении числа не хранится Значение смещения для чисел различны разной разрядности указаны в Таблице 2.5. Последнее поле, занимающее 23 (52) бита от 0-го до 22-го (от 0-го до 51-го) хранит мантиссу, точнее, её дробную часть, потому как бит целой части не хранится.

Пример: Запишем внутреннее представление числа в форме с плавающей точкой в формате 32 бит.

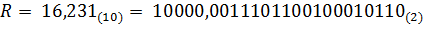
1. Переведем его в двоичную систему счисления с 24 значащими цифрами.

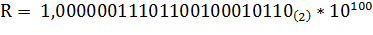
2. Запишем в форме нормализованного двоичного числа с плавающей точкой:

3. Здесь мантисса, основание системы счисления (2₍₁₀₎=10₍₂₎) и порядок (4₍₁₀₎=100₍₂₎)записаны в двоичной системе.

4. Вычислим машинный порядок.

5. Таким образом, в двоичном коде с плавающей запятой число примет вид:

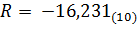
Для того, чтобы получить внутреннее представление отрицательного числа , достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.

Теперь переведем полученное число обратно в десятичный формат.

По виду конечного результата очевидна погрешность ( ) в представлении двоичных чисел с плавающей запятой. В этом состоит главная особенность обработки вещественных чисел в компьютере — она всегда ведется с погрешностью [Стариченко].

[1] стандарт IEEE (Institute of Electrical and Electronics Engineers), описывающий формат представления чисел с плавающей точкой

Представление чисел в памяти компьютера с плавающей запятой

Представление чисел в формате с фиксированной запятой. Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а «запятая» «находится» справа после младшего разряда, то есть вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А₂ = = 11110000₂ будет храниться в ячейке памяти следующим образом:

1

1

1

1

0

0

0

0

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате целых неотрицательных чисел. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно нулю. Максимальное число соответствует восьми единицам и равно

А = 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 = 1 × 2 8 — 1 = 255₁₀.

Диапазон изменения целых неотрицательных чисел чисел: от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 битов), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1).

Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа. Например, число 2002₁₀ = 11111010010₂ будет представлено в 16-разрядном представлении следующим образом:

0

0

0

0

0

1

1

1

1

1

0

1

0

0

1

0

Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-разрядном представлении равно:

Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.

Дополнительный код отрицательного числа А, хранящегося в n ячейках, равен 2 n — |A|.

Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, так как в n-разрядной компьютерной арифметике:

поскольку в компьютерной n-разрядной арифметике 2 n = 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, то есть n нулей.

Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:

1. Модуль числа записать в прямом коде в n двоичных разрядах.

2. Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).

3. К полученному обратному коду прибавить единицу.

Запишем дополнительный код отрицательного числа -2002 для 16-разрядного компьютерного представления:

При n-разрядном представлении отрицательного числа А в дополнительным коде старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число

Чтобы число было положительным, должно выполняться условие

Следовательно, максимальное значение модуля числа А в га-разрядном представлении равно:

Тогда минимальное отрицательное число равно:

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится четыре ячейки памяти — 32 бита).

Максимальное положительное целое число (с учетом выделения одного разряда на знак) равно:

А = 2 31 — 1 = 2 147 483 647₁₀.

Минимальное отрицательное целое число равно:

А = -2 31 = — 2 147 483 648₁₀.

Достоинствами представления чисел в формате с фиксированной запятой являются простота и наглядность представления чисел, а также простота алгоритмов реализации арифметических операций.

Недостатком представления чисел в формате с фиксированной запятой является небольшой диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.

Представление чисел в формате с плавающей запятой. Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. В этом случае положение запятой в записи числа может изменяться.

Формат чисел с плавающей запятой базируется на экспоненциальной форме записи, в которой может быть представлено любое число. Так число А может быть представлено в виде:

A = m × q n

2.3

где m — мантисса числа;
q — основание системы счисления;
n — порядок числа.

Для единообразия представления чисел с плавающей запятой используется нормализованная форма, при которой мантисса отвечает условию:

Здесь нормализованная мантисса: m = 0,55555, порядок: n = 3.

Число в формате с плавающей запятой занимает в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности). При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Диапазон изменения чисел определяется количеством разрядов, отведенных для хранения порядка числа, а точность (количество значащих цифр) определяется количеством разрядов, отведенных для хранения мантиссы.

Определим максимальное число и его точность для формата чисел обычной точности, если для хранения порядка и его знака отводится 8 разрядов, а для хранения мантиссы и ее знака — 24 разряда:

0	1	1	1	1	1	1	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
знак и порядок								знак и мантисса

Максимальное значение порядка числа составит 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа составит:

2 127 = 1,7014118346046923173168730371588 × 10 38 .

Максимальное значение положительной мантиссы равно:

2 23 — 1 » 2 23 = 2 (10 × 2,3) » 1000 2,3 = 10 (3 × 2,3) » 10 7 .

Таким образом максимальное значение чисел обычной точности с учетом возможной точности вычислений составит 1,701411 × 10 38 (количество значащих цифр десятичного числа в данном случае ограничено 7 разрядами).

1.26. Заполнить таблицу, записав отрицательные десятичные числа в прямом, обратном и дополнительном кодах в 16-разрядном представлении:

Десятичные числа	Прямой код	Обратный код	Дополнительный код
-50
-500

1.27. Определить диапазон представления целых чисел со знаком (отводится 2 байта памяти) в формате с фиксированной запятой.

1.28. Определить максимальное число и его точность для формата чисел двойной точности, если для хранения порядка и его знака отводится 11 разрядов, а для хранения мантиссы и ее знака — 53 разряда.

Вещественные числа в компьютере

Понятие вещественного (действительного) числа в математику ввел Исаак Ньютон в XVIII веке. В математике множество вещественных чисел непрерывно, бесконечно и не ограничено. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел, что и означает непрерывность множества.

Как мы говорили выше, числа в компьютере (в том числе и вещественные) представлены в двоичной системе счисления. Покажем, что множество вещественных чисел в компьютере дискретно, ограничено и конечно. Нетрудно догадаться, что это, так же как и в случае целых чисел, вытекает из ограничения размера ячейки памяти.

Снова для примера возьмем калькулятор с десятиразрядным индикаторным табло. Экспериментально докажем дискретность представления вещественных чисел. Выполним на калькуляторе деление 1 на 3. Из математики вам известно, что 1/3 — это рациональная дробь, представление которой в виде десятичной дроби содержит бесконечное количество цифр: 0,3333333333. (3 в периоде). На табло калькулятора вы увидите:

Первый разряд зарезервирован под знак числа. После запятой сохраняется 8 цифр, а остальные не вмещаются в разрядную сетку (так это обычно называют). Значит, это не точное значение, равное 1/3, а его «урезанное» значение.

Следующее по величине число, которое помещается в разрядную сетку:

Оно больше предыдущего на 0,00000001. Это шаг числовой последовательности. Следовательно, два рассмотренных числа разделены между собой конечным отрезком. Очевидно, что предыдущее число такое:

Оно тоже отделено от своего «соседа справа» по числовой оси шагом 0,00000001. Отсюда делаем вывод: множество вещественных чисел, представимых в калькуляторе, дискретно, поскольку числа отделены друг от друга конечными отрезками.

А теперь выясним вот что: будет ли шаг в последовательности вещественных чисел на калькуляторе постоянной величиной (как у целых чисел)?

Вычислим выражение 100000/3. Получим:

Это число в 100 000 раз больше предыдущего и, очевидно, тоже приближенное. Легко понять, что следующее вещественное число, которое можно получить на табло калькулятора, будет больше данного на 0,0001. Шаг стал гораздо больше.

Отсюда приходим к выводу: множество вещественных чисел, представимых в калькуляторе, дискретно с переменной величиной шага между соседними числами.

Если отметить на числовой оси точные значения вещественных чисел, которые представимы в калькуляторе, то эти точки будут расположены вдоль оси неравномерно. Ближе к нулю — чаще, дальше от нуля — реже (рис. 1.8).

Рис. 1.8. Условное представление взаимного расположения множества вещественных чисел, представимых в компьютере

Все выводы, которые мы делаем на примере калькулятора, полностью переносятся на компьютер с переходом к двоичной системе счисления и с учетом размера ячейки компьютера, отводимой под вещественные числа. Неравномерное расположение вещественных чисел, представимых в компьютере, также имеет место.

Ответим на вопрос: ограничено ли множество вещественных чисел в памяти компьютера? Если продолжать эксперименты с калькулятором, то ответ на этот вопрос будет таким: да, мнолсест-во вещественных чисел в калькуляторе ограничено. Причиной тому служит все та же ограниченность разрядной сетки. Отсюда же следует и конечность множества.

Самое большое число у разных калькуляторов может оказаться разным. У самого простого это будет то же число, что мы получали раньше: 999999999. Если прибавить к нему единицу, то калькулятор выдаст сообщение об ошибке. А на другом, более «умном» и дорогом, калькуляторе прибавление единицы приведет к такому результату:

Данную запись на табло надо понимать так: 1 • 10 9 .

Такой формат записи числа называется форматом с плавающей запятой, в отличие от всех предыдущих примеров, где рассматривалось представление чисел в формате с фиксированной запятой.

Число, стоящее перед буквой «е», называется мантиссой, а стоящее после — порядком. «Умный» калькулятор перешел к представлению чисел в формате с плавающей запятой после того, как под формат с фиксированной запятой не стало хватать места на табло.

В компьютере то же самое: числа могут представляться как в формате с фиксированной запятой (обычно это целые числа), так и в формате с плавающей запятой.

Но и для формата с плавающей запятой тоже есть максимальное число. В нашем «подопытном» калькуляторе это число:

То есть 99999 • 10 99 . Самое большое по модулю отрицательное значение -99999 • 10 99 . Данные числа являются целыми, но именно они ограничивают представление любых чисел (целых и вещественных) в калькуляторе.

В компьютере всё организовано аналогично, но предельные значения еще больше. Это зависит от разрядности ячейки памяти, выделяемой под число, и от того, сколько разрядов выделяется под порядок и под мантиссу.

Рассмотрим пример: пусть под всё число в компьютере выделяется 8 байтов — 64 бита, из них под порядок — 2 байта, под мантиссу — 6 байтов. Тогда диапазон вещественных чисел, в переводе в десятичную систему счисления, оказывается следующим:

±(5 • 10 -324 — 1,7 • 10 308 ).

Завершая тему, посмотрим на рис. 1.9. Смысл, заложенный в нем, такой: непрерывное, бесконечное и не ограниченное множество вещественных чисел, которое рассматривает математика, при его представлении в компьютере обращается в дискретное, конечное и ограниченное множество.

Рис. 1.9. Представление о множестве вещественных чисел в математике и в информатике

Система основных понятий

Вопросы и задания

1. Почему множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
2. Определите диапазон целых чисел, хранящихся в 1 байте памяти в двух вариантах: со знаком и без знака.
3. Получите внутреннее представление числа 157 в 8-разрядной ячейке памяти в формате со знаком.
4. Получите внутреннее представление числа -157 в 8-разрядной ячейке памяти в формате со знаком.
5. Почему множество действительных (вещественных) чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
6. На какие две части делится число в формате с плавающей запятой?

* Конечно, и «внутри калькулятора» числа представляются в двоичном виде. Однако мы в это вдаваться не будем, рассмотрев лишь внешнее представление. Пример с калькулятором нам нужен был только для иллюстрации проблемы ограниченности.