Логические основы цифровой техники
Все цифровые устройства построены на элементах, которые выполняют те или иные логические операции. Для формального описания логической стороны процессов в цифровых устройствах используется алгебра логики (АЛ).
Алгебра логики оперирует с двоичными переменными, которые условно обозначаются, как логический нуль (лог.О) и логическая единица (лог.1). Между обычной, привычной нам алгеброй и АЛ имеются существенные различия в отношении количества и характера операций, а также законов, которым они подчиняются.
Логические устройства

Для описания законов функционирования цифровых схем используется алгебра логики или булева алгебра. В основу алгебры логики положено понятие «событие», которое может наступить, либо не наступить. Наступившее событие считается истинным и выражается уровнем логической «1» , не наступившее событие считается ложным и выражается уровнем логического «0» .
На событие влияют переменные, причем влияют по определенному закону. Этот закон называется логической функцией , а переменные – аргументами . Т.о. логической функцией является функция у = f(x1, x2,… xn), принимающая значения «0» либо «1». Переменные x1, x2,… xn также имеют значения «0» либо «1».
Алгебра логики — раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов. В формулах алгебры логики переменные являются логическими или двоичными, т. е. принимающими только два значения — ложь и истина, которые обозначаются соответственно 0 и 1. Любая программа для ЭВМ содержит логические операции.
Устройства, предназначенные для формирования функций алгебры логики, называются логическими устройствами . Логическое устройство имеет сколь угодное количество входов и только один выход (рис. 1).
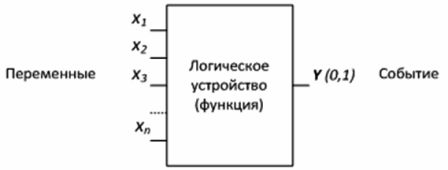
Рисунок 1 – Логическое устройство
Например, в состав электронного кодового замка входит логическое устройство, для которого событие (y) – это открытие замка. Для того чтобы событие произошло (y=1), т.е. замок открылся, необходимо определить переменные – десять кнопок кодонабирателя с цифрами. Определенные кнопки должны быть нажаты, т.е. принять значение «1» и при этом нажаты в определенной последовательности – логическая функция.
Любую логическую функцию удобно представить в виде таблицы состояний (таблицы истинности), где записываются возможные комбинации переменных (аргументов) и соответствующее им значение функции.
Логические устройства строятся на логических элементах, которые реализуют определённую функцию. Базовыми логическими функциями являются логическое сложение, логическое умножение и логическое отрицание.
1) ИЛИ (OR) — логическое сложение или дизъюнкция (от англ. disjunction — разъединение) — на выходе этого элемента появится логическая единица тогда, когда хотя бы на одном из входов появится единица. Логический ноль на выходе будет только тогда, когда на всех входах будет сигнал логического нуля.
Эту операцию можно реализовать с помощью контактной цепи с двумя параллельно включенными контактами. «1» на выходе такой цепи появится в том случае, если хотя бы один из контактов замкнут.
2) И (AND) — логическое умножение или конъюнкция (от англ. conjunction — соединение, & — амперсанд) — на выходе этого элемента сигнал логической единицы появляется только тогда, когда на всех входах будет присутствовать логическая единица. Если хотя бы на одном входе будет ноль, то и на выходе тоже будет ноль.
Эта операция может быть реализована контактной цепью, состоящей из последовательно включённых контактов.
3) НЕ (NOT) — логическое отрицание или инверсия , обозначается черточкой над переменной — операция выполняется над одной переменной x и значение у противоположно этой переменной.
Операция НЕ может быть осуществлена с помощью нормально замкнутого контакта электромагнитного реле: нет напряжения на обмотке реле (x = 0) – контакт замкнут и на выходе «1» (у = 1). При наличии напряжения на обмотке реле (х = 1) контакт разомкнут и на выходе «0» (у = 0).
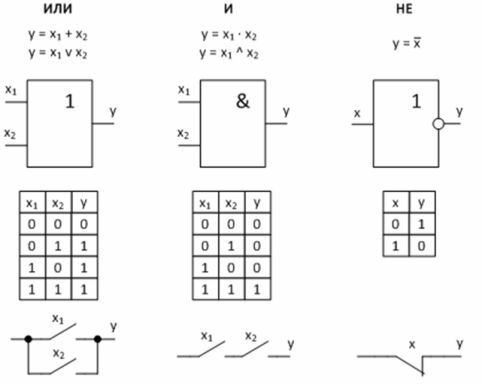
Рисунок 2 – Базовые логические функции и их реализация
В логических устройствах используются различные логические элементы. Особое значение имеют две универсальные логические операции, каждая из которых способна самостоятельно образовать любую логическую функцию.

4) И-НЕ — функция Шеффера .
5) ИЛИ-НЕ — функция Пирса .
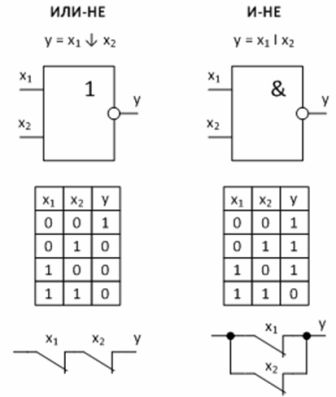
Рисунок 3 – Универсальные логические функции и их реализация
Пример: Схема охранной сигнализации на логических элементах. Генератор Г вырабатывает сигнал сирены, подавая его на усилительный каскад через логический элемент «И» на микросхеме DD2. При замкнутых состояниях охранных ключей S1 – S4 на входах элемента DD1 действует уровень «0» — на нижнем входе элемента «И» DD2 уровень «0», значит на затворе транзистора VT также «0».
В случае размыкания хотя бы одного из ключа, например S1, на вход элемента DD1 через резистор R1 поступит напряжение уровня «1», что приведёт к появлению «1» на втором входе элемента «И» DD1. Это позволит сигналу с генератора Г поступать на затвор транзистора, в нагрузке которого стоит динамик.
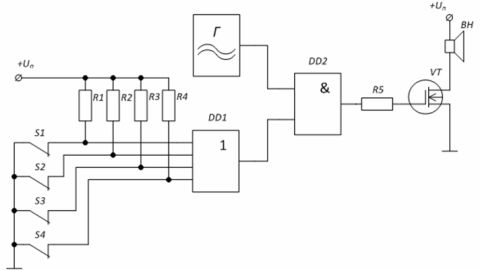
Рисунок 4 – Схема охранной сигнализации
Сложные цифровые схемы строятся путем многократного повторения базовых логических схем. Инструментом такого построения служит булева алгебра, которая применительно к цифровой технике называется алгеброй логики. В отличие от переменной в обычной алгебре логическая переменная имеет только два значения, которые называются логическим нулем и логической единицей.
Логический нуль и логическая единица обозначаются соответственно 0 и 1. В алгебре логики 0 и 1 не числа, а логические переменные. В алгебре логики существуют три основных операции между логическими переменными: логическое умножение (конъюнкция), логическое сложение (дизъюнкция) и логическое отрицание (инверсия).
Электронные схемы, выполняющие одну и ту же логическую функцию, но собранные на различных элементах, отличаются по потребляемой мощности, напряжению питания, значениям высокого и низкого уровней выходного напряжения, времени задержки распространения сигнала и нагрузочной способности.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Алгебра логики
Логика очень древняя наука. Ещё в античные времена была известна формальная логика , позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения. Например, уже в древности был известен закон исключения третьего . Его содержательная трактовка была такова: «Во время своих странствований Платон был в Египте ИЛИ не был Платон в Египте». В такой форме это или любое другое выражение будут правильны (тогда говорили: истинно ). Ничего другого быть не может: Платон либо был, либо не был в Египте — третьего не дано.
Другой закон логики — закон непротиворечивости. Если сказать: «Во время своих странствий Платон был в Египте И не был Платон в Египте», то очевидно, любое высказывание, имеющее такую форму, всегда будет ложно . Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута.
Ещё один закон, известный в древности — закон отрицания: «Если НЕ верно, что Платон НЕ был в Египте, то значит, Платон был в Египте».
Формальная логика основана на “высказываниях”. “Высказывание” — это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит.
Например: Листва на деревьях опадает осенью. Земля прямоугольная.
Первое высказывание содержит истинную информацию, а второе — ложную. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается.
Пример предложений, не являющихся высказываниями: Не пейте сырую воду! Кто не хочет быть счастливым?
Высказывания могут быть и такими: 2>1, Н 2 О+SO 3 =H 2 SO 4 . Здесь используются языки математических символов и химических формул.
Приведённые выше примеры высказываний являются простыми. Но из простых высказываний можно получить сложные, объединив их с помощью логических связок. Логические связки — это слова, которые подразумевают определённые логические связи между высказываниями. Основные логические связки издавна употребляются не только в научном языке, но и в обыденном, — это “и”, “или”, “не”, “если . то”, “либо . либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если . то” для связи простых высказываний в сложные.
Высказывания бывают общими, частными и единичными. Общее высказывание начинается со слов: всё, все, всякий, каждый, ни один. Частное высказывание начинается со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.
Формальная логика была известна в средневековой Европе, она развивалась и обогащалась новыми законами и правилами, но при этом вплоть до 19 века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке.
В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики.
Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно. Трудность изучения алгебры логики возникает из-за того, что для обозначения переменных принимают символы 0 и 1, которые по написанию совпадают с обычными арифметическими единицей и нулём. Но совпадение это только внешнее, так как смысл они имеют совсем иной.
Логическая 1 означает, что какое-то событие истинно, в противоположность этому логический 0 означает, что высказывание не соответствует истине, т.е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).
В алгебре логики знаки операций обозначают лишь три логические связки ИЛИ, И, НЕ.
1.Логическая операция ИЛИ. Логическую функцию принято задавать в виде таблицы. В левой части этой таблицы перечисляются все возможные значения аргументов функции , т.е. входные величины, а в правой указывается соответствующее им значение логической функции. Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид:
Операцию ИЛИ называют также логическим сложением, и потому её можно обозначать знаком «+».
Рассмотрим сложное единичное высказывание: «Летом я поеду в деревню или в туристическую поездку». Обозначим через А простое высказывание «Летом я поеду в деревню», а через В — простое высказывание «Летом я поеду в туристическую поездку». Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.
2. Логическая операция И. Таблица истинности для этой функции имеет вид:
Из таблицы истинности следует, что операция И — это логическое умножение, которое ничем не отличается от традиционно известного умножения в обычной алгебре. Операцию И можно обозначить знаком по-разному:
В формальной логике операции логического умножения соответствуют связки и, а, но, хотя.
3. Логическая операция НЕ. Эта операция является специфичной для алгебры логики и не имеет аналога в обычной алгебре. Она обозначается чертой над значением переменной, либо знаком приставки перед значением переменной:
Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид:
В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ — дизъюнкцией, операцию И — конъюнкцией . Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Рассмотрим некоторые из них.
Логическая операция “строгая дизъюнкция”. Этой логической операции соответствует логическая связка “либо . либо”. Таблица истинности для этой функции имеет вид:
Операция “строгая дизъюнкция” выражается через логические функции “И”, “ИЛИ”, “НЕ” любой из двух логических формул:
и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
Логическая операция “импликация”. Выражение, начинающееся со слов если, когда, коль скоро и продолжающееся словами то, тогда, называется условным высказыванием или операцией «импликация». Таблица истинности для этой функции имеет вид:
Операцию “импликация” можно обозначить по-разному:
Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствуют логические связки “если и только если”, «тогда и только тогда, когда». Таблица истинности для этой функции имеет вид:
Операция “эквивалентность” обозначается по-разному. Выражения
обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы
С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство.
В алгебре логики, как в элементарной, справедливы переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности) законы, а также аксиома идемпотентности (отсутствие степеней и коэффициэнтов) и др., в записях которых используются логические переменные, принимающие только два значения — логический ноль и логическая единица. Применение этих законов позволяет производить упрощение логических функций, т.е. находить для них выражения, имеющие наиболее простую форму. Основные аксиомы и законы алгебры логики приведены в таблице:
Логические элементы
С помощью логических элементов в компьютере реализуются логические функции, которые были рассмотрены ранее.

На выходе конъюнктора будет единица только в том случае, когда на входе будут две единицы, в остальных случаях будет (0).

В результате работы дизъюнктора может получиться (0) тогда и только тогда, когда на входе два нуля.
Логические основы компьютера
Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.
Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.
Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.
Логические операции. Дизъюнкция, конъюнкция и отрицание(инверсия)
Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6». Как мы решаем, что нам сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае правдивости обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным.
Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.

Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, т.к. с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем. Такими операциями являются конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ). Часто конъюнкцию обозначают &, дизъюнкцию — ||, а отрицание — чертой над переменной, обозначающей высказывание.
При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.
При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.
Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.
Таблицы истинности
Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).
Логические основы компьютера
В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.
Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.
Переключательные схемы
В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае — ток проходит, во втором — нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.
Вентиль — это устройство, которое выдает результат булевой операции от введенных в него данных (сигналов). Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.
Вентили представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления арифметических операций, а на основе других строят различную память ЭВМ.
Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот, т.е. получаем вентиль НЕ.
Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕ и И-НЕ. Эти вентили принимают уже не один, а два и более входных сигнала. Выходной сигнал всегда один и зависит от входных сигналов. В случае вентиля ИЛИ-НЕ получить высокое напряжение (логическую единицу) можно только при условии низкого напряжении на всех входах. В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми. Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя.
Выходной сигнал вентиля можно выражать как функцию от входных.
Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.