Почему так сложно создать квантовый компьютер? С белорусским физиком объясняем технологию будущего
Изобретению квантовых компьютеров частенько предсказывают прорыв, аналогичный прорывам при изобретении колеса, покорении огня или создании хорошо знакомых нам компьютеров. Но пока с этой задачей в полном масштабе никто справиться не сумел. В чем же основная загвоздка и зачем нам квантовые компьютеры? Сегодня Onliner.by объясняет суть компьютеров будущего, а помогает нам в этом заместитель заведующего Центром квантовой оптики и информатики Института физики НАН Беларуси член-корреспондент Дмитрий Могилевцев.
Зачем вести разработки по созданию квантовых компьютеров? Чем нас не устраивают нынешние, которые постоянно прогрессируют в своей мощности? Теоретически квантовые компьютеры способны быстро решать задачи, на которые даже у суперкомпьютеров уйдут тысячелетия.
— Но есть нюанс. Пока квантовый компьютер дает выгоду только для определенного круга задач. Сейчас они и строятся под такие задачи. Поиск дающих выгоду квантовых алгоритмов — это сама по себе отдельная дисциплина, — рассказывает Дмитрий Могилевцев. — Бум квантовых компьютеров начался с того, что американец Питер Шор предложил с их помощью решать очень важную с практической точки зрения задачу факторизации. Она имеет огромное значение в криптографии.

Перемножить целые числа — это просто, а вот узнать, на какие простые множители разлагается число — крайне трудная задача для классического компьютера. 15 факторизуется на простые числа 3 и 5. Но что если число очень большое и состоит из тысяч цифр?
В теории на классическом компьютере такую задачу разрешить можно, однако на практике это потребует много времени. Увеличивается число — временны́е затраты возрастают по экспоненте и быстро выходят на времена, сравнимые с возрастом Вселенной. А алгоритм Шора, используя возможности квантовых компьютеров, способен произвести факторизацию за время, не намного превосходящее время умножения целых чисел.
Например, современный суперкомпьютер, позволяющий делать более десяти в пятнадцатой степени операций в секунду, разложил бы число с пятьюстами знаками за 5 млрд лет. Квантовый компьютер со скоростью всего миллион операций в секунду решил бы ту же задачу за 18 секунд.
Так как факторизация лежит в основе всей современной криптографии, изобретение эффективных квантовых компьютеров поставит под угрозу большинство активно используемых ныне методов шифрования данных. Ведь вся информация, которая нынче передается через сеть, подвергается шифрованию — банковские транзакции, секретная переписка в соцсетях и прочее. Квантовый компьютер сможет подобрать код для расшифровки этих данных в мгновение ока. И тогда не останется ничего тайного.

— Правда, надолго ли — это еще вопрос. Уже сейчас ведутся работы над постквантовым шифрованием, устойчивым к подобному взлому. Хотя эффективность таких систем криптографии пока еще много хуже традиционных.
А еще квантовые компьютеры могут быть очень полезными для моделирования динамики сложных квантовых систем. Именно в этом еще в начале 80-х годов прошлого века видел их выгоду знаменитый физик, лауреат Нобелевской премии Ричард Фейнман. Кстати, сама идея квантовых вычислений предложена известным советским математиком Юрием Маниным в 1980 году.
Квантовые вычисления – что это такое
Идея квантовых вычислений была впервые предложена в начале 1980-х годов Ричардом Фейнманом и Юрием Маниным. Фейнман и Манин считали, что квантовый компьютер может моделировать данные способами, которые недоступны ламповым и транзисторным компьютерам. Лишь в конце 1990-х годов исследователи создали первые подобия квантовых компьютеров.
Квантовые вычисления используют принципы квантовой механики, такие как суперпозиция и запутывание, для выполнения вычислений. Квантовая механика – это раздел физики, который изучает законы взаимодействия на уровень мельчайших частиц энергии.
Основной блок обработки квантовых вычислений – это квантовые биты или кубиты. Кубиты образуются в квантовом компьютере с использованием квантово-механических свойств отдельных атомов, субатомных частиц или сверхпроводящих электрических цепей.
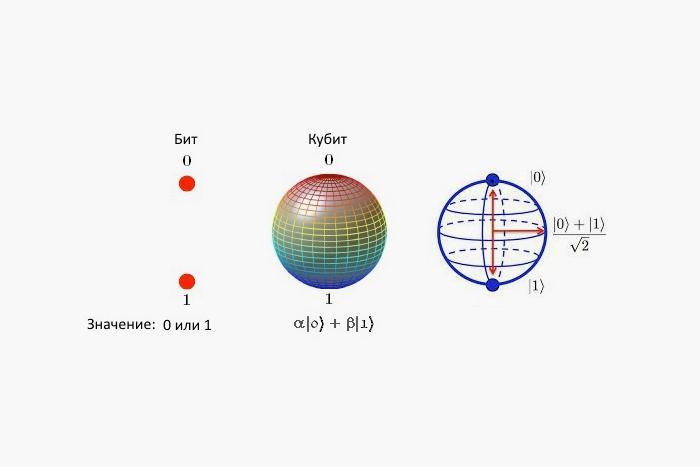
Кубиты похожи на биты, используемые в стандартном компьютере, тем, что кубиты могут находиться в квантовом состоянии 1 или 0. Но, кубиты отличаются тем, что они также могут находиться в суперпозиции состояния 1 и 0, то есть кубиты могут представлять как 1, так и 0 одновременно.
Когда кубиты находятся в суперпозиции, два квантовых состояния складываются вместе и приводят к другому квантовому состоянию. Суперпозиция означает, что несколько вычислений обрабатывается одновременно. Таким образом, два кубита могут представлять четыре числа одновременно. Обычные компьютеры обрабатывают биты только в одном из двух возможных состояний – 1 или 0, а вычисления обрабатываются по очереди.
Квантовые компьютеры также используют эффект запутывания для обработки кубитов. Когда кубит запутан, это означает, что состояние одного кубита влияет на состояние другого кубита, независимо от расстояния.
Как работает квантовый компьютер
Квантовые компьютеры для вычислений используют такие свойства квантовых систем, как суперпозиция и запутанность. В суперпозиции квантовые частицы представляют собой комбинацию всех возможных состояний, пока не произойдет их наблюдение и измерение. Запутанные кубиты образуют единую систему и влияют друг на друга. Измерив состояние одного кубита, возможно сделать вывод об остальных. С увеличением числа запутанных кубитов экспоненциально растет способность квантовых компьютеров обрабатывать информацию.
Базовым элементом, выполняющим логические операции в классическом компьютере, является вентиль. Для работы квантового компьютера используются квантовые вентили, собранные из кубитов. Они бывают однокубитные и двухкубитные. Также существуют универсальные наборы вентилей, с помощью которых можно выполнить любое квантовое вычисление
Кроме того, квантовые компьютеры не могут работать со стандартным софтом вроде Windows. Для них требуется своя операционная система и приложения. Некоторые технологические гиганты уже предлагают организациям опцию квантовых вычислений в облаке. Облачные квантовые вычисления обеспечивают прямой доступ к эмуляторам, симуляторам и квантовым процессорам.
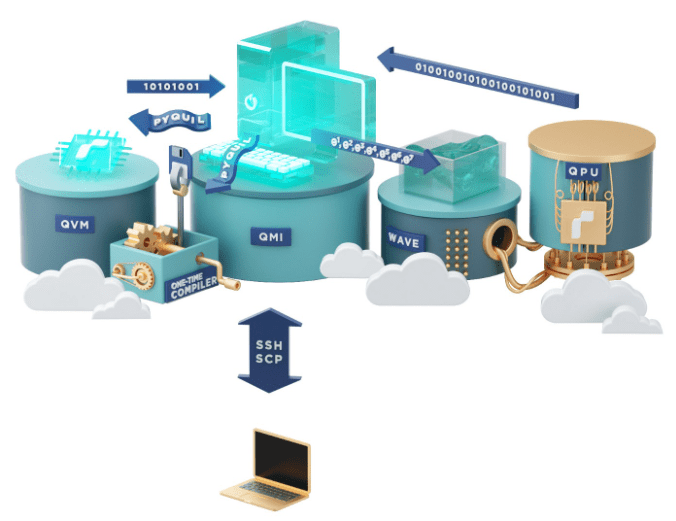
Поставщики также предоставляют платформы разработки и документацию для языков и инструментов вычислений. IBM уже представила программную платформу для квантовых вычислений с открытым исходным кодом под названием Qiskit. А Microsoft выпустила инструмент бесплатного разработчика вычислительной техники на языке Q# и симулятор квантовых вычислений. Над разработкой ПО для квантовых компьютеров работают также 1QBit, Cambridge Quantum Computing, QSimulate, Rahko, Zapata и другие компании.
Для работы квантовых компьютеров требуются квантовые алгоритмы. Из наиболее известных квантовых алгоритмов можно выделить три:
-
(разложения числа на простые множители) (решение задачи перебора, быстрый поиск в неупорядоченной базе данных) (ответ на вопрос, постоянная или сбалансированная функция)
Квантовый компьютер работает на вероятностном принципе. Его результатом работы является распределение вероятностей возможных ответов, наиболее вероятный ответ обычно является лучшим решением.
Квантовые кубиты в физической реализации бывают нескольких типов: сверхпроводниковые, зарядовые, ионные ловушки, квантовые точки и другие.
Настоящий уровень развития технологий позволяет создать большое количество кубитов, сложность возникает с устойчивостью такой системы. Как и все квантовые системы, кубиты легко теряют заданное квантовое состояние при взаимодействии с окружением (происходит их декогеренция). При этом в работе квантового компьютера растет количество ошибок вычислений. Чтобы обеспечить ее устойчивость при проведении вычислений, требуется оградить систему от любого фонового шума, например, в случае сверхпроводниковых систем, охлаждая их до температур, близких к нулю по Кельвину (-273,1 °C). Разработчики используют сверхтекучие жидкости, чтобы добиться такого охлаждения.

Как объяснил Руслан Юнусов, исторически сверхпроводники считались наиболее перспективным направлением благодаря хорошей масштабируемости, стабильности во времени, контроле параметров и относительной легкости управления ими. Именно на этой платформе построены квантовые компьютеры IBM, Google и Rigetti. Однако, по его словам, в последнее время все большую популярность приобретают альтернативные квантовые платформы: ионы, демонстрирующие высочайшие на сегодняшний день показатели стабильности и точности операций (Honeywell, IonQ), и фотоны, преимуществами которых являются малый размер фотонного процессора и возможность работы при комнатных температурах (Xanadu, PsiQuantum, Quix).
Кроме того, развиваются новые концепции: системы на поляритонах или магнонах, системы бозе-эйнштейновских конденсатов, когерентные машины Изинга, когерентные CMOS-архитектуры. Так, в поляритонной архитектуре битом служит поляритон — квазичастица, сочетающая свойства света и вещества. Теоретически, поляритонный квантовый компьютер сможет работать при комнатной температуре, что снизит его стоимость и упростит изготовление. В настоящее время изучением поляритонных структур занимается Сколтех.
Китайский квантовый компьютер
В 2020 году достигнуть квантового превосходства попытались китайские ученые. Для этого они разработали компьютер, предназначенный для решения задачи по сэмплированию бозонов. Если говорить очень коротко, то системе нужно было рассчитать прохождение частиц света (фотонов) через оптический прибор. Эта задача была сформулирована несколько лет назад, но математическую формулу для ее решения создать попросту невозможно. По словам авторов научной работы, суперкомпьютеру TaihuLight для решения этой задачи потребовалось бы около 2,5 миллиардов лет. Но квантовый компьютер справился с задачей всего за 200 секунд.

Один из самых мощных компьютеров в мире — Sunway TaihuLight
Решение стало возможным благодаря одной хитрости. Так как в задаче речь идет о частицах света, вместо кубитов в компьютере использовались такие же фотоны. Таким образом ученые упростили задачу прямо «на уровне железа». Получается, что исследователям действительно удалось достичь квантового превосходства. Но и на это раз без критики не обошлось. Дело в том, что созданное для решение задачи устройство можно назвать компьютером лишь с большой натяжкой. В нем используются квантовые вычисления при помощи кубитов, но его нельзя программировать. То есть, на данный момент такой компьютер нельзя использовать для решения других задач. Но факт того, что квантовое преимущество достигнуто, уже есть.
Однако, с течением времени программируемая система на основе квантов все равно наверняка будет создана. Когда это случится, технологии станут развиваться с молниеносной скоростью. Например, человечество сможет быстро изобретать лекарства от опасных заболеваний и даже узнавать тайны Вселенной. Подробнее о том, как работает квантовый компьютер, можно узнать из этого видео.
История идеи
Идею квантовых вычислительных устройств впервые высказал в 1980 году советский математик Юрий Манин. В книге «Вычислимое и невычислимое», рассуждая о сложности процесса считывания и записи биологической информации с молекул ДНК, он заметил, что для моделирования этого процесса могли бы подойти квантовые устройства. Здесь же Манин указал указал на главное их преимущество — рост числа состояний таких устройств идет по степенному закону:

Годом позже, в мае 1981 года, идею квантового компьютера сформулировал физик и нобелевский лауреат Ричард Фейнман в докладе, посвященном возможности моделирования физических процессов.
Ученый подчеркнул, что все явления подчиняются квантовым законам (а классическая физика — только приближение). Если поведение одиночного квантового объекта достаточно легко поддается моделированию с помощью компьютера, то нарастание количества элементов ведет к экспоненциальному росту сложности вычислений.
Из этого следовало два выхода, говорил Фейнман: первый — признать, что квантовые системы не поддаются моделированию с помощью компьютеров, и второй — построить вычислительную машину из квантовых элементов, подчиняющихся тем же квантовым законам, что и моделируемая система.
В своем докладе Фейнман впервые сформулировал понятие квантового симулятора — квантовой системы, воспроизводящей поведение какой-то другой квантовой системы, а также универсального квантового компьютера — такой квантовой системы, которую можно перенастроить (перепрограммировать) так, чтобы она была способна моделировать поведение многих других систем.
Наконец, Фейнман также впервые описал пример работы системы из кубитов, созданных из фотонов с определенной поляризацией.

Работа одного из элементов квантового компьютера в представлении Фейнмана
В 1985 году Дэвид Дойч из Оксфордского университета разработал теорию универсального квантового компьютера как квантовой машины Тьюринга.
Однако первый в мире квантовый компьютер мог появиться намного раньше, еще до статей Манина и Фейнмана, в 1950-е годы. Тогда японский ученый Гото Эйичи экспериментировал с низкотемпературной электроникой для разработки миниатюрного магнитно-управляемого бита, то есть системы, способной находиться в двух состояниях и служить, как и обычный полупроводниковый транзистор, основным элементом компьютера.
Эйичи назвал свой бит параметроном, и его первый прототип был создан в 1958 году в Токийском университете. Ниже представлен схематический чертеж оригинального устройства Гото.

Гото Эйичи и его команда повысить энергетический барьер между двумя состояниями битов, чтобы их гарантированно можно было различить. Иначе говоря, японские ученые хотели, чтобы устройство ни в коем случае не оказывалось в бистабильном состоянии, то есть в состоянии квантовой суперпозиции.
Такое состояние рассматривалось ими как нечто, вызывающее неуправляемый и нежелательный шум, в то время как квантовые эффекты могли дать им принципиально новый метод вычислений. Если бы не стремление японских специалистов к избавлению от ошибок, квантовые симуляторы, возможно, появились бы на полвека раньше.
СОДЕРЖАНИЕ
По основной теореме арифметики каждое натуральное число имеет единственное разложение на простые множители . (По соглашению 1 — это пустой продукт .) Проверить , является ли целое число простым, можно за полиномиальное время , например, с помощью теста простоты AKS . Однако, если они составные, тесты на полиномиальное время не дают понимания того, как получить коэффициенты.
Среди b- битных чисел сложнее всего разложить на множители с использованием существующих алгоритмов те, которые являются произведением двух простых чисел одинакового размера. По этой причине эти целые числа используются в криптографических приложениях. Самым крупным из таких полупростых чисел, который когда-либо учитывался, был RSA-250 , 829-битное число с 250 десятичными знаками, в феврале 2020 года. Общее время вычислений составило примерно 2700 ядерно-лет вычислений с использованием Intel Xeon Gold 6130 на частоте 2,1 ГГц. Как и все недавние записи факторизации, эта факторизация была завершена высокооптимизированной реализацией сита общего числового поля, запущенного на сотнях машин.
Сложность и сложность
Не было опубликовано ни одного алгоритма , который мог бы разложить все целые числа на множители за полиномиальное время , то есть разложить b- битное число n на множители за время O ( b k ) для некоторой константы k . Ни существование, ни отсутствие таких алгоритмов не было доказано, но обычно предполагается, что их не существует и, следовательно, проблема не в классе P. Проблема явно в классе NP, но обычно предполагается, что она не является NP-полным , хотя это не было доказано.
Есть опубликованные алгоритмы, которые быстрее, чем O ((1 + ε ) b ) для всех положительных ε , то есть субэкспоненциальные . По состоянию на 2021-03-12 алгоритм с наилучшим теоретическим асимптотическим временем работы — это решето общего числового поля ( GNFS ), впервые опубликованное в 1993 году, работающее на b- битном числе n во времени:
Для современных компьютеров GNFS — лучший опубликованный алгоритм для больших n (более 400 бит). Для квантового компьютера , однако, Питер Шор обнаружил алгоритм в 1994 году , который решает его в полиномиальное время. Это будет иметь серьезные последствия для криптографии, если квантовые вычисления станут масштабируемыми. Алгоритм Шора занимает только O ( b 3 ) времени и O ( b ) пространства на входных b- битных числах. В 2001 году алгоритм Шора был впервые реализован с использованием методов ЯМР на молекулах, содержащих 7 кубитов.
Неизвестно, какие именно классы сложности содержат вариант решения задачи целочисленной факторизации (то есть: имеет ли n множитель меньше k ?). Известно, что он присутствует как в NP, так и в co-NP , что означает, что оба ответа «да» и «нет» могут быть проверены за полиномиальное время. Ответ «да» может быть подтвержден факторизацией n = d ( n / d ) с d ≤ k . Ответ «нет» может быть подтвержден демонстрацией факторизации n на различные простые числа, все больше k ; можно проверить их простоту с помощью теста на простоту AKS , а затем умножить их, чтобы получить n . Основная теорема арифметики гарантирует , что существует только одна возможная строка увеличивающихся простых чисел , которые будут приняты, что свидетельствует о том , что проблема в обоих UP и со-UP. Известно, что он входит в BQP из-за алгоритма Шора.
Предполагается, что проблема находится вне всех трех классов сложности P, NP-полной и co-NP-полной . Таким образом, он является кандидатом в NP-средний класс сложности. Если бы можно было доказать, что он является либо NP-полным, либо co-NP-полным, это означало бы NP = co-NP, очень неожиданный результат, и поэтому многие подозревают, что целочисленная факторизация находится за пределами обоих этих классов. Многие люди пытались найти для него классические алгоритмы с полиномиальным временем, но потерпели неудачу, поэтому многие подозревают, что он находится за пределами P.
Напротив, проблема решения «Является ли n составным числом?» (или, что эквивалентно: «Является ли n простым числом?») оказывается намного проще, чем проблема определения множителей n . Задача составного / простого числа может быть решена за полиномиальное время (в количестве b цифр n ) с помощью теста на простоту AKS . Кроме того, существует несколько вероятностных алгоритмов, которые могут очень быстро проверить простоту на практике, если кто-то готов допустить исчезающе малую вероятность ошибки. Простота проверки простоты является важной частью алгоритма RSA , поскольку для начала необходимо найти большие простые числа.
Биты — убиты
— А вы можете объяснить для профана-гуманитария — в чем главное отличие квантового компьютера от обычного. На пальцах, что называется. Я постараюсь напрячь мозг.
— Давайте попробуем (улыбается). В обычном компьютере вся информация зашифрована в битах. 1 бит — 1 единица информации. А биты, в свою очередь, состоят из одних только нулей и единичек. Все, что содержится в вашем планшете, смартфоне, ноутбуке, тексты, фото, картинки — все зашифровано с помощью единиц и нулей. Которые — внимание! — могут составлять одномоментно лишь одно состояние, пусть даже и сложное. Для 10 битов, например, 1001101010.
В КК вся информация зашифрована в кубитах (к слову «биты» просто добавлена приставка «ку» — от английского слова quantum, что означает «квант»). В роли этих кубитов могут выступать или атомы редкоземельных металлов итербия, тулия, или частицы света фотоны, или ионы — заряженные атомы, «потерявшие» или, наоборот, «приобретшие» один или несколько электронов. Или просто электрические цепи в сверхпроводниках.
Все эти атомы или фотоны в квантовом мире могут быть там и тут одновременно. И единицей, и нулем. Это называется суперпозицией. Обычный компьютер оперирует только одним состоянием. А квантовый. У него возможных состояний 2 в той степени, сколько заложено в нем кубитов. Если кубитов 10, то он одновременно в 1024 состояниях, а если всего лишь 300, то 2 в 300-й степени — это больше, чем атомов во всей Вселенной, можете себе такое представить? КК «соображает» сразу на всех уровнях. Параллельно. Поэтому он всегда будет на голову выше любого обычного компьютера, пусть даже и с приставкой «супер». Можно и дальше углубляться в странные законы квантового мира, например, для КК нужна еще и квантовая запутанность. Слышали про такое?
— Ну, кто ж не знает про квантовую запутанность. Кстати, не так давно ученые из Шанхайского университета представили КК «Цзючжан», который, как они заявили, является на сегодняшний день самым мощным квантовым компьютером. Во время демонстрации он всего за несколько минут решил задачу по отбору проб гауссовских бозонов. Это я цитирую информационное агентство, не пугайтесь моей грамотности. С подобной задачей самый мощный современный суперкомпьютер справился бы только за 2,5 миллиарда лет. Получается — КК уже создан, гонка завершилась?
— Что вы, только начинается. Китайский продукт — это не полноценный, не универсальный квантовый компьютер. Он так называемый симулятор, который предназначен лишь для демонстрации «квантового превосходства». Другими словами, «Цзючжан» делает на публике то, чего никогда не сможет сделать обычный суперкомпьютер, пусть даже с миллионами ядер. В прошлом году, кстати, Google представила свой прототип КК — Sycamore. Китайские ученые сообщили, что скорость вычислений их КК в 10 миллиардов раз выше, чем гугловского. Но последний уже программируется, то есть может решать разные задачи, а китайский нет. Что, конечно, никак не умаляет заслуг шанхайских ученых. К слову, один из руководителей программы, профессор Лю Чаоян сказал, что создание КК — это гонка не между странами, а между человечеством и природой. Очень точное замечание.












