
Речь каждого человека является неповторимой и имеет целый ряд индивидуальных особенностей. Голос человека столь же уникален, как строение сетчатки глаза или отпечатки пальцев. По голосу человека можно судить о его характере. Также известно, что общее впечатление о человеке наполовину зависит от мимики, на треть — от голоса и только лишь на малую часть — от того, что этот человек говорит.
Индивидуальные особенности голоса говорящего можно использовать не только в задачах идентификации, но и для определения настроения человека, борьбы с телефонными мошенниками и т.д. Круг прикладных задач этим не ограничивается. Так, например, существует зависимость между частотами среднего тона и гендерной принадлежностью — мужчины говорят на частоте 85-200Hz, а женщины — 160-340Hz. Таким образом, можно придумать множество прикладных сценариев, где выделение индивидуальных особенностей говорящего будет необходимо.
Обращаясь к проблеме распознавания речи, прежде всего, необходимо определить, что именно нужно сравнивать. Непосредственное сравнение звуковых сигналов во временной области является процессом долгим и неэффективным. Спектрограммы – более быстрый способ, но не намного эффективнее. Поиски максимально рационального представления приводят к кепстральным коэффициентам, которые часто используются в качестве характеристики речевых сигналов.
Как только слово выделяется из потока входных данных, начинается этап процесса выделение необходимых характеристик. В этом случае могут применяться различные методики, например методика нахождения мел-кепстральных коэффициентов или коэффициентов линейного предсказания. Основная задача на данном этапе — выделение неких параметров сигнала, причем число этих параметров должно быть минимально, чтобы ускорить сравнение с наборами параметров из библиотеки, и в то же время данные параметры должны быть такими, чтобы по ним можно было достаточно точно определить конкретное слово.
Таким образом, можно сделать вывод, что в задачах, связанных с обработкой речи, сигнал не подается напрямую в систему, а представляет собой набор компактных характеристик для наилучшего процесса их манипуляции. Более конкретно, если обратиться к рисунку 1, можно заметить, что для эффективного представления сигнала этап выделения ключевых характеристик речи присутствует как на фазе обучения, так и на фазе выполнения.
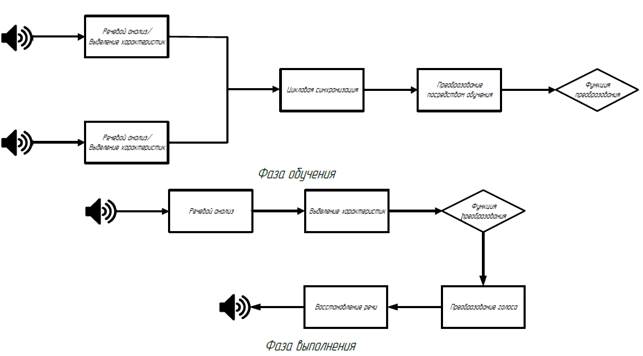
Рисунок 1 – Типовая система преобразования голоса
Обработка спектральных характеристик речи является следствием управления просодией. Однако существует множество представлений спектральных характеристик. Для процесса статистического параметрического моделирования, характеристики должны отвечать следующим требованиям [6]:
- качественно передавать индивидуальные особенности речи диктора как личности;
- в достаточной степени соответствовать спектральной огибающей и обладать способностью в нее преобразовываться;
- обладать качественными свойствами интерполяции и возможностью гибкой модификации.
Спектральные характеристики являются многомерными, поэтому занимают значительную часть памяти при работе с большими объемами данных. Поэтому необходимо прибегнуть к наиболее эффективному одномерному представлению спектра, который может быть использован в дальнейшем на практике [7]. Поиски наиболее рационального представления приводят к кепстральным коэффициентам, которые часто используются в качестве характеристики речевых сигналов.
В процессе эволюции живые существа, обладающие сенсорными системами, развивались по принципу: «различать, для того чтобы выжить». Слуховой аппарат человека как сенсорный анализатор имеет способность обеспечивать различение звуков по их частотному составу. Однако реакция на звуковой стимул должна быть быстрой, а значит, обработка сигналов в ухе и нервной системе должна выполняться за небольшое время. Требования высокой частотной и временной различительной способности анализатора противоречивы, но результатом эволюции было оптимальное сочетание этих показателей.
Органы слуха человека обладают свойством частотного маскирования, где под маскированием понимают ситуацию, при которой нормально слышимый звук накрывается другим громким звуком с близкой частотой. Данная характеристика зависит от частоты сигнала и варьируется от 100 Гц для низких слышимых частот до более 4000 Гц для высоких частот. Следовательно, область слышимых частот можно разделить на несколько критических полос (принято деление на 24 критические полосы), которые обозначают падение чувствительности уха для более высоких частот.
Можно считать критические полосы еще одной характеристикой звука, подобной его частоте. Однако, в отличие от частоты, которая абсолютна и не зависит от органов слуха, критические полосы определяются в соответствии со слуховым восприятием. В итоге они образуют некоторые меры восприятия частот, для которых введены единицы измерения — барк и мел.
Использование кепстрального анализа широко распространено в задачах, связанных с обработкой речи. Большинство современных автоматических систем синтеза и распознавания речи сосредотачивают усилия на извлечении частотной характеристики речевого тракта человека, отбрасывая при этом характеристики сигнала возбуждения. Это объяснено тем, что коэффициенты первой модели обеспечивают лучшую разделимость звуков. Для отделения сигнала возбуждения от сигнала речевого тракта прибегают к кепстральному анализу.
Модель кепстральных коэффициентов, как для минимумов, так и для максимумов оптимально соответствует спектральной огибающей — важной характеристике синтеза речи. Частный случай кепстральных коэффициентов — Мел-кепстральные коэффициенты, представляющие собой спектральную огибающую с коэффициентами, расположенными друг от друга на расстоянии по шкале Мела, которые сосредоточены на частотах, имеющих большое значение для человеческой речи и слуха [1]. Их использование в задаче описания характеристик фонемы обусловлено прежде всего удобством практического применения.
Мел-кепстральные коэффициенты обладают повышенной помехоустойчивостью и позволяют принимать достоверные решения на относительно коротких интервалах анализа речи. Основной идеей метода Мел-кепстральных коэффициентов является максимальное приближение информации поступающей на слуховой анализатор мозга человека. Признаки, построенные на основе Мел-кепстральных коэффициентов, учитывают психоакустические принципы восприятия речи, поскольку используют мел-шкалу, связанную с критическими полосами слуха.
Необходимо понимать значение понятий мела и кепстра. Мел — это единица высоты звука, которая основана на восприятии этого звука органами слуха человека или, другими словами, своеобразное представление энергии спектра сигнала, которое обычно является вектором из тринадцати вещественных чисел. Кепстр (cepstrum) — в свою очередь, это результат дискретного косинусного преобразования от логарифма амплитудного спектра сигнала.
Для того чтобы найти энергию сигнала, вектор спектра сигнала перемножается с функцией окна, в результате чего получается вектор коэффициентов. Если их возвести в квадрат, представить в виде логарифма и получить из них кепстральные коэффициенты, то получаются искомые Мел-коэффициенты. Кепстральные коэффициенты можно получить как с помощью Фурье-преобразования, так и с помощью дискретного косинусоидального преобразования [6]. Дискретное косинусоидальное преобразование применяется для получения кепстральных коэффициентов, оно сжимает полученные результаты, повышает вклад первых коэффициентов и понижает вклад последних.
Плюсы использования кепстральных коэффициентов заключаются в следующем:
· Используется спектр сигнала (то есть разложение по базису ортогональных косинусоидальных или синусоидальных функций), что позволяет учитывать волновую «природу» сигнала при дальнейшем анализе;
· Спектр проецируется на специальную Мел-шкалу, позволяя выделить наиболее значимые для восприятия человеком частоты;
· Количество вычисляемых коэффициентов может быть ограничено любым значением (например, 12), что позволяет «сжать» фрейм и, как следствие, количество обрабатываемой информации;
В работе [5] был предложен унифицированный подход к спектральному анализу речи, позволяющий вычислять различные наборы параметров. В эти параметры, помимо прочих, входят линейное предсказание и Мел-кепстральный анализ. За счет изменения параметров α и γ, есть возможность выбирать между доступными параметрами.
Кепстр 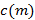 действительной последовательности
действительной последовательности 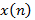 определяется как обратное преобразование Фурье логарифмического спектра, в то время как Мел-обобщенные кепстральные коэффициенты
определяется как обратное преобразование Фурье логарифмического спектра, в то время как Мел-обобщенные кепстральные коэффициенты 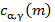 определяются как обратное преобразование Фурье обобщенного логарифмического спектра, рассчитанное по деформированной частотной шкале
определяются как обратное преобразование Фурье обобщенного логарифмического спектра, рассчитанное по деформированной частотной шкале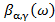 :
:
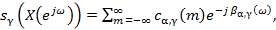 (1)
(1)
где 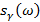 — обобщенная логарифмическая функция и
— обобщенная логарифмическая функция и 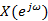 – преобразование Фурье для
– преобразование Фурье для 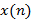 . Обобщенная логарифмическая функция определяется следующим образом:
. Обобщенная логарифмическая функция определяется следующим образом:
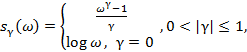 (2)
(2)
а деформированная шкала частот 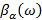 рассчитывается как фазовая характеристика пропускающей системы [2]:
рассчитывается как фазовая характеристика пропускающей системы [2]:
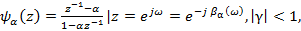 (3)
(3)
где 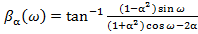 . (4)
. (4)
В работе [4] допускается, что спектр речи 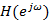 может быть смоделирован
может быть смоделирован 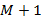 Мел-обобщенными кепстральными коэффициентами следующим образом:
Мел-обобщенными кепстральными коэффициентами следующим образом:
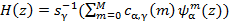 (5)
(5)
Выбрав 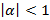 и
и 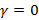 , можно получить Мел-кепстральную функцию (MCEP):
, можно получить Мел-кепстральную функцию (MCEP):
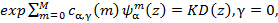 (6)
(6)
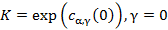 , (7)
, (7)
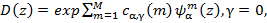 (8)
(8)
а 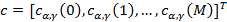 – вектор Мел-кепстральных коэффициентов со специальным коэффициентом
– вектор Мел-кепстральных коэффициентов со специальным коэффициентом 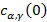 , обычно называемым энергетической компонентой, так как он соответствует средней логарифмической мощности кадра [4]. Вычислительная сложность алгоритма кепстрального преобразования при использовании быстрого преобразования Фурье приближенно равна
, обычно называемым энергетической компонентой, так как он соответствует средней логарифмической мощности кадра [4]. Вычислительная сложность алгоритма кепстрального преобразования при использовании быстрого преобразования Фурье приближенно равна 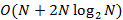 .
.
Мел-обобщенные кепстральные коэффициенты широко используются в проектах, связанных с преобразования голоса, позволяют достигать лучшей производительности по сравнению с другими вариантами и обеспечивают качественное квантование, интерполяцию и представление формантной структуры. Их использование также позволяет избегать создания артефактов в процессе синтеза речи[3].
Применение распределений мел-частотных кепстральных коэффициентов для голосовой идентификации личности Текст научной статьи по специальности « Компьютерные и информационные науки»
Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Заковряшин Алексей Сергеевич, Малинин Петр Владимирович, Лепендин Андрей Александрович
Работа посвящена развитию методов распознавания личности на основе голосовых данных. Предложен новый подход к формированию векторов признаков при предварительной обработке голосовых образцов, основанный на построении гистограмм частотных распределений мел-частотных кепстраль-ных коэффициентов. Отличительной особенностью является независимость полученного вектора от длины исходного голосового образца, его относительно малый размер и учет в нем разброса индивидуальных характеристик голосового тракта идентифицируемого субъекта. Разработан программный модуль идентификации личности по голосу на основе предложенного подхода и метода опорных векторов. Программный модуль реализован на языке МайаЬ с использованием функций пакета ^нсеЬох. Проведено сравнение с традиционно используемыми при решении задачи идентификации дикторов векторами признаков . Тестовые испытания разработанного модуля показали, что предложенный подход к предварительной обработке голосовых данных позволяет достичь относительно низкого значения вероятностей ошибок первого и второго рода и может использоваться при построении эффективных систем речевой идентификации.
Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Заковряшин Алексей Сергеевич, Малинин Петр Владимирович, Лепендин Андрей Александрович
Speaker Recognition Using Mel-Frequency Cepstral Coefficient Distributions
This paper is devoted to the development of feature extraction methods for speaker recognition . A new approach based on histograms of mel-frequency cepstral coefficient (MFCC) distributions to calculate feature vectors for voice samples is proposed. The resulting vectors appear to be independent of original voice sample length and have relatively small sizes. They incorporate the spread of unique vocal tract related characteristics which can be used as distinctive features for recognition. This approach of voice recognition is implemented in a software module developed for MATLAB environment. A support vector machine method and Voicebox speech processing toolbox for MATLAB are utilized. Results of the developed module test runs are obtained and reported. A comparison of test results with results of traditionally used feature vector based techniques of speaker recognition shows relatively low rates of false acceptance and false match for the proposed approach. Feature vectors based on MFCC distributions can be effectively used in real world voice recognition systems.
Текст научной работы на тему «Применение распределений мел-частотных кепстральных коэффициентов для голосовой идентификации личности»
УДК 004.056+ 004.852
А. С. Заковряшин, П. В. Малинин, А. А. Лепендин
Применение распределений мел-частотных кепстральных коэффициентов для голосовой идентификации личности
A. S. Zakovryashin, P. V. Malinin, A. A. Lependin
Speaker Recognition Using Mel-Frequency Cepstral Coefficient Distributions
Работа посвящена развитию методов распознавания личности на основе голосовых данных. Предложен новый подход к формированию векторов признаков при предварительной обработке голосовых образцов, основанный на построении гистограмм частотных распределений мел-частотных кепстральных коэффициентов. Отличительной особенностью является независимость полученного вектора от длины исходного голосового образца, его относительно малый размер и учет в нем разброса индивидуальных характеристик голосового тракта идентифицируемого субъекта. Разработан программный модуль идентификации личности по голосу на основе предложенного подхода и метода опорных векторов. Программный модуль реализован на языке МайаЬ с использованием функций пакета ^нсеЬох. Проведено сравнение с традиционно используемыми при решении задачи идентификации дикторов векторами признаков. Тестовые испытания разработанного модуля показали, что предложенный подход к предварительной обработке голосовых данных позволяет достичь относительно низкого значения вероятностей ошибок первого и второго рода и может использоваться при построении эффективных систем речевой идентификации.
Ключевые слова: голосовая идентификация личности, вектор признаков, мел-частотные кепстральные коэффициенты, распределение частот.
This paper is devoted to the development of feature extraction methods for speaker recognition. A new approach based on histograms of mel-frequency cepstral coefficient (MFCC) distributions to calculate feature vectors for voice samples is proposed. The resulting vectors appear to be independent of original voice sample length and have relatively small sizes. They incorporate the spread of unique vocal tract related characteristics which can be used as distinctive features for recognition. This approach of voice recognition is implemented in a software module developed for MATLAB environment. A support vector machine method and Voicebox speech processing toolbox for MATLAB are utilized. Results of the developed module test runs are obtained and reported. A comparison of test results with results of traditionally used feature vector based techniques of speaker recognition shows relatively low rates of false acceptance and false match for the proposed approach. Feature vectors based on MFCC distributions can be effectively used in real world voice recognition systems.
Key words: speaker recognition, feature vector, mel-frequency cepstrum coefficients, frequency distribution.
Введение. Задача верификации диктора по голосовым данным в настоящее время находит широкое применение при построении безопасных информационных систем. Как правило, ее решение основывается на выявлении индивидуальных акустических характеристик пользователей, которые бы позволили эффективно и точно проводить сравнение образцов голоса, предъявляемых при попытке доступа и сохраняемых в специализированной базе данных.
Как и любой другой биометрический подход, голосовая идентификация не является абсолютно надежной. На ее качество влияют расположение диктора относительно микрофона, состояние его здоровья (на-
личие или отсутствие хрипа в голосе), характеристики регистрирующего тракта, особенности реализации алгоритмов предварительной обработки сигнала и получения вектора признаков, его характеризующего, применяемый алгоритм идентификации. Таким образом, несмотря на активное развитие систем голосовой идентификации, имеется необходимость в их постепенном совершенствовании.
В настоящей работе предлагается новый подход к формированию вектора признаков, описывающего индивидуальные характеристики голоса диктора. Он основан на применении уже хорошо зарекомендовавшего способа выделения полезной информации об акустиче-
ском сигнале, основанном на вычислении мел-частотных кепстральных коэффициентов (MFCC-Mel Frequiency Cepstral Coefficients) и построении их распределений для фраз произвольной длины. Отличительной особенностью предлагаемого подхода является независимость полученного вектора от длины исходного голосового образца, его относительно малый размер и учет в нем разброса индивидуальных характеристик голосового тракта идентифицируемого субъекта.
1. Получение вектора признаков на основе MFCC. Схема системы идентификации личности на основе голосовых данных реализуется с помощью следующих этапов [1,2]:
1. Уровень обработки сигнала. Выделение признаков, существенных для задачи распознавания и формирование так называемого вектора признаков.
2. Уровень модели. Позволяет путем построения математической модели проводить сопоставление векторов признаков друг с другом и вычислять степени подобия между зарегистрированными признаками и сохраненной моделью.
3. Уровень принятия решений. Проводит принятие конечных решений на основе полученных степеней подобий и, если необходимо, заданных пороговых значений.
К настоящему времени в отрасли сложился типичный алгоритм предварительной обработки акустического сигнала после его записи [3]. Оцифрованный сигнал разбивается на блоки длительностью 25-30 мс (обозначим отсчеты в одном из них x0. xN-1). К каждому подобному блоку применяется весовая функция и затем дискретное преобразование Фурье. Примером весовой функции может служить окно Хэмминга:
w = 0,54 — 0,46 • cos
где N — длина окна, выраженная в отсчетах.
Весовая функция используется для уменьшения искажений в Фурье анализе, вызванных конечностью выборки. Тогда дискретное преобразование Фурье взвешенного сигнала можно записать в виде:
Мел-кепстральные коэффициенты (MFCC) и распознавание речи
Недавно я наткнулся на интересную статью, опубликованную rgen3, в которой описан DTW-алгоритм распознавания речи. В общих чертах, это сравнение речевых последовательностей с применением динамического программирования.
Заинтересовавшись темой, я попробовал применить этот алгоритм на практике, но на этом пути меня поджидало некоторое количество граблей. Прежде всего, что именно нужно сравнивать? Непосредственно звуковые сигналы во временной области — долго и не очень эффективно. Спектрограммы — уже быстрее, но не намного эффективнее. Поиски наиболее рационального представления привели меня к MFCC или Мел-частотным кепстральным коэффициентам, которые часто используются в качестве характеристики речевых сигналов. Здесь я попытаюсь объяснить, что они из себя представляют.
Основные понятия
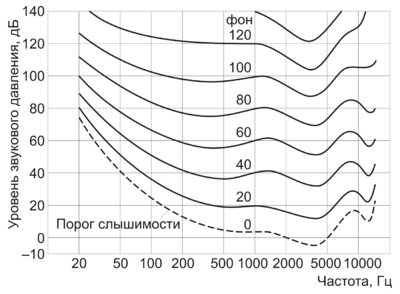
Аналогично, воспринимаемая человеческим слухом высота звука не совсем линейно зависит от его частоты. 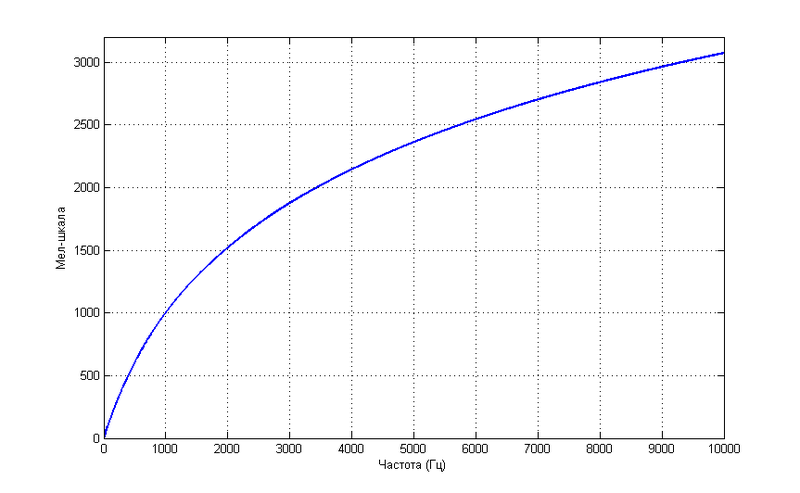
Такая зависимость не претендует на большую точность, но зато описывается простой формулой 
Подобные единицы измерения часто используют при решении задач распознавания, так как они позволяют приблизиться к механизмам человеческого восприятия, которое пока что лидирует среди известных систем распознавания речи.
Нужно немного рассказать и про второе слово в названии – кепстр.
В соответствии с теорией речеобразования речь представляет собой акустическую волну, которая излучается системой органов: легкими, бронхами и трахеей, а затем преобразуется в голосовом тракте. Если предположить, что источники возбуждения и форма голосового тракта относительно независимы, речевой аппарат человека можно представить в виде совокупности генераторов тоновых сигналов и шумов, а также фильтров. Схематично это можно представить так:

1. Генератор импульсной последовательности (тонов)
2. Генератор случайных чисел (шумов)
3. Коэффициенты цифрового фильтра (параметры голосового тракта)
4. Нестационарный цифровой фильтр
Сигнал на выходе фильтра (4) можно представить в виде свертки

где s(t) — изначальный вид акустической волны, а h(t) — характеристика фильтра (зависит от параметров голосового тракта)
В частотной области это выглядит так

Произведение можно прологарифмировать, чтобы получить вместо него сумму

Теперь нам нужно преобразовать эту сумму так, чтобы получить непересекающиеся наборы характеристик исходного сигнала и фильтра. Для этого есть несколько вариантов, например обратное преобразование Фурье даст нам вот что

Также в зависимости от целей можно использовать прямое преобразование Фурье или дискретное косинусное преобразование
Надеюсь, я немного прояснил основные понятия. Осталось понять, как преобразовать речевой сигнал в набор коэффициентов MFCC.
Пример
В качестве подопытной возьмем простую цифру 1, вот ее временное представление 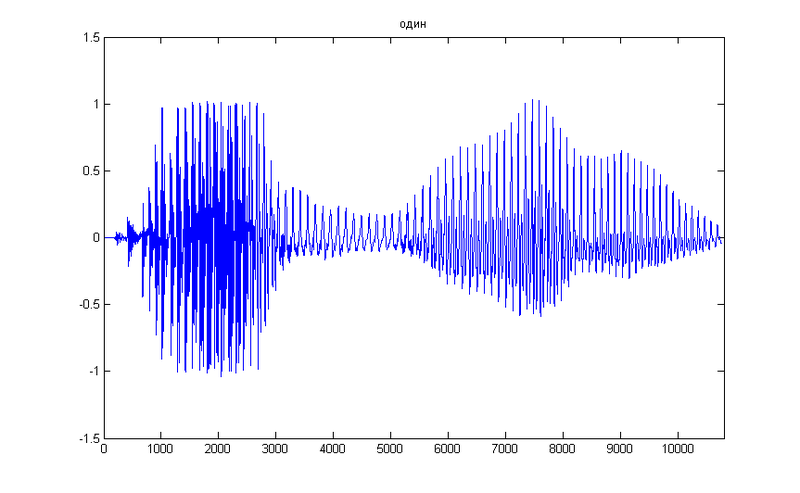
Первым делом нам нужен спектр исходного сигнала, который мы получаем с помощью преобразования Фурье. Для простоты примера, не будем разбивать сигнал на части, поэтому берем спектр по всей временной оси

Теперь начинается самое интересное, полученный спектр нам нужно расположить на мел-шкале. Для этого мы используем окна, равномерно расположенные на мел-оси. 
Если перевести этот график в частотную шкалу, можно увидеть такую картину 
На этом графике заметно, что окна «собираются» в области низких частот, обеспечивая более высокое «разрешение» там, где оно необходимо для распознавания.
Простым перемножением векторов спектра сигнала и оконной функции найдем энергию сигнала, которая попадает в каждое из окон анализа. Мы получили некоторый набор коэффициентов, но это еще не те MFCC, которые мы ищем. Пока их можно было бы назвать Мел-частотными спектральными коэффициентами. Возводим их в квадрат и логарифмируем. Нам осталось только получить из них кепстральные, или «спектр спектра». Для этого мы могли бы еще раз применить преобразование Фурье, но лучше использовать дискретное косинусное преобразование.
В результате получаем последовательность примерно такого вида: 
Заключение
Таким образом мы имеем очень небольшой набор значений, который при распознавании успешно заменяет тысячи отсчетов речевого сигнала. В книгах пишут, что для задачи распознавания слов возможно брать первые 13 из 24 вычисленных коэффициентов, но сколько-нибудь годные результаты в моем случае начинались с 16. В любом случае это намного меньший объем данных, чем спектрограмма или временное представление сигнала.
Для лучшего результата можно разбить исходное слово на отрезки небольшой длительности, и вычислять коэффициенты для каждого из них. Также может помочь «взвешивание» оконных функций. Все зависит от алгоритма распознавания, которому вы скармливаете результат.
Формулы
Не хочется грузить основную часть статьи большим количеством формул, но вдруг они будут кому-то интересны. Поэтому приведу их здесь.
Исходный речевой сигнал запишем в дискретном виде как 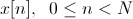
Применяем к нему преобразование Фурье 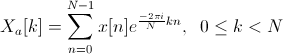
Составляем гребенку фильтров, используя оконную функцию 
Для которой частоты f[m] получаем из равенства 
B(b) — преобразование значения частоты в мел-шкалу, соответственно, 
Вычисляем энергию для каждого окна 
Применяем ДКП 
Мел частотные кепстральные коэффициенты

Человеческий мозг способен распознавать различные визуальные и звуковые образы, в том числе и отличать звучание одного музыкального инструмента от другого, даже на фоне звучания других инструментов. В данной работе рассматривается проблема распознавания звука отдельного музыкального инструмента на основе его спектральных особенностей с применением нейронных сетей.
Задача распознавания музыкальных инструментов востребована при обработке сложных музыкальных сигналов, а именно аудиозаписей музыкальных произведений различных жанров, таких как классическая музыка, эстрадная музыка и другие. Данная задача относится к классу задач Music Information Retrieval (MIR) и может быть использована для аннотирования медиаконтента, сегментации музыкальных сигналов и идентификации музыкальных объектов (нот).
Этой теме посвящено множество исследований, например [2, 3 и 7], но большинство из них используют большое количество признаков для распознавания музыкальных инструментов. Целью данной работы ставится уменьшение количества признаков с получением высокой точности при распознавании отдельно звучащих нот музыкальных инструментов.
Музыкальный звук имеет характерную структуру в спектральном диапазоне (рис. 1.) В его составе есть основной тон, как правило, с наибольшей амплитудой, и сопутствующие гармоники – обертоны, наиболее значимыми являются первые несколько гармоник. Именно эти обертоны определяют тембр звука и соответственно музыкальный инструмент.

Рис. 1. Структура звука музыкального инструмента в спектральном диапазоне [1]
Однако спектр представляет собой большой набор данных, которые нецелесообразно использовать в исходном виде для решения задачи распознавания. В связи с этим необходимо определить значимый набор признаков. В качестве такого набора было решено использовать мел-частотные кепстральные коэффициенты (MFCC). Данные коэффициенты были определены как лучшие признаки для распознавания музыкальных инструментов в работе [5]. Мел-частотные кепстральные коэффициенты представляют собой нелинейный спектр спектра, хорошо аппроксимируют слуховую систему человека, а также успешно используются для решения задач распознавания речи.
Алгоритм вычисления MFCC можно описать следующим образом [4]:
– вычисление оконного преобразования Фурье;
– нелинейное разбиение спектра на n частей c применением мел-шкалы;
– вычисление энергии сигнала для каждого интервала с применением треугольных фильтров (с перекрытием);
– вычисление логарифма энергии сигнала для каждого интервала;
– выполнение дискретного косинусного преобразования.
Для снижения сложности полученного пространства признаков мы использовали метод главных компонент (PCA). Это позволило нам уменьшить корреляцию признаков и удалить наименее значимые из них. Алгоритм вычисления главных компонент может быть описан следующим образом:
– определение матрицы корреляции;
– нахождение собственных значений и соответствующих собственных векторов;
– упорядочивание собственных векторов по соответствующим им собственным значениям (по убыванию);
– нахождение проекций входных данных на собственные векторы;
– отбрасывание последних m проекций.
Первые проекции представляют наиболее значимые компоненты в исходном векторе данных, и, соответственно, последние проекции представляют наименее значимые. Более подробное описание алгоритма может быть найдено в [8].
Для обучения классификатора мы использовали набор маркированных примеров изолированных нот музыкальных инструментов Университета Айовы [9]. Для каждого инструмента были отобраны ноты в их эффективном рабочем диапазоне. Длительность звучания каждой ноты составляла 1–2 секунды. Мы использовали ноты, сыгранные в обычном стиле (деташе) на форте (громко), для обучения классификатора, а для тестирования – ноты, сыгранные на меццо-форте (довольно громко). Данный подход позволил приблизить процесс распознавания музыкальных инструментов к реальному сценарию.
В качестве классификатора мы использовали искусственную нейронную сеть (ИНС) прямого распространения и метод обратного распространения ошибки для обучения сети. Нейронная сеть содержала один скрытый слой. Параметры сети представлены ниже:
– число нейронов в скрытом слое: 24;
– допустимая ошибка классификации: 1 %;
– скорость обучения: 0,05;
– максимальное количество эпох обучения: 250.
Для оценки процесса обучения мы использовали кросс-валидацию. Валидационная часть составляла 30 % от обучающей выборки.
В качестве альтернативы методу обратного распространения ошибки, мы применили нейроэволюционный подход обучения сети, а именно метод Enforced Subpopulations (ESP), предложенный Фаустино Гомесом. Метод адаптирует значения весов ИНС посредством их генетической эволюции. Данный метод использует прямое кодирование и нейронную сеть прямого распространения с одним скрытым слоем. Одна из особенностей данного метода – это использование механизма взрывной мутации на основе распределения Коши для вывода процесса эволюции из локального экстремума. Кратко данный алгоритм может быть описан следующими шагами [6]:
– инициализация – создание h подпопуляций с n нейронами, где h – число нейронов в скрытом слое, n – размер популяции;
– оценка – выбирается случайная комбинация нейронов (по одному из каждой подпопуляции) и формируется нейронная сеть, затем оценивается ее приспособленность. Данная приспособленность добавляется кумулятивно к каждому нейрону этой сети. Оценка продолжается до тех пор, пока каждый нейрон не примет участие как минимум в десяти оценках;
– проверка вырождения – если приспособленность лучшей сети не улучшается в течение b поколений, то выполняется взрывная мутация. Если после двух мутаций не происходит улучшение приспособленности, то выполняется адаптация размера сети;
– рекомбинация – вычисляется средняя приспособленность каждого нейрона, затем они сортируется (в пределах подпопуляции). 25 % лучших нейронов скрещиваются с использованием одноточечного кроссинговера. Для нейронов с низкой приспособленностью выполняется мутация с распределением Коши. В конце происходит выбор лучших n нейроннов.
– этапы оценки-рекомбинации повторяются до тех пор пока не найдена сеть с требуемой приспособленностью (качеством).
Алгоритм распознавания музыкальных инструментов состоит из шести блоков (рис. 2).
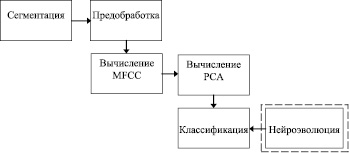
Рис. 2. Схема алгоритма распознавания
Сегментация разбивает сигнал на интервалы по 100 мс, предполагая, что спектр сигнала на этих участках постоянен в статистическом смысле. Предобработка включает увеличение амплитуды частот в верхней части спектра, а также применение оконной функции Хэминга для устранения высоких частот полученных при обрезании сигнала на границах интервала. Предобработка происходит во временнόй области сигнала. Следующими этапами являются вычисление мел-частотных кепстральных коэффициентов и применение метода главных компонент. Нейроэволюционный метод обучения ИНС является опциональным этапом алгоритма.
В результате тестирования алгоритма были найдены его оптимальные параметры. Это количество MFCC – 14 и количество главных компонент – 7. Эти параметры обеспечивают высокую точность (более 90 %) при минимизации числа используемых признаков.
Метод главных компонент позволил нам сделать входные данные более компактными, уменьшить пространство признаков (с 14 до 7) и соответственно найти наиболее оптимальную поверхность решения. На рис. 3 показаны пространства признаков MFCC (а) и PCA (б) (три первых составляющих, 3D-вид). Можно заметить, что данные располагаются более компактно и через них можно построить более простую разделяющую поверхность.


Рис. 3. Проекция данных: a – MFCC, б – PCA
Использование нейроэволюционного алгоритма Enforced Subpopulation не смогло дать более высокую точность в сравнении с методом обратного распространения ошибки. Результаты сравнения отражены в табл. 1.
Сравнение ESP и метода обратного распространения ошибки
Машинный слух. Как работает идентификация человека по его голосу
Содержание статьи
- Характеристики голоса
- Предобработка звука
- Идентификация с использованием MFCC
- Тестирование метода
- Идентификация голоса с помощью нейронных сетей
- Тестирование метода
- Выводы
Характеристики голоса
В первую очередь голос определяется его высотой. Высота — это основная частота звука, вокруг которой строятся все движения голосовых связок. Эту частоту легко почувствовать на слух: у кого-то голос выше, звонче, а у кого-то ниже, басовитее.
Другой важный параметр голоса — это его сила, количество энергии, которую человек вкладывает в произношение. От силы голоса зависит его громкость, насыщенность.
Еще одна характеристика — то, как голос переходит от одного звука к другому. Этот параметр наиболее сложный для понимания и для восприятия на слух, хотя и самый точный — как и отпечаток пальца.
Предобработка звука
Человеческий голос — это не одинокая волна, это сумма множества отдельных частот, создаваемых голосовыми связками, а также их гармоники. Из-за этого в обработке сырых данных волны тяжело найти закономерности голоса.
Нам на помощь придет преобразование Фурье — математический способ описать одну сложную звуковую волну спектрограммой, то есть набором множества частот и амплитуд. Эта спектрограмма содержит всю ключевую информацию о звуке: так мы узнаем, какие в исходном голосе содержатся частоты.
Но преобразование Фурье — математическая функция, которая нацелена на идеальный, неменяющийся звуковой сигнал, поэтому она требует практической адаптации. Так что, вместо того чтобы выделять частоты из всей записи сразу, эту запись мы поделим на небольшие отрезки, в течение которых звук не будет меняться. И применим преобразование к каждому из кусочков.
 Спектрограмма пения птицы
Спектрограмма пения птицы
Выбрать длительность блока несложно: в среднем один слог человек произносит за 70–80 мс, а интонационно выделенный вдвое дольше — 100–150 мс. Подробнее об этом можно почитать в исследовании.
Следующий шаг — посчитать спектрограмму второго порядка, то есть спектрограмму от спектрограммы. Это нужно сделать, поскольку спектрограмма, помимо основных частот, также содержит гармоники, которые не очень удобны для анализа: они дублируют информацию. Расположены эти гармоники на равном друг от друга расстоянии, единственное их различие — уменьшение амплитуды.
Давай посмотрим, как выглядит спектр монотонного звука. Начнем с волны — синусоиды, которую издает, например, проводной телефон при наборе номера.
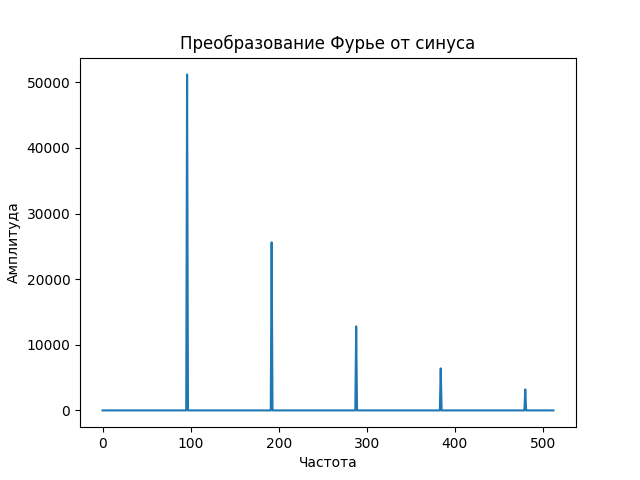
Видно, что, кроме основного пика, на самом деле представляющего сигнал, есть меньшие пики, гармоники, которые полезной информации не несут. Именно поэтому, прежде чем получать спектрограмму второго порядка, первую спектрограмму логарифмируют, чем получают пики схожего размера.
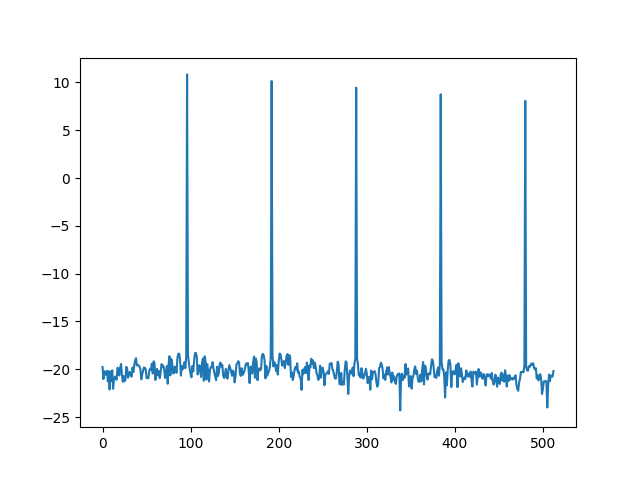 Логарифм спектрограммы синуса
Логарифм спектрограммы синуса
Теперь, если мы будем искать спектрограмму второго порядка, или, как она была названа, «кепстр» (анаграмма слова «спектр»), мы получим во много раз более приличную картинку, которая полностью, одним пиком, отображает нашу изначальную монотонную волну.
Кепстр
Одна из самых полезных особенностей нашего слуха — его нелинейная природа по отношению к восприятию частот. Путем долгих экспериментов ученые выяснили, что эту закономерность можно не только легко вывести, но и легко использовать.
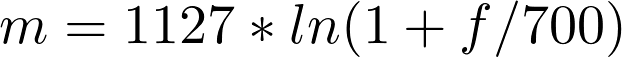 Зависимость мела от герца
Зависимость мела от герца
Эту новую величину назвали мел, и она отлично отражает способность человека распознавать разные частоты — чем выше частота звука, тем сложнее ее различить.
 График перевода герца в мелы
График перевода герца в мелы
Теперь попробуем применить все это на практике.
Идентификация с использованием MFCC
Мы можем взять длительную запись голоса человека, посчитать кепстр для каждого маленького участка и получить уникальный отпечаток голоса в каждый момент времени. Но этот отпечаток слишком большой для хранения и анализа — он зависит от выбранной длины блока и может доходить до двух тысяч чисел на каждые 100 мс. Поэтому из такого многообразия необходимо извлечь определенное количество признаков. С этим нам поможет мел-шкала.
Мы можем выбрать определенные «участки слышимости», на которых просуммируем все сигналы, причем количество этих участков равно количеству необходимых признаков, а длины и границы участков зависят от мел-шкалы.
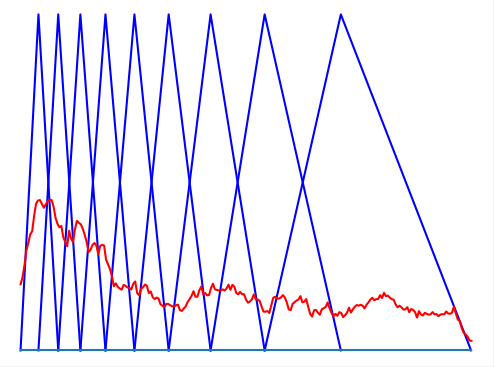 Вычисление мел-частотных кепстральных коэффициентов
Вычисление мел-частотных кепстральных коэффициентов
Вот мы и познакомились с мел-частотными кепстральными коэффициентами (MFCC). Количество признаков может быть произвольным, но чаще всего варьируется от 20 до 40.
Эти коэффициенты отлично отражают каждый «частотный блок» голоса в каждый момент времени, а значит, если обобщить время, просуммировав коэффициенты всех блоков, мы сможем получить голосовой отпечаток человека.
Тестирование метода
Давай скачаем несколько записей видео с YouTube, из которых извлечем голос для наших экспериментов. Нам нужен чистый звук без шумов. Я выбрал канал TED Talks.
Скачаем несколько видеозаписей любым удобным способом, например с помощью утилиты youtube-dl. Она доступна через pip или через официальный репозиторий Ubuntu или Debian. Я скачал три видеозаписи выступлений: двух женщин и одного мужчины.
Затем преобразуем видео в аудио, создаем несколько кусков разной длины без музыки или аплодисментов.
Теперь разберемся с программой на Python 3. Нам понадобятся библиотеки numpy для вычислений и librosa для обработки звука, которые можно установить с помощью pip . Для твоего удобства все сложные вычисления коэффициентов упаковали в одну функцию librosa.feature.mfcc . Загрузим звуковую дорожку и извлечем характеристики голоса.
Продолжение доступно только участникам
Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте
Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», увеличит личную накопительную скидку и позволит накапливать профессиональный рейтинг Xakep Score! Подробнее












