Каким кодом представлена информация в памяти компьютера

§ 6. Представление текста, изображения и звука в компьютере

В этом параграфе обсудим способы компьютерного кодирования текстовой, графической и звуковой информации. С текстовой и графической информацией конструкторы «научили» работать ЭВМ, начиная с третьего поколения (1970-е годы). А работу со звуком «освоили» лишь машины четвертого поколения, современные персональные компьютеры. С этого момента началось распространение технологии мультимедиа.

Что принципиально нового появлялось в устройстве компьютеров с освоением ими новых видов информации? Главным образом, это периферийные устройства для ввода и вывода текстов, графики, видео, звука. Процессор же и оперативная память по своим функциям изменились мало. Существенно возросло их быстродействие, объем памяти. Но как это было на первых поколениях ЭВМ, так и осталось на современных ПК — основным навыком процессора в обработке данных является умение выполнять вычисления с двоичными числами. Обработка текста, графики и звука представляет собой тоже обработку числовых данных. Если сказать еще точнее, то это обработка целых чисел. По этой причине компьютерные технологии называют цифровыми технологиями.

О том, как текст, графика и звук сводятся к целым числам, будет рассказано дальше. Предварительно отметим, что здесь мы снова встретимся с главной формулой информатики:

Смысл входящих в нее величин здесь следующий: i — разрядность ячейки памяти (в битах), N — количество различных целых положительных чисел, которые можно записать в эту ячейку.

Способы кодировки

Проанализируем разнообразные виды информации и особенности ее кодирования.

По принципу представления все информационные сведения можно классифицировать на следующие группы:

• графическая;
• аудиоинформация (звуковая);
• символьная (текстовая);
• числовая;
• видеоинформация.

Способы кодирования информации обусловлены поставленными целями, а также имеющимися возможностями,методами ее дальнейшей обработки и сохранения. Одинаковые сообщения могут отображаться в виде картинок и условных знаков (графический способ), чисел (числовой способ) или символов (символьный способ).

Соответственно происходит и классификация информации по способу кодирования:

• символьные сообщения включают знаки дорожного движения, сигналы светофора и т.д.;
• текстовые данные – это книги, нотные записи, различные документы;
• всевозможные изображения (фотографии, схемы, рисунки) представляют все многообразие графической информации.

Чтобы расшифровать сообщение, отображаемое в выбранной системе кодирования информации, необходимо осуществить декодирование – процесс восстановления до исходного материала. Для успешного осуществления расшифровки необходимо знать вид кода и методы шифрования.

Самыми распространенными видами кодировок информации являются следующие:

• преобразование текста;
• графическая кодировка;
• кодирование числовых данных;
• перевод звука в бинарную последовательность чисел;
• видеокодирование.

Различают такие методы кодирования информации как:

• метод замены (подстановки) – знаки первоначального сообщения заменяются на соответствующие символы выбранного кодового алгоритма;
• метод перестановки – символы оригинального текста меняются местами по определенной схеме;
• метод гаммирования – к исходным обозначениям добавляется случайная последовательность других знаков.

Методы измерения количества информации: вероятностный и алфавитный

Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.

Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:

Например, пусть шарик находится в одной из четырех коробок. Таким образом, имеется четыре равновероятных события (N = 4). Тогда по формуле Хартли 4 = 2 I . Отсюда I = 2. То есть сообщение о том, в какой именно коробке находится шарик, содержит 2 бита информации.

Алфавитный подход

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:

Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:

I = log₂ 32 = 5 битов.

Если N не является целой степенью 2, то число log₂N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log₂N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.

Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:

N = 26; N’ = 32; I = log₂N’ = log₂(2 5 ) = 5 битов.

Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:

Примеры решения задач

Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение. С помощью n лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 n сигналов. 2 5 < 50 < 2 6 , поэтому пяти лампочек недостаточно, а шести хватит.

Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log₂101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log₂128 = 7 битов. Для 80 измерений общий информационный объем равен:

80 · 7 = 560 битов = 70 байтов.

Ответ: 70 байтов.

Вероятностный подход

Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

где $I$ — количество информации;

$N$ — количество возможных событий;

$p_i$ — вероятность $i$-го события.

Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

Кодирование текстовой информации и компьютеры

Если смотреть на текст глазами компьютера, то в тексте нет предложений, абзацев, заголовков и т. д., потому что весь текст просто состоит из отдельных символов. Причем символами будут являться не только буквы, но и цифры, и любые другие специальные знаки (+, -,*,= и т. д.). Что самое интересное, даже пробелы, перенос строки и табуляция — для компьютера это тоже отдельные символы.

Для справки. Есть уникальный язык программирования, который в качестве своих операторов использует только пробелы, табуляции и переносы строки. Практического применения этот язык не имеет, но он есть.

Мы вводим текст в компьютер при помощи клавиатуры, символы которой мы прекрасно понимаем. Нажимая на какую-то букву, мы отправляем в оперативную память компьютера двоичное представление нажатых клавиш. Каждый отдельный символ будет представлен 8-битной кодировкой. Например буква «А» — это «11000000». Получается, что один символ — это 1 байт или 8 бит. При такой кодировке, путем нехитрых подсчетов можно посчитать, что мы можем зашифровать 256 символов. Для кодирования текстовой информации данного количества символов более чем предостаточно.

Кодирование текстовой информации в компьютерных устройствах сводится к тому, что каждому отдельному символу присваивается уникальное десятичное значение от 0 и до 255 или его эквивалент в двоичной форме от 00000000 и до 11111111. Люди могут различать символы по их внешнему виду, а компьютерное устройство только по их уникальному коду.

Рассмотрите, как происходит процесс. Мы нажимаем нужный нам символ на клавиатуре, ориентируясь на их внешний вид. В оперативную память компьютера он попадает в двоичном представлении, а когда компьютер его выводит нам на экран, то происходит процесс декодирования, чтобы мы увидели знакомый нам символ.

Метод координат

Любые данные можно передать с помощью двоичных чисел, в том числе и графические изображение, представляющие собой совокупность точек. Чтобы установить соответствие чисел и точек в бинарном коде, используют метод координат.

Метод координат на плоскости основан на изучении свойств точки в системе координат с горизонтальной осью Ox и вертикальной осью Oy. Точка будет иметь 2 координаты.

Если через начало координат проходит 3 взаимно перпендикулярные оси X, Y и Z, то используется метод координат в пространстве. Положение точки в таком случае определяется тремя координатами.

Система координат в пространстве

Алгоритм представления в компьютере беззнаковых целых чисел

Беззнаковое целое положительное число перевести в двоичную систему счисления.

Записать число в $8$ разрядах так, чтобы младший разряд числа соответствовал младшему разряду ячейки.

Дополнить число, если необходимо, слева нулями до нужного числа разрядов ($8$-ми, $16$-ти, $32$-х).

Получить 8-разрядное представление числа $30$.

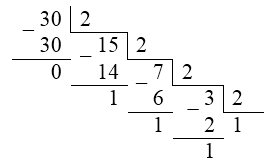
Дополним до $8$-ми разрядов:

Представление вещественных чисел

Любое вещественное число А может быть записано в экспоненциальной форме:

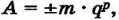
где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Например, число 472 ООО ООО может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.

Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».

Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 10 9 .

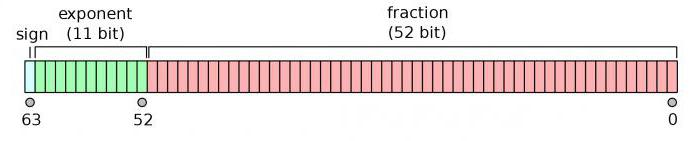
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа:

0,11111111111111111111111 • 10 1111111

Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

Плавающая запятая

Это последнее, что вам необходимо знать про представление чисел в компьютере. Поскольку при записи дробей возникает проблема определения положения запятой в них, для размещения подобных цифр в компьютере используется экспоненциальная форма.

Любое число может быть представлено в следующей форме Х = m * р п . Где m – это мантисса числа, р – основание системы счисления и п – порядок числа.

Для стандартизации записи чисел с плавающей запятой используется следующее условие, согласно которому модуль мантиссы должен быть больше или равен 1/п и меньше 1.

Пусть нам дано число 666,66. Приведём его к экспоненциальной форме. Получится Х = 0,66666 * 10 3 . Р = 10 и п = 3.

На хранение значений с плавающей запятой обычно выделяется 4 или 8 байт (32 или 64 бита). В первом случае это называется числом обычной точности, а во втором – двойной точности.

Из 4 байт, выделенных под хранение цифр, 1 (8 разрядов) отдается под данные о порядке и его знаке, а 3 байта (24 разряда) уходят на хранение мантиссы и её знака по тем же принципам, что и для целочисленных значений. Зная это, мы можем провести нехитрые расчеты.

Максимальное значение п = 1111111 2 = 127 10 . Исходя из него, мы можем получить максимальный размер числа, которое может храниться в памяти компьютера. Х=2 127 . Теперь мы можем вычислить максимально возможную мантиссу. Она будет равна 2 23 – 1 ≥ 2 23 = 2 (10 × 2,3) ≥ 1000 2,3 = 10 (3 × 2,3) ≥ 10 7 . В итоге, мы получили приближенное значение.

Если теперь мы объединим оба расчета, то получим значение, которое может быть записано без потерь в 4 байта памяти. Оно будет равно Х = 1,701411 * 10 38 . Остальные цифры были отброшены, поскольку именно такую точность позволяет иметь данный способ записи.

Час правового общения «Правовой всеобуч» с адвокатом Витебской областной коллегии адвокатов

19 и 21 апреля 2022 года в колледже состоялась встреча обучающихся группы ПЗ-58 с адвокатом Витебской областной коллегии адвокатов № 1 г.Витебска Наумик А.М. В рамках мероприятия были освещены вопросы привлечения к административной и уголовной ответственности несовершеннолетних согласно КоАП и УК Республики Беларусь. Обучающиеся смогли получить юридическую консультацию по защите своих прав и интересов.