Как решить систему уравнений в excel

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Как решить систему уравнений в Excel

Поиск корней системы уравнений иногда может вызывать особенные сложности, особенно, когда эти уравнения имеют огромные размеры и степени возведения. Эксель может легко справиться с поставленной задачей различными способами.

Для того чтобы решить любую систему уравнений необходимо найти все ее корни. Сделать можно следующими способами:

1. Матричный метод.

Этот метод является самым популярным способ поиска корней системы. Для этого достаточно построить прямую и обратную матрицу с коэффициентами и решить ее.

Допустим, у нас есть система уравнений, к примеру:

14×1+2×2+8×4=218
7×1-3×2+5×3+12×4=213
5×1+x2-2×3+4×4=83
6×1+2×2+x3-3×4=21

Построим матрицу коэффициентов с учетом некоторых особенностей:

• Обязательно следовать порядку нахождения чисел.
• Отсутствие корней принято считать за равным «0».
• Если нет коэффициента при существующем корне, коэффициент принято считать равным «1».

Заполняем матрицу А значениями.

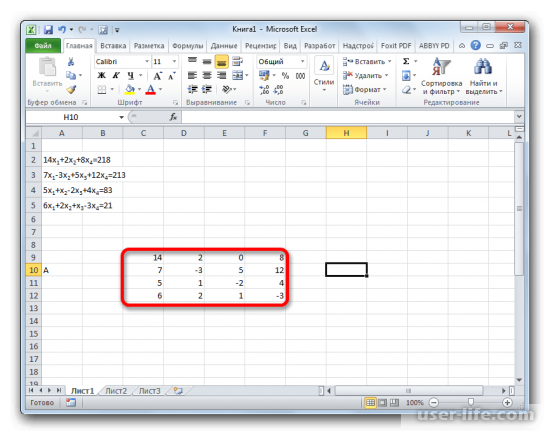
Заполняем матрицу B значениями, которые следуют после знака «=».

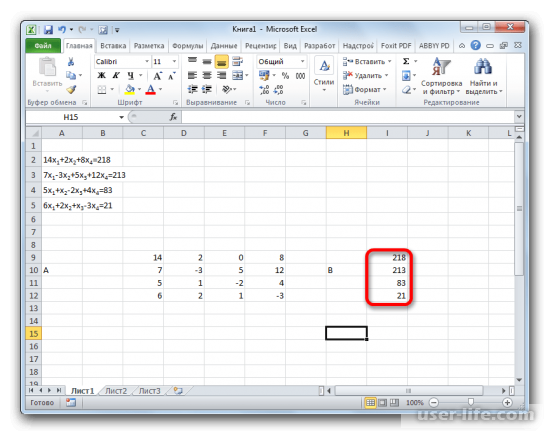
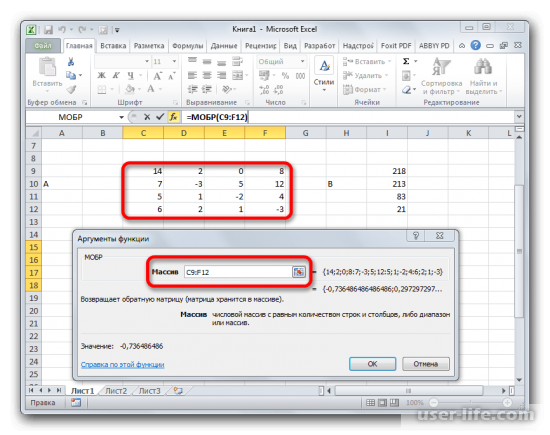
Поиск корней системы уравнения прежде всего начинается с поиска обратной матрицы. За это отвечает оператор «МОБР» и выглядит он так: «=МОБР(массив)».

Определяем позицию для будущей матрицы, учитывая, что, размер обратной матрицы должен равняться размеру первичной матрицы. Открываем «Мастер функций».

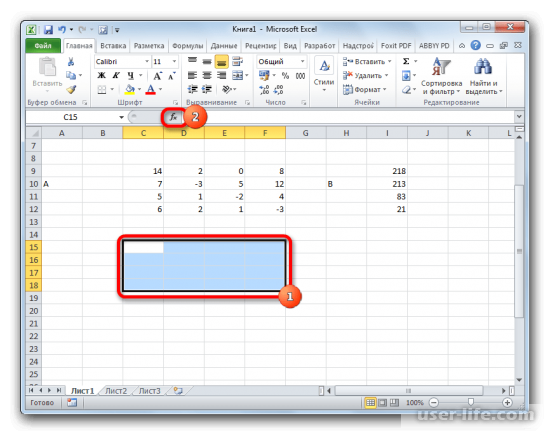
В диалоговом коне находим функцию «МОБР» и применяем операцию.

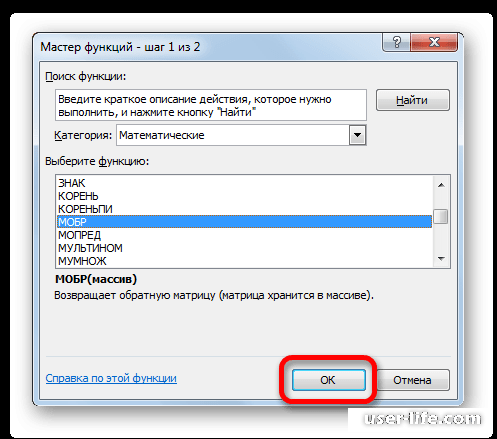
Диапазон нашего массива А занесем в поле «Массив» и нажимаем кнопки «Ctrl+Shift+Enter». Зачем? При проведении операций с массивами данных кнопка «Enter» означает лишь ввод.

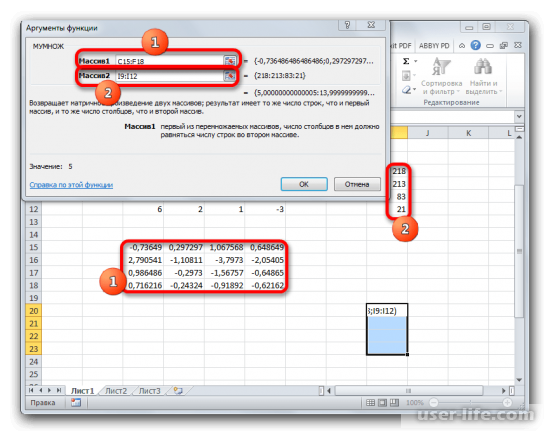
Получив обратную матрицу необходимо произвести умножение на матрицу В. За умножение матриц отвечает функция «МУМНОЖ», которая выглядит следующим образом: =МУМНОЖ(Массив1;Массив2).

Определяем область для будущих значений и вставляем оператор, после чего укажем оба массива и нажимаем кнопки «Ctrl+Shift+Enter».

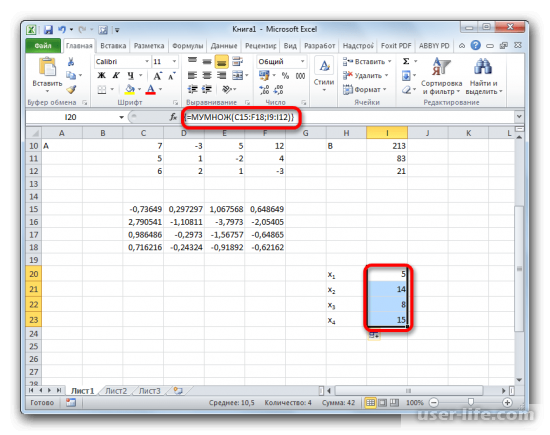
Найдены четыре корня уравнений матричным способом. Для проверки результатов нужно подставить корни в систему, и в случае совпадения равенства, можно считать достоверность решения.

2. Поиск корней системы уравнений на основе подбора параметров.

Этот метод для поиска корней заключается в том, что, имея уже готовый результат необходимо выполнить поиск всех неизвестных значений.

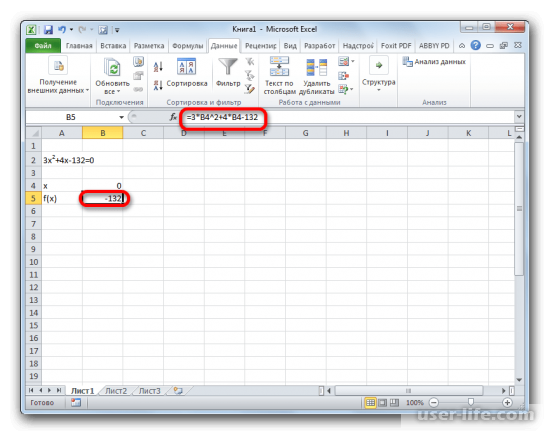
К примеру, есть уравнение, которое имеет следующий вид: 3x 2+4x-132=0. Допустим, что «х» = «0». Найдем f(x), используя занеся исходные значения в ячейку «=3*x 2+4*x-132», где в поле «х» укажем значение ячейки.

Для вызова оператора «Подбора параметра» необходимо перейти во вкладку «Данные» — «Анализ».

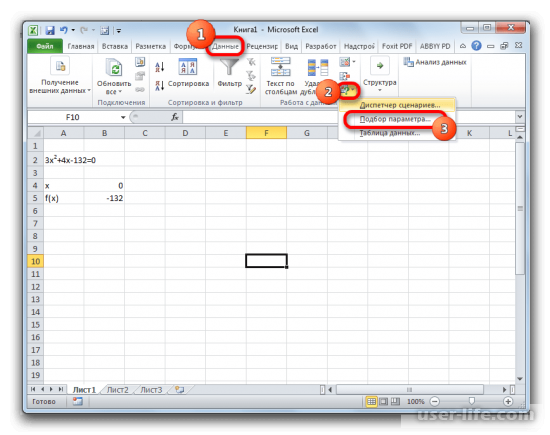
В диалоговом окне укажем следующие значения:

• «Установить в ячейке»: укажем ячейку с формулой;
• «Значение»: — «0»;
• «Изменяя значения: укажем ячейку со значением «х».

После чего можно применить оператор.

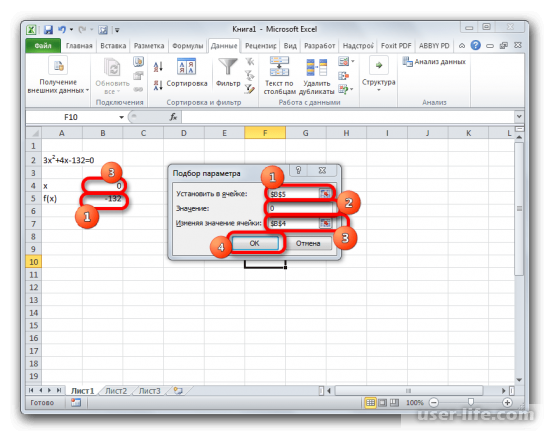
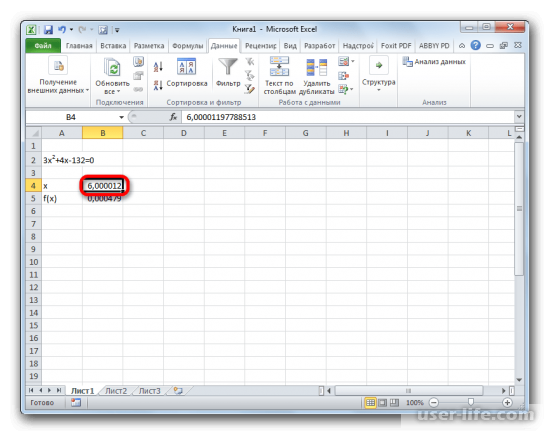
Достоверность полученных корней можно проверить путем ввода значения в уравнение.

3. Метод Крамера

Найти корни также можно с помощью метода Крамера, который основывается на поиске определителей.
Допустим, наша система выглядит следующим образом:

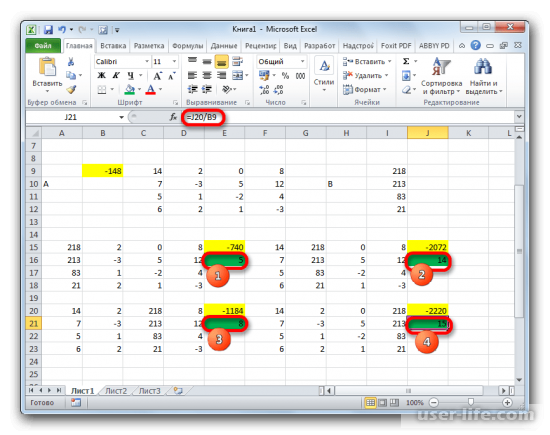
14×1+2×2+8×4=218
7×1-3×2+5×3+12×4=213
5×1+x2-2×3+4×4=83
6×1+2×2+x3-3×4=21

Создаем массивы значений, опираясь то, как это было сделано ранее, занося коэффициенты уравнений, учитывая несколько правил.

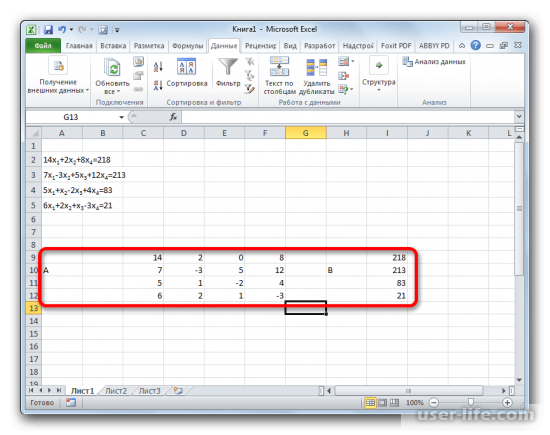
Теперь нужно создать еще четыре сводных матрицы, взяв за основу матрицу А с заменой каждого столбца на матрицу В. То есть, первая матрица будет копией матрицы А, за исключением того, что ее первый столбец будет матрицей В, и так далее.

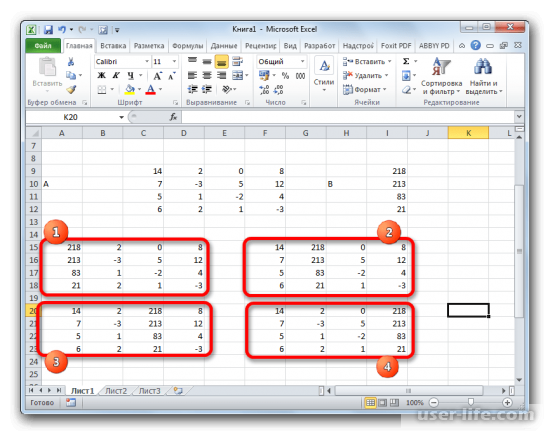
Следующим шагом будет поиск определителя для каждой из матриц. Стоит учесть, решение можно будет найти лишь в том случае, если каждый из определителей будет отличным от «0».
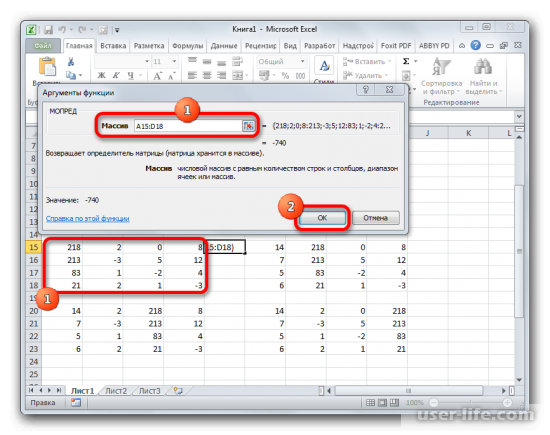
Используя оператор «МОПРЕД» находим определители, указывая вместо аргумента «массив» каждую из матриц.

Подобным способом необходимо найти определители для всех указанных матриц.

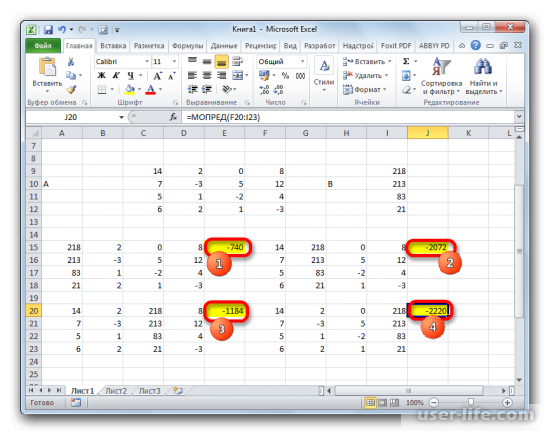
Нахождение решение уравнения методом Крамера заключается в том, что найденные определители матриц необходимо разделить на тот же определитель, но первичной матрицы.

Нам осталось найти этот определитель, после чего можно приступить к поиску непосредственно самих корней системы. Используя ту же функцию «МОПРЕД» находим определитель первичной матрицы.

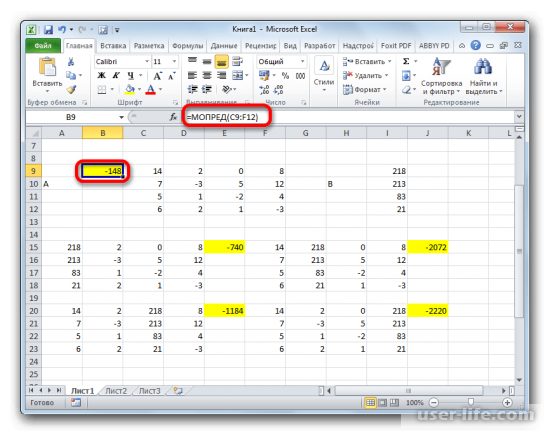
Последним шагом станет поиск самих корней. Делим полученные определители матриц на определитель первичной матрицы и получаем решение системы уравнений.

Как видим, поиск корней системы уравнений может не составлять особого труда – функционал программы может справиться с любой поставленной задачей, достаточно лишь понимать, как работают операторы и знать простые правила математических операций.

Решение системы уравнений графическим методом средствами MS Excel

Цели и задачи.

1. Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
2. Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
3. Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
4. Закрепить навыки создания таблиц и диаграмм.
5. Научить решать систему уравнений графическим методом, исследовать график функции.

Оборудование урока: компьютеры, мультимедиа проектор.

Программное обеспечение: Windows XP, пакет программ MS Office 2003.

Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.

Запишите в тетради тему урока и укажите дату.

Назовите мне кого из класса сегодня нет.

Давайте вспомним, что такое уравнение, и как его можно решить графически.

Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.

(Учащиеся приводят определения)

Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.

Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).

Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.

Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.

Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.

Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.

Но эту задачу может взять на себя ЭВМ.

Мы воспользуемся возможностями программы MS Excel.

Основная часть

Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.

Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.

С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.

И так. Мы запустили программу MS Excel.

Мы хотим разработать таблицу для решения системы уравнений:

Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.

Сформируем начальные данные.

В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.

В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.

Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.

Формулы, которые нам нужно ввести приведены на рисунке.

Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.

Заполните, пожалуйста, в каждой таблице 20-25 строчек.

Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.

Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.

Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.

Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.

Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.

Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.

У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.

Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.

Мы видим, что одно из решений нашей системы уравнений равно -1,5.

Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.

Сколько у вас получилось?

Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.

Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.

Для этого нужно внести изменения в таблицу и расчётные формулы.

Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.

Самостоятельно внесите все необходимые изменения.

Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.

Заключительный этап урока

Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?

А что легче для вас?

Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.

Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.

Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Как я могу решить систему линейных уравнений в Excel?

У меня есть система из 22 линейных уравнений (ровно 22 уравнения и 22 неизвестных), которые динамически генерируются в электронной таблице Excel. Есть ли способ, чтобы Excel решал систему и производил значение для каждой из неизвестных переменных?

В другом вопросе SO есть много хорошей информации об алгоритмах, используемых для решения таких уравнений. Правило Крамера, в частности, выглядит многообещающим, но я не уверен, как его реализовать в Excel.

Любая помощь приветствуется!

• Сохранение структуры моей матрицы при записи для использования в excel (заголовки столбцов)
• Возврат соответствующей даты максимального значения
• Матричные функции для вычисления корреляционной матрицы в сочетании с оператором IF
• Как использовать вложенный цикл для ячейки Matrix в excel vba
• VBA Сумма двух 2D-массивов на разных листах
• Вычислить матрицу в excel, содержащую 0 значений на основе итогов столбцов и строк
• Массив матрицы Excel с использованием выпадающих списков
• Microsoft Excel — как преобразовать вертикальный список с удвоенным идентификатором в горизонтальный без дублирования

На этой странице представлен следующий простой способ:

1. Введите матрицу коэффициентов в диапазоне nxn.

2. Введите вектор констант в столбце n-tall. Выберите пустой столбец n-tall. Важно, чтобы вы не выбрали только одну ячейку.

3. Тип, = MMULT (MINVERSE (rates_matrix_range), constants_vector_range) в текстовом поле формулы и нажмите [CTRL] [SHIFT] [ENTER]. Важно, чтобы вы просто не нажимали [ENTER].

Это должно работать адекватно, поскольку у вас есть только небольшая система (22×22). Хотя, в идеале, вы не должны инвертировать матрицу напрямую, в этом случае это не имеет значения.

Вы определенно не хотите правила Крамера. Из-за его довольно плохих численных свойств это скорее теоретический, чем практический интерес.

Что относительно Microsoft Solver Foundation ? Кажется, я помню, что есть пример небольшого набора одновременных уравнений в документации, которая поставляется с экспресс-версией.

Вы никогда не должны рассматривать правило Крамера для решения линейной системы! Это настолько неэффективно, что невозможно выполнить даже для небольших систем.

Excel не является правильным инструментом для решения линейной системы. Если бы я был вами, я бы написал простой скрипт python, который читает файл excel, решает уравнение (с numpy) и сохраняет результат в файле, который Excel может читать. (даже лучше, избегайте Excel вообще, если можете).

Функция Excel LINEST должна сделать это – и в большинстве случаев вернет лучшие результаты, чем MMULT (MINVERSE (…) …).

Вы также можете найти полезные функции LOGEST, GROWTH и TREND.

Если у вас есть проблемы с обратным матричным вычислением, например, над / под потоком / усечением и т. Д., Вы всегда можете использовать Solver – иначе получите копию числовых рецептов на C и переведите в VBA.

который может быть решателем линейных уравнений, мы можем сделать с математическим решателем, используя математическое уравнение корня, лежит между еще двумя числами экспоненциальной части решателя, но найти лучший способ решения линейного уравнения.