Как изменяется емкость конденсатора при наличии диэлектрика

Электроёмкость плоского конденсатора. Геометрические характеристики плоского конденсатора полностью определяются площадью S его пластин и расстоянием d между ними. От этих величин и должна зависеть ёмкость плоского конденсатора.

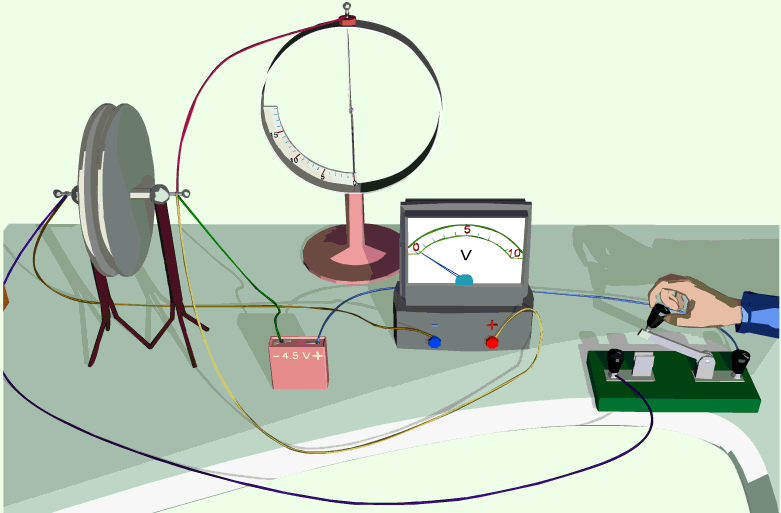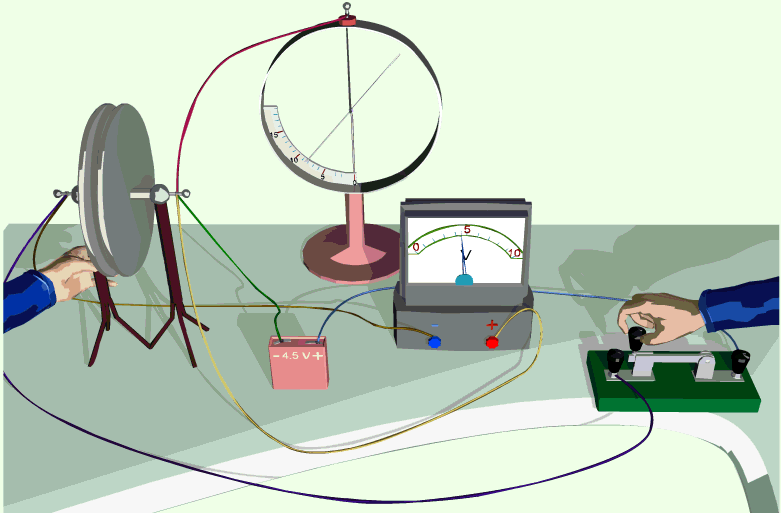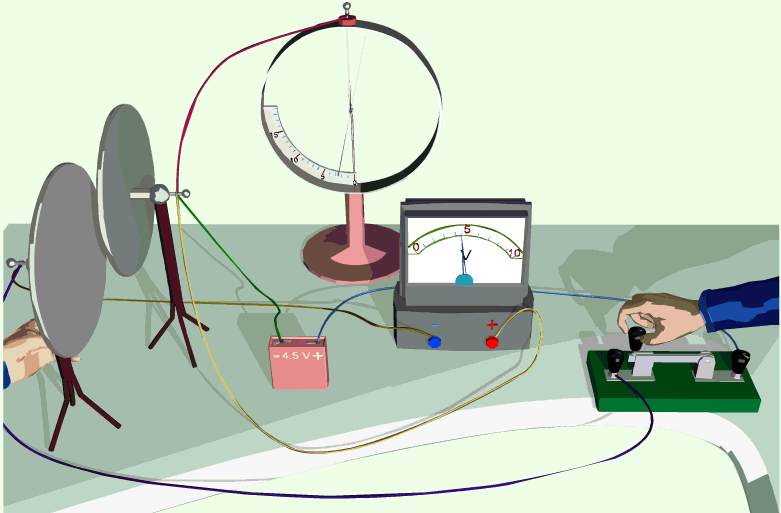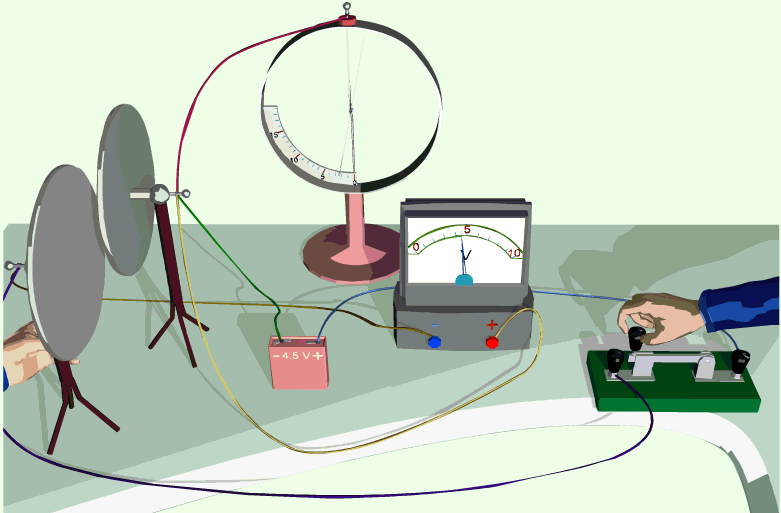
Проверьте на опыте зависимость электроёмкости конденсатора от его геометрических характеристик. Для этого возьмите две металлические плоские пластины и зарядите одну из них (например, потрите о шёлк стеклянную палочку), приблизьте другую пластину к ней и затем заземлите её. Соедините пластины с вольтметром. Уменьшайте расстояние между пластинами и следите за изменением показаний вольтметра. Сдвигайте пластины друг относительно друга и также следите за изменением показаний вольтметра. Сделайте выводы.

Чем больше площадь пластин, тем больший заряд можно на них накопить: q

S. Напряжение же между пластинами согласно формуле (14.21, с. 314) пропорционально расстоянию между ними. Поэтому ёмкость

Кроме того, ёмкость конденсатора зависит от свойств диэлектрика между пластинами. Так как диэлектрик ослабляет поле, то электроёмкость при наличии диэлектрика увеличивается: 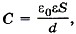где ε — диэлектрическая проницаемость диэлектрика.

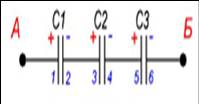
Последовательное и параллельное соединения конденсаторов. На практике конденсаторы часто соединяют различными способами. На рисунке 14.40 представлено последовательное соединение трёх конденсаторов. Если точки 1 и 2 подключить к источнику напряжения, то на левую пластину конденсатора С1 перейдёт заряд +qy на правую пластину конденсатора СЗ — заряд -q. Вследствие электростатической индукции правая пластина конденсатора С1 будет иметь заряд -q, а так как пластины конденсаторов С1 и С2 соединены и до подключения напряжения были электро нейтральны, то по закону сохранения заряда на левой пластине конденсатора С2 появится заряд +q и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по модулю заряд:

Важно
Определить эквивалентную электроёмкость — это значит определить электроёмкость такого конденсатора, который при той же разности потенциалов будет накапливать тот же заряд q, что и система конденсаторов.

Разность потенциалов φ1 — φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов:

Воспользовавшись формулой (14.23), запишем:

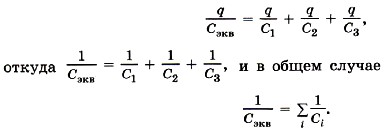
На рисунке 14.41 представлена схема параллельно соединённых конденсаторов. Разность потенциалов между пластинами всех конденсаторов одинакова и равна:

Заряды на пластинах конденсаторов

На эквивалентном конденсаторе ёмкостью С_экв заряд на пластинах при той же разности потенциалов

Для электроёмкости, согласно формуле (14.23) запишем: C_эквU = C₁U + C₂U + C₃U, следовательно, С_экв = C₁+ С₂ + С₃, и в общем случае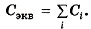

Различные типы конденсаторов. В зависимости от назначения конденсаторы имеют различное устройство. Обычный технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свёрнуты в пакет небольшого размера.

В радиотехнике широко применяют конденсаторы переменной электроёмкости (рис. 14.42). Такой конденсатор состоит из двух систем металлических пластин, которые при вращении рукоятки могут входить одна в другую. При этом меняются площади перекрывающихся частей пластин и, следовательно, их электроёмкость. Диэлектриком в таких конденсаторах служит воздух. Сейчас во многих устройствах электроёмкость конденсаторов регулируется электронными устройствами.

Значительного увеличения электроёмкости за счёт уменьшения расстояния между обкладками достигают в так называемых электролитических конденсаторах (рис. 14.43). Диэлектриком в них служит очень тонкая плёнка оксидов, покрывающих одну из обкладок (полосу фольги). Другой обкладкой служит бумага, пропитанная раствором специального вещества (электролита).

Ключевые слова для поиска информации по теме параграфа.
Электроёмкость. Конденсатор. Виды конденсаторов

Вопросы к параграфу

1. Что называют электроёмкостью двух проводников?

2. Почему понятие электроёмкости неприменимо к диэлектрикам?

3. От чего зависит электроёмкость?

4. Как изменяется ёмкость конденсатора при наличии диэлектрика между его обкладками?

5. Какие существуют типы конденсаторов?

6. Какую роль выполняют конденсаторы в технике?

Как изменяется емкость конденсатора при наличии диэлектрика

100.2. Как изменяется емкость конденсатора при наличии диэлектрика между его обкладками

Задача из пособия: Мякишев, Буховцев, Сотский, 10 класс
Глава 14. Электростатика

Решение

В большинстве конденсаторов между пластинами проложен изолирующий материал (диэлектрик), например, бумага или пластмассовая пленка. Этим достигается сразу несколько целей. Во-первых, диэлектрики лучше противостоят электрическому пробою, чем воздух, и к конденсатору можно приложить более высокое напряжение без утечки заряда через зазор между обкладками. Во-вторых, при наличии прокладки из диэлектрика пластины можно расположить ближе друг к другу без опасения, что они могут соприкасаться. Наконец, экспериментально обнаружено, что при заполнении пространства между пластинами диэлектриком его емкость увеличивается в К раз, т.е.

где С — емкость, отвечающая вакууму между обкладками, а С — емкость в случае, когда пространство между пластинами заполнено диэлектриком. Множитель К называют относительной диэлектрической проницаемостью; значения К для ряда диэлектриков приведены в табл. 25.1.
Обратите внимание на то, что для воздуха при давлении 1 атм К = 1,0006, и поэтому емкость конденсатора с воздушным зазором очень мало отличается от емкости этого конденсатора в вакууме.

Для плоского конденсатора:

С = Кε A/d — [плоский конденсатор] (25.8),

когда пространство между пластинами целиком заполнено диэлектриком с диэлектрической проницаемостью К. Величина Кε так часто встречается в формулах, что нередко вводят величину

которую называют абсолютной диэлектрической проницаемостью. Тогда емкость плоского конденсатора принимает вид

Напомним, что ε — это электрическая постоянная. Плотность энергии, запасенной электрическим полем Е

Влияние диэлектрика на емкость впервые всесторонне исследовал Фарадей. Он обнаружил, что, когда пространство между пластинами конденсатора заполнено диэлектриком, на пластинах при том же напряжении накапливается несколько больший заряд, нежели когда между пластинами воздух. Иначе говоря, если заряд на каждой пластине конденсатора с воздушным промежутком равен Q , то после введения диэлектрика и подключения конденсатора к батарее с прежним напряжением V заряд каждой из пластин увеличится до

Q = KQ [при постоянном напряжении] .

Это соответствует формуле (25.7), поскольку после введения диэлектрика емкость равна

где С = Q /V — емкость в отсутствие диэлектрика.

Рассмотрим теперь несколько иной случай (выше мы, вводя диэлектрик, поддерживали напряжение постоянным). Пусть пластины конденсатора, подключенного к батарее с напряжением V , приобретают заряд

Прежде чем ввести диэлектрик, отключим конденсатор от батареи. После введения диэлектрика (который заполняет все пространство между пластинами) заряд Q на каждой из пластин не изменится. В этом случае мы обнаружим, что разность потенциалов между пластинами уменьшится в К раз:

Емкость же вновь будет равна

Оба этих результата согласуются с выражением (25.7).

Электрическое поле внутри диэлектрика также изменяется. При отсутствии диэлектрика между пластинами напряженность электрического поля между обкладками плоского конденсатора определяется формулой (24.3):

где V — разность потенциалов между пластинами, a d — расстояние между ними.
Если конденсатор изолирован, так что заряд на пластинах после введения диэлектрика не изменяется, то разность потенциалов упадет до значения V = V /K. Напряженность электрического поля в диэлектрике теперь будет равна

Таким образом, напряженность электрического поля внутри диэлектрика также ослабляется в К раз. Электрическое поле внутри диэлектрика (изолятора) ослабляется, но, не до нуля, как в случае проводника.

Происходящее в диэлектрике можно объяснить с молекулярной точки зрения. Рассмотрим конденсатор, обкладки которого разделены воздушным «промежутком. На одной обкладке имеется заряд +Q, на другой заряд -Q (рис. 25.7, а).

Конденсатор изолирован (не подключен к батарее). Разность потенциалов между пластинами V определяется выражением (25.1): Q = C V . (Индекс 0 соответствует воздуху между пластинами.) Введем теперь между пластинами диэлектрик (рис. 25.7, b). Молекулы диэлектрика могут быть полярными — иначе говоря, они могут обладать постоянным дипольным моментом, будучи нейтральными. В электрическом поле возникнет вращательный момент, который будет стремиться развернуть диполи параллельно полю (рис. 25.7, b); тепловое движение препятствует идеальной ориентации всех молекул, однако, чем сильнее поле, тем выше будет степень выстроенности молекул. Даже если молекулы не полярны, в электрическом поле между обкладками у них произойдет разделение заряда, и молекулы приобретут индуцированный (наведенный) дипольный момент: электроны, не отрываясь от молекулы, сместятся в сторону положительной обкладки. Поэтому картина всегда будет такой, как показано на рис. 25.7, b. В конечном итоге все выглядит так, как если бы на обращенной к положительной обкладке внешней стороне диэлектрика имелся результирующий отрицательный заряд, а на противоположной — положительный (рис. 25.7, c). Из-за появления на диэлектрике этого индуцированного заряда часть электрических силовых линий не пройдет сквозь диэлектрик, а будет заканчиваться (или начинаться) на зарядах, наведенных на его поверхности. Соответственно напряженность электрического поля внутри диэлектрика окажется меньше, чем в воздухе.

Можно представить себе эту картину и по-иному (рис. 25.7, d). Напряженность электрического поля внутри диэлектрика представляет собой векторную сумму напряженности поля Е , создаваемого «свободными» зарядами на обкладках, и напряженности поля Е_инд, создаваемого зарядами, индуцированными в диэлектрике; поскольку эти поля направлены в противоположные стороны, результирующая напряженность электрического поля внутри диэлектрика Е — Е_инд будет меньше Е . Точное соотношение дается формулой (25.10):

Из соображений симметрии ясно, что, если размеры пластин велики по сравнению с расстоянием между ними, заряд, индуцированный на поверхности диэлектрика, не зависит от того, заполняет ли диэлектрик все пространство между пластинами или нет, если только его поверхности параллельны обкладкам. Формула (25.10) справедлива и в этом случае, хотя равенство V = V /K уже не верно (почему?). Электрическое поле между двумя параллельными пластинами связано с поверхностной плотностью заряда σ выражением

Таким образом, где σ = Q/A — поверхностная плотность заряда на обкладке, а Q — полный заряд проводника, называемый часто свободным зарядом (поскольку в проводнике заряды могут свободно перемещаться). Аналогично мы определим поверхностную плотность индуцированного заряда σ_инд

где E_инд — напряженность электрического поля, создаваемого индуцированным зарядом Q_инд = σ_индA на поверхности диэлектрика (рис. 25.7, г); Q_инд называют обычно связанным зарядом (так как в диэлектрике (изоляторе) заряды не могут свободно перемещаться). Поскольку, как показано выше, Е_инд = Е (1 — 1/К), получаем

Так как К больше 1, индуцированный на диэлектрике заряд всегда меньше заряда на обкладках конденсатора.

Продолжение следует. Коротко о следующей публикации:

Плоский воздушный конденсатор с диэлектриком между пластинами подключён к аккумулятору. Не отключая конденсатор от аккумулятора, диэлектрик удаляют из конденсатора. Как изменятся при этом ёмкость конденсатора и разность потенциалов между его обкладками?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

Ёмкость конденсатора

Разность потенциалов между
обкладками конденсатора

Ёмкость плоского воздушного конденсатора рассчитывается по формуле: следовательно, при удалении диэлектрика уменьшится диэлектрическая постоянная а значит ёмкость уменьшается. Конденсатор не отключают от аккумулятора, значит, разность потенциалов между обкладками конденсатора сохраняется.

Уроки по физике и астрономии

Для увлеченных

Боковая колонка

Электроёмкость. Конденсаторы. Энергия заряженного конденсатора.

03. Электродинамика
10 класс

Единицы электроёмкости.

Предположите, при каком условии можно накопить на проводниках большой электрический заряд.

При электризации двух проводников между ними появляется электрическое поле и возникает разность потенциалов (напряжение). С увеличением заряда проводников электрическое поле между ними усиливается.

В сильном электрическом поле возможен так называемый пробой диэлектрика: между проводниками проскакивает искра, и они разряжаются. Чем меньше увеличивается напряжение и соответственно напряжённость поля между проводниками с увеличением их зарядов, тем больший заряд можно на них накопить.

Физическая величина, характеризующая способность проводников накапливать электрический заряд, называется электроёмкостью.

Напряжение U между двумя проводниками пропорционально электрическим зарядам, которые находятся на проводниках (на одном +q, а на другом -q). Действительно, если заряды удвоить, то напряжённость электрического поля станет в 2 раза больше, соответственно в 2 раза увеличится и работа, совершаемая полем при перемещении заряда из одной точки поля в другую, т. е. в 2 раза увеличится напряжение. Поэтому отношение заряда q одного из проводников к разности потенциалов между проводниками не зависит от заряда. Оно определяется геометрическими размерами проводников, их формой и взаимным расположением, а также электрическими свойствами окружающей среды.

Это позволяет ввести понятие электроёмкости двух проводников.

Электроёмкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между ними:

Электроёмкость уединённого проводника равна отношению заряда проводника к его потенциалу, если все другие проводники бесконечно удалены и потенциал бесконечно удалённой точки равен нулю.

Чем больше электроёмкость, тем больший заряд скапливается на проводниках при одном и том же напряжении. Обратим внимание, что сама электроёмкость не зависит ни от сообщённых проводникам зарядов, ни от возникающего между ними напряжения.

Единицей электроёмкости в СИ является фарад.

1 фарад — это электроёмкость двух проводников в том случае, если при сообщении им зарядов +1 Кл и -1 Кл между ними возникает разность потенциалов 1 В: 1 Ф = 1 Кл/В.

Из-за того что заряд в 1 Кл очень велик, ёмкость 1 Ф оказывается очень большой. Поэтому на практике часто используют доли этой единицы: микрофарад (мкФ) — 10 -6 Ф и пикофарад (пФ) — 10 -1 2 Ф.

Конденсатор.

Устройства для накопления электрического заряда называются конденсаторами.

Слово «конденсатор» в переводе на русский язык означает «сгуститель». В данном случае — «сгуститель электрического поля».

Конденсатор представляет собой два проводника, разделенные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники конденсатора называются обкладками.

Простейший плоский конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга.

Если заряды пластин одинаковы по модулю и противоположны по знаку, то силовые линии электрического поля начинаются на положительно заряженной обкладке конденсатора и оканчиваются на отрицательно заряженной. Поэтому почти всё электрическое поле сосредоточено внутри конденсатора и однородно.

Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника напряжения, например к полюсам батареи аккумуляторов. Можно также первую обкладку соединить с полюсом батареи, у которой другой полюс заземлён, а вторую обкладку конденсатора заземлить. Тогда на заземлённой обкладке останется заряд противоположный по знаку и равный по модулю заряду незаземлённой обкладки. Такой же по модулю заряд уйдёт в землю.

Заземление проводников — это соединение их с землёй (очень большим проводником) с помощью металлических листов в земле, водопроводных труб и т. д.

Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок.

Электроёмкость конденсатора определяется формулой (14.22).

Электрические поля окружающих тел почти не проникают внутрь конденсатора и не влияют на разность потенциалов между его обкладками. Поэтому электроёмкость конденсатора практически не зависит от наличия вблизи него каких-либо других тел.

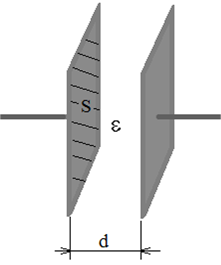
Электроёмкость плоского конденсатора. Геометрические характеристики плоского конденсатора полностью определяются площадью S его пластин и расстоянием d между ними. От этих величин и должна зависеть ёмкость плоского конденсатора.

Чем больше площадь пластин, тем больший заряд можно на них накопить: q

S. Напряжение же между пластинами согласно формуле (14.21) пропорционально расстоянию между ними. Поэтому ёмкость

где ε – диэлектрическая проницаемость диэлектрика.

Последовательное и параллельное соединения конденсаторов. На практике конденсаторы часто соединяют различными способами. На рисунке 14.40 представлено последовательное соединение трёх конденсаторов. Если точки 1 и 2 подключить к источнику напряжения, то на левую пластину конденсатора С1 перейдёт заряд +q, на правую пластину конденсатора С3 – заряд –q. Вследствие электростатической индукции правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и до подключения напряжения были электронейтральны, то по закону сохранения заряда на левой пластине конденсатора С2 появится заряд +q и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по модулю заряд:

Определить эквивалентную электроёмкость — это значит определить электроёмкость такого конденсатора, который при той же разности потенциалов будет накапливать тот же заряд q, что и система конденсаторов.

Разность потенциалов φ₁ – φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов:

Воспользовавшись формулой (14.23), запишем:

На рисунке 14.41 представлена схема параллельно соединённых конденсаторов. Разность потенциалов между пластинами всех конденсаторов одинакова и равна:

На эквивалентном конденсаторе ёмкостью С_экв заряд на пластинах при той же разности потенциалов

Для электроёмкости, согласно формуле (14.23) запишем: C_эквU = С₁U + C₂U + C₃U, следовательно, С_экв = С₁ + С₂ + С₃, и в общем случае

Энергия заряженного конденсатора.

Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта работа не пропадает, а идёт на увеличение энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, содержащую лампу накаливания, рассчитанную на напряжение в несколько вольт (рис. 14.44). При разрядке конденсатора лампа вспыхивает. Энергия конденсатора превращается в тепло и энергию излучения.

Выведем формулу для энергии плоского конденсатора.

Напряжённость поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряжённость поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределённый по поверхности другой пластины (рис. 14.45). Согласно формуле (14.14) потенциальная энергия заряда в однородном поле равна:

где q — заряд конденсатора, a d — расстояние между пластинами.

Так как Ed = U, где U — разность потенциалов между обкладками конденсатора, то его энергия равна:

Если заряд на пластинах остаётся постоянным, при сближении пластин поле совершает положительную работу:

При этом энергия электрического поля уменьшается.

Заменив в формуле (14.25) разность потенциалов или заряд с помощью выражения (14.22) для электроёмкости конденсатора, получим

Можно доказать, что эти формулы справедливы для любого конденсатора, а не только для плоского.

Энергия электрического поля. Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напряжённость.

Так как напряжённость электрического поля прямо пропорциональна разности потенциалов (U = Ed), то для энергии можно записать формулу

Энергия конденсатора прямо пропорциональна квадрату напряжённости электрического поля внутри его: W_п

Применение конденсаторов. Зависимость электроёмкости конденсатора от расстояния между его пластинами используется при создании одного из типов клавиатур компьютера. На тыльной стороне каждой клавиши располагается одна пластина конденсатора, а на плате, расположенной под клавишами, — другая. Нажатие клавиши изменяет ёмкость конденсатора. Электронная схема, подключённая к этому конденсатору, преобразует сигнал в соответствующий код, передаваемый в компьютер.

Энергия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, аккумуляторы в качестве источников электрической энергии. Но это совсем не означает, что конденсаторы как накопители энергии не получили практического применения. Конденсаторы могут накапливать энергию более или менее длительное время, а при разрядке через цепь с малым сопротивлением они отдают энергию почти мгновенно. Именно это свойство широко используют на практике.

Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заряжаемого предварительно специальной батареей. Возбуждение квантовых источников света — лазеров осуществляется с помощью газоразрядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроёмкости. Однако основное применение конденсаторы находят в радиотехнике.

Домашнее задание:
I. Учить §§ 97 – 98.
II. Ответить на вопросы:
1. Что называют электроёмкостью двух проводников?
2. Почему понятие электроёмкости неприменимо к диэлектрикам?
3. От чего зависит электроёмкость?
4. Как изменяется ёмкость конденсатора при наличии диэлектрика между его обкладками?
5. Какие существуют типы конденсаторов?
6. Какую роль выполняют конденсаторы в технике?

7.Чему равна энергия заряженного конденсатора?
8. Перечислите основные области применения конденсаторов.
III. Выполнить задание А1 – А2 на стр. 326
А1. Как изменится энергия электрического поля конденсатора, если заряд на его обкладках уменьшить в 2 раза?
1) не изменится; 3) уменьшится в 4 раза
2) уменьшится в 2 раза; 4) увеличится в 2 раза

А2. Конденсатор подключён к источнику постоянного напряжения. Как изменится энергия электрического поля внутри конденсатора, если увеличить в 2 раза расстояние между обкладками конденсатора?
1) не изменится; 3) уменьшится в 2 раза
2) увеличится в 2 раза; 4) правильный ответ не приведён

Электрическая емкость. Конденсаторы

Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.

Проводники и диэлектрики в электростатическом поле

Вещества в природе можно разделить на проводники и диэлектрики.

Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.

Типичные проводники — металлы.

Диэлектрическая проницаемость вещества

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

Физическая величина, равная отношению модуля напряженности (vec_0) внешнего электрического поля в вакууме к модулю напряженности (vec) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества (varepsilon) .

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:

Единицы измерения: (displaystyle [text<Ф>]) (фарад).

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.

Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами , а проводники, составляющие конденсатор, — обкладками .

Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Электроемкость плоского конденсатора

Разность потенциалов (Delta varphi) между пластинами в однородном электрическом поле равна (Ed) , где (d) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:

Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.

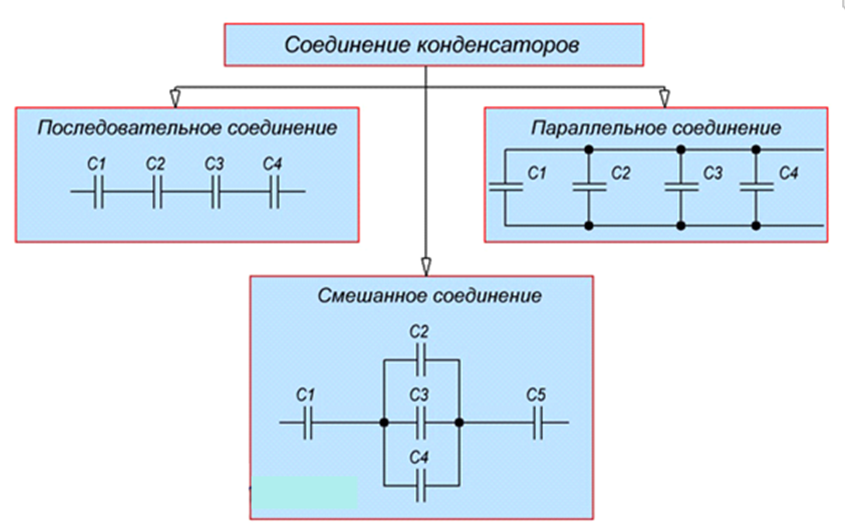
Последовательное и параллельное соединение конденсаторов

Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.

Последовательное соединение конденсаторов

При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах , но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.

Напряжение на данном участке цепи соотносятся следующим образом:

Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:

Сократив выражение на (Q) , получим формулу:

Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:

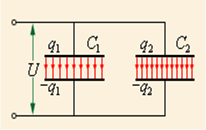
Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.

Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:

Так как заряд конденсатора

А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов

По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.

Вычислим эту энергию: начнём с плоского воздушного конденсатора.

Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора (q) , площадь обкладок (S) . Возьмём на второй обкладке настолько маленькую площадку, что заряд (q_0) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где (E_1) — напряжённость поля первой обкладки:

Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила (F) притяжения второй обкладки к первой складывается из всех этих сил (F_0) , с которыми притягиваются к первой обкладке всевозможные маленькие заряды (q_0) второй обкладки. При этом суммировании постоянный множитель (displaystyledfrac<2varepsilon_0S>) вынесется за скобку, а в скобке просуммируются все (q_0) и дадут (q) . В результате получим

Предположим теперь, что расстояние между обкладками изменилось от начальной величины (d_1) до конечной величины (d_2) . Сила притяжения пластин совершает при этом работу [A = F(d_1 -d_2)]

Знак правильный: если пластины сближаются ((d_2 , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины ((d_2 > d_1)) , то работа силы притяжения получается отрицательной, как и должно быть.

Это можно переписать следующим образом: [A =-(W_2-W_1) =-Delta W,]

Работа потенциальной силы (F) притяжения обкладок оказалась равна изменению со знаком минус величины (W) . Это как раз и означает, что (W) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение (q = CU) , можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).

Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Как изменяется емкость конденсатора при наличии диэлектрика

Электроемкость. Конденсаторы.

Выясним важный для практики вопрос: при каком условии можно накопить на проводниках большой электрический заряд?

При электризации двух проводников, например от электростатической машины, один из них приобретает заряд + q , а другой — q . Между проводниками появляется электрическое поле и возникает разность потенциалов (напряжение). С увеличением заряда проводников электрическое поле между ними усиливается.

Электроемкость проводников.

Введем физическую величину, характеризующую способность двух проводников накапливать электрический заряд. Эту величину называют электроемкостью.

Электроемкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между ними:

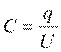
Электроемкость проводников тем больше, чем меньше разность потенциалов между ними при сообщении им зарядов противоположных знаков.

Единицу измерения электроемкости называют фарад (Ф); 1 Ф = 1 Кл/В.

Электроемкость — это скалярная величина

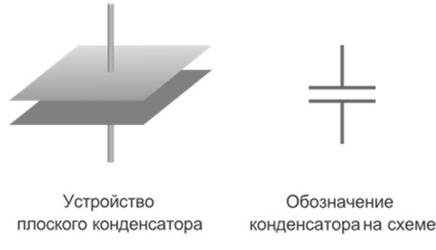
Плоский к онденсатор .

Большой электроемкостью обладают системы из двух проводников, называемые конденсаторами. Конденсатор представляет собой два проводника, ленные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники в этом случае называются обкладками конденсатора.

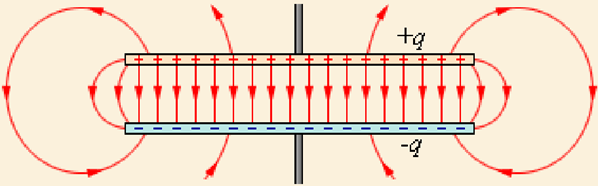
Если заряды пластин одинаковы по модулю и противоположны по знаку, то силовые линии электрического поля начинаются на положительно заряженной обкладке конденсатора и оканчиваются на отрицательно заряженной. Поэтому почти все электрическое поле сосредоточено внутри конденсатора и однородно.

Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника напряжения, например к полюсам батареи аккумуляторов. Можно также первую обкладку соединить с полюсом батареи, у которой другой полюс заземлен, а вторую обкладку конденсатора заземлить. Тогда на заземленной обкладке останется заряд, противоположный по знаку и равный по модулю заряду незаземленной обкладки. Такой же по модулю заряд уйдет в землю.

Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок.

Электроемкость плоского конденсатора.

Электроемкость конденсатора определяется формулой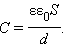

Электрические поля окружающих тел почти не проникают внутрь конденсатора и не влияют на разность потенциалов между его обкладками. Поэтому электроемкость конденсатора практически не зависит от наличия вблизи него каких-либо других тел.

Геометрия плоского конденсатора полностью определяется площадью S его пластин и расстоянием d между ними. От этих величин и должна зависеть емкость плоского конденсатора.

Кроме того, емкость конденсатора зависит от свойств диэлектрика между пластинами ε. Так как диэлектрик ослабляет поле, то электроемкость при наличии диэлектрика увеличивается.

Демонстрация зависимости электроемкости от параметров

Соединение конденсаторов

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов напряжения на конденсаторах одинаковы: U ₁ = U ₂ = U , а заряды равны q ₁ = С ₁ U и q ₂ = C ₂ U . Такую систему можно рассматривать как единый конденсатор электроемкости C , заряженный зарядом q = q ₁ + q ₂ при напряжении между обкладками равном U . Отсюда следует

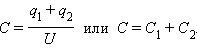
Последовательное соединение конденсаторов

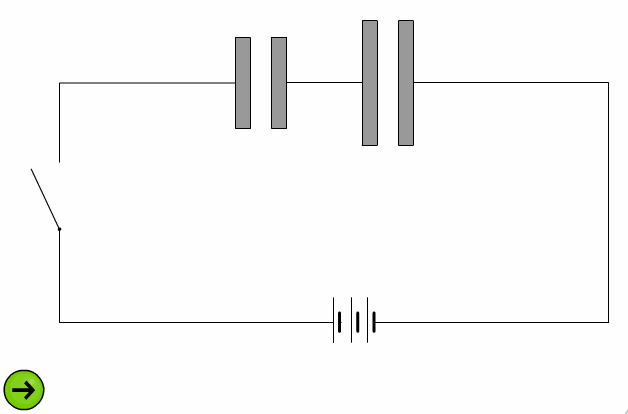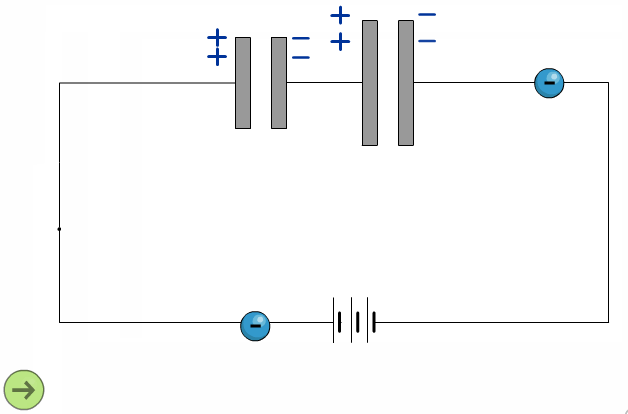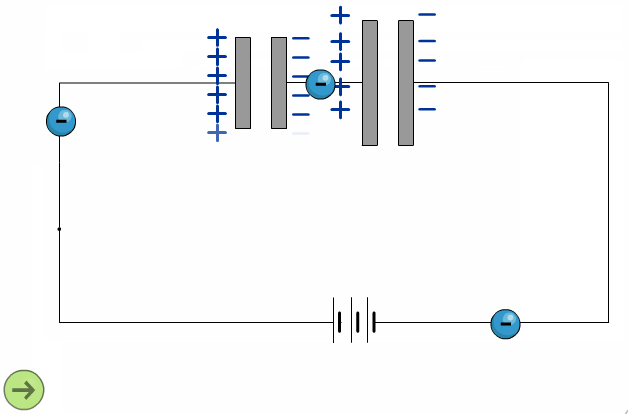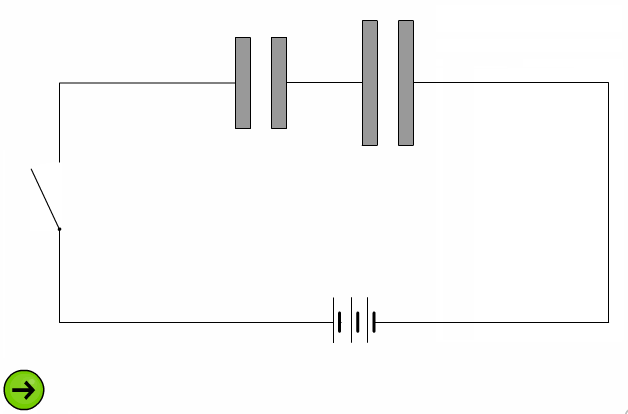
При последовательном соединении одинаковыми оказываются заряды обоих конденсаторов: q ₁ = q ₂ = q , а напряжения на них равны 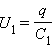и .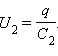

Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U ₁ + U ₂ . Следовательно, .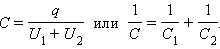

Или

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Энергия заряженного конденсатора:

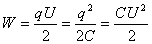
Применение конденсаторов:
— в компьютерной технике клавиатура (зависимость емкость от расстояние между пластинами). На тыльной стороне клавиши одна пластина конденсатора, а на плате – другая. Нажатие клавиши изменяет емкость конденсатора.
— в радиотехнике, в автоматизации производственных процессов, в вычислительной технике и т.д.
— в фототехнике.

Контрольные вопросы:

1. Что называют электроемкостью двух проводников?

2. В каких единицах выражается электроемкость?

3. От чего зависит электроемкость?

4. Как изменяется емкость конденсатора при наличии диэлектрика между его обкладками;

5. Какие существуют типы конденсаторов?

6. Какую роль выполняют конденсаторы в технике?

1. Определить заряд в плоском конденсаторе емкостью 0,02 мкФ, если напряженность поля в конденсаторе 320 В/см, а расстояние между пластинами 0,5 см. Каким будет напряжение, если зазор между пластинами увеличить в два раза?

2. Три конденсатора соединены, как показано на рисунке. Напряжение, подведенное между точками А и В равно 250 В, С₁=1,5мкФ, С₂— 3мк Ф, С₃ = 4 мкФ. Чему равна энергия трех конденсаторов.

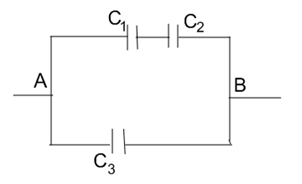
3. Три конденсатора с емкостями С₁=1мкФ, С₂= 1мк Ф, С₃ = 2 мкФ соединены по схеме и подключены к источнику постоянного напряжения 120В. Какова общая электроемкость. Определить заряд и напряжение на каждом конденсаторе.

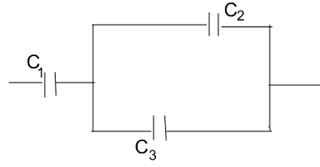
4. Электроемкость батареи конденсаторов равна 5,8 мкФ. Какова электроемкость и заряд первого конденсатора, если С₂= 1мк Ф, С₃ = 4 мкФ, а подведенное напряжение 220В?

5. Во сколько раз изменится емкость конденсатора при уменьшении рабочей площади пластин в 2 раза и уменьшении расстояния между ними в 3 раза?

Домашнее задание :

Составить план обобщенного характера изучения величины электроемкость.

1. Какое явление и свойство тел (веществ) характеризует данная величина.

2. Определение величины.

3. Определительная формула (для производной величины – формула, выражающая связь данной величины с другими).

4. Какая величина – скалярная или векторная.

5. Единица величины в СИ.

6. Способы измерения величины

1. Три последовательно соединенных конденсатора присоединены к источнику напряжения 32 В. Электроемкости конденсаторов равны соответственно 0,1; 0,25 и 0,5 мкФ. Определите напряжения на каждом конденсаторе.

2. Конденсатор электроемкостью 20 мкФ, заряженный до разности потенциалов 100 В, соединили параллельно с заряженным до разности потенциалов 40 В другим конденсатором, электроемкость которого неизвестна.

Образец решения задач.

Задача 1. Найти емкость С системы конденсаторов, изображенной на рисунке. Емкость каждого конденсатора C_i = 0,5 мкФ