Представление текстовой информации в памяти компьютера (1 час)
Для того чтобы сохранить на внешних носителях текстовый документ, созданный с помощью компьютера, он должен быть представлен двоичным кодом с помощью двух цифр – 0 и 1.
Посчитаем, сколько бит необходимо для кодирования одновременно:
- Символов типа № % * ? – (не менее 15)
- Букв латинского алфавита (строчных и прописных) – 52
- Букв кириллицы (русский алфавит) – 66
- Цифры – 10
Уже получилось 143 символа.
Чтобы закодировать такое количество символов необходимо не менее 8 бит (или 1 байт). Теперь мы знаем, что для кодирования одного символа требуется один байт информации. Итак, кодирование заключается в том, что каждому символу ставиться в соответствие уникальный двоичный код от 00000000 до 11111111 (или десятичный код от 0 до 255).
Важно, что присвоение символу конкретного кода – это вопрос соглашения, которое фиксируется кодовой таблицей. Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера (коды), называется таблицей кодировки.
Для разных типов ЭВМ используются различные кодировки. С распространением IBM PC международным стандартом стала таблица кодировки ASCII (American Standart Code for Information Interchange) – Американский стандартный код для информационного обмена. Стандартной в этой таблице является только первая половина, т.е. символы с номерами от 0 (00000000) до 127 (0111111). Сюда входят буква латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы.
Остальные 128 кодов используются в разных вариантах. Например, в русских кодировках размещаются символы русского алфавита.
Применим наши знания на практике, для чего рассмотрим, как будет представлено в памяти компьютера сообщение «stop». Для этого нам необходимы: кодовая таблица ASCII, знания о системах счисления и умение переводить числа из 10-ой системы счисления в двоичную.
Выпишем из кодовой таблицы десятичные коды соответствующих символов: Десятичный код 115 116 111 112
Переведем эти коды в двоичную систему и дополним слева нулями до 8-ми разрядной сетки: Двоичный 001110011 01110100 01101111 01110000
Задание: Закодировать в двоичной форме свои фамилию, имя, отчество, записанные латиницей, используя таблицу ASCII..
Информация в памяти компьютера имеет десятичную форму
©Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — авторский с подробными пояснениями профильными специалистами. Вы сможете скачать гдз, решебники, улучшить школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.
Тест по информатике Представление чисел в компьютере 10 класс
Тест по информатике Представление чисел в компьютере 10 класс с ответами. Тест включает 5 заданий с выбором ответа.
1. Определите представление в памяти компьютера числа 15710 в 8-разрядной ячейке памяти в формате «без знака».
1) 10111001
2) 01001110
3) 10011101
4) 01110101
2. Определите представление в памяти компьютера числа –10210 в 8-разрядной ячейке памяти в формате «со знаком».
1) 11100110
2) 10011010
3) 10011001
4) 01100110
3. Какое число получится, если сложить 8310 и 20410 в 8-битном формате без знака?
4. Для чисел 1.0125 × 10 1 и 1287.5 × 10 -2 найдите сумму, и представьте ее в нормализованном виде.
5. Для чисел 0.009625 × 10 3 и 6 найдите произведение, и представьте его в нормализованном виде.
Ответы на тест по информатике Представление чисел в компьютере 10 класс
1. 3
2. 2
3. 31
4. 2.3 × 10 1
5. 5.775 × 10 1
История науки и техники Com New
Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.
Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 – 1 = 255 = 11111111и минимальное 0 = 00000000. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255.
В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536 = 0000001000011000будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536 = 1000001000011000 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 – 1 = 2 – 1 = 2 – 1 = 32767 = 111111111111111 и диапазон чисел будет находиться в пределах от -32767 до 32767.
Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.
Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:
1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;
2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);
3) к полученному обратному коду прибавить единицу к младшему разряду.
Например, для числа -536 в таком формате модуль будет равен 0000001000011000, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536, т. е. число 536, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.
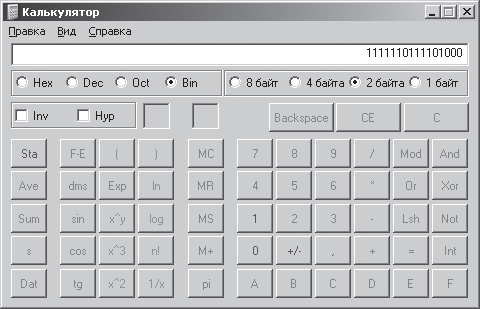
Рис. 2.6. Результат получения дополнительного кода
Необходимо помнить, что дополнительный код положительного числа – само число.
Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 – 1) … + 2 – 1 и -(2-1) … + 2 – 1.
Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).
Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.
Единицы измерения информации
Бит – минимальная единица измерения информации, количество информации, которым описывается состояние «включен» (1) или «выключен» (0). Слово «бит» произошло от Binary Digit (двоичная цифра). Именно такое определение единицы «бит» и дано выше в подразделе «Кодирование чисел». Есть ли электрическое напряжение на выводах схемы, есть ли электрический заряд в ячейке памяти, какое из двух возможных противоположных направлений намагниченности в данной области магнитного носителя, отражает ли свет лазерный оптический диск – все это вопросы, требующие ответа Да или Нет, один из которых трактуется как логическая единица, а второй – как логический нуль, поэтому электронный способ счета основан всего на двух цифрах, 0 и 1. Именно данные в формате этих цифр поручается хранить компьютерной памяти и обрабатывать вычислительной системе.
Байт – единица измерения количества информации, объема памяти и емкости запоминающего устройства. В памяти ЭВМ байт – наименьшая адресуемая единица данных, обрабатываемая как единое целое (в первых компьютерах за раз могло обрабатываться число длиной 8 бит), поэтому в качестве единицы измерения объема компьютерной информации выбрана более крупная, чем бит, единица информации – байт, последовательность 8 бит, т.е. 1 байт = 8 бит.
В символьных (текстовых) данных каждый символ кодируется (обозначается) одним байтом. Уникальное 8-битовое обозначение (код) получают заглавные и строчные буквы английского и русского алфавитов, цифры от 0 до 9, знаки препинания, другие символы (процент, номер) и некоторые управляющие коды передачи информации. На одной машинописной странице при размещении 50 строк и 60 символов текста в одной строке помещается 3 тыс. символов, следовательно, для хранения такого текста потребуется 3 тыс. байт машинной памяти.
Для записи чисел короче 8 бит в байтах добавляются слева нули (см. табл. 1.1). Левые нули не меняют двоичное число, но создают единую форму записи чисел – 8 бит на любое число от 0 до 255.
В десятичной системе счисления укрупненные единицы измерения обозначаются приставками к названию кило, Мега, Гига, что соответствует увеличению численного значения на множитель десять в степени: 103 = 1000 (тысяча), 106 = 1 000 000 (миллион), 109= 1 000 000 000 (миллиард), т.е. переход к следующей, более крупной, единице сопровождается умножением па 1000 (103). В двоичной системе укрупненные единицы измерения тоже обозначаются приставками к названию кило, Мега, Гига, Тера, Пета, Экза, но они увеличивают численное значение на множитель 2 в степени: 210, 220, 230, 240, 250, 260, т.е. переход к следующей, более крупной, единице сопровождается умножением на 210 = 1024:
- • 1 Кбайт = 1024 байт = 210 байт;
- • 1 Мбайт = 1024 Кбайт = 220 байт;
- • 1 Гбайт = 1024 Мбайт = 230 байт;
- • 1 Тбайт = 1024 Гбайт = 240 байт;
- • 1 Пбайт = 1024 Гбайт = 250 байт;
- • 1 Эбайт = 1024 Пбайт = 260 байт.
Передача информации по каналам связи характеризуется скоростью передачи данных: бит в секунду, Кбит/с, Мбит/с и др. Количество переданных бит удобнее считать в десятичной системе счисления, поэтому приставки в единицах измерения скорости связаны коэффициентом 1000 (103). Единица измерения скорости передачи данных 1 бит/с называется бодом.