Иерархические структуры данных в реляционных БД
Архитектура реляционных баз данных ориентирована на хранение внутри таблиц БД информации о сущностях информационной системы и связях между ними. Каждая из записей таблицы содержит информацию об одном экземпляре. Организация хранения информации о независимых друг от друга экземплярах сущностей (т.е. так называемых «плоских» данных) не вызывает никаких затруднений. Однако, наряду с «плоскими» данными, при построении даже простых информационных систем, приходится хранить в БД и информацию о «вложенных» друг в друга сущностях, т.е иерархические данные. Организация хранения такой информации в реляционных БД проста, но не всегда очевидна для тех, кто впервые сталкивается с подобной задачей. В данной статье я попытаюсь поделиться накопленным опытом.
Примеры, приводимые далее, были созданы и протестированы с помощью Interbase 6.
Иерархии данных
Чтобы обсудить проблему хранения иерархии в реляционной БД, мы вначале рассмотрим вопрос о том, какие же иерархии данных могут встретиться на практике. В реальной жизни иерархии имеют, как правило, некоторые ограничения. Учитывая эти ограничения, можно построить более эффективные процедуры обработки иерархических данных.
Так, в общем случае, дерево может иметь любое количество уровней иерархии. Но в частных случаях число уровней может, и часто оказывается, конечным. Может быть ограничено количество непосредственных потомков одного элемента иерархии.
Рассмотрим некоторые варианты представления иерархических структур в реляционных БД.
Возможные варианты структур БД для хранения иерархий
Наиболее общим случаем является дерево с неограниченным уровнем вложенности и неограниченным количеством потомков. Для хранения такого рода иерархии необходимо добавить в описание сущности дополнительное поле – ссылку на первичный ключ предка. Такой способ организации иерархии является самым распространенным и универсальным. Однако ему присущи следующие недостатки:
Необходимость рекурсивных запросов для получения полного пути от произвольного элемента до корня дерева.
Сложность вычисления уровня вложенности произвольного элемента.
Сложность получения всех (в том числе и не прямых) потомков данного узла.
Дальнейшее рассмотрение мы будем вести на примере построения иерархической структуры – тематического каталога библиотеки. Данный каталог применяется для классификации, сортировки и поиска книг по их содержанию. Будем считать, что каждый элемент каталога описывается собственным неуникальным символьным именем. Для обеспечения уникальности записей для каждого элемента каталога необходимо ввести первичный ключ. Для поддержки иерархичности данных введем дополнительное поле-ссылку на предка данного элемента иерархии. Ниже приведено описание полученной структуры на языке SQL:
Данная структура является минимально необходимой и достаточной для организации и хранения иерархии. Назовем ее структурой со ссылкой на предка . В данной структуре присутствует как минимум один недостаток – отсутствие контроля правильности ссылки на родителя. Какие же значения поля PARENT_ID являются правильными? Ответ очевиден – весь диапазон значений первичного ключа (поля ID) + одно значение, используемое для обозначения отсутствия родительского элемента. Данное значение необходимо для ввода и хранения корневых элементов иерархии. Чаще всего в качестве значения, обозначающего отсутствие родителя, используется NULL, хотя нет никаких физических ограничений для использования других значений. Так, например, если вы уверены, что значения первичного ключа будут больше 0, в качестве признака корневого элемента можно использовать значение (–1) или другие отрицательные значения в поле PARENT_ID. Я не буду оригинален и в качестве значения PARENT_ID для корневых элементов использую NULL. Тогда для контроля правильности PARENT_ID можно использовать следующее ограничение:
Вернемся к отмеченным выше недостаткам данной структуры (сложность формирования полного пути и вычисления уровня элемента). Эти недостатки вытекают из того простого факта, что в данной структуре информация о полном пути и уровне нигде не хранится. Решить проблему быстрого получения уровня вложенности можно введением в структуру таблицы дополнительного поля Level. Описание таблицы тогда будет выглядеть так:
Структура для хранения иерархии с неограниченным числом уровней вложенности и потомков готова.
Следующей по степени универсальности является иерархия с неограниченным числом уровней вложенности и конечным числом потомков элемента иерархии. Ограничение количества потомков позволяет хранить данные в следующем виде.
- Ссылка на предка
- Информация о первом элементе уровня иерархии
- Информация о втором элементе уровня иерархии
- …
- Информация о n-ном элементе уровня иерархии, где n – количество максимальное количество потомков
Ссылка на предка содержит в себе ссылку на запись, хранящую информацию о предыдущем уровне иерархии и смещение (номер столбца) с описанием родителя.
В нашем примере мы ограничим количество предков числом 5, тогда SQL-описание таблицы будет выглядеть следующим образом:
Больших преимуществ использования такой структуры я не вижу, недостаток же налицо – при изменении максимального количества потомков одного узла придется добавлять еще один столбец таблицы, что крайне неудобно. По этой причине подробно рассматривать эту структуру мы не станем, а перейдем к следующему случаю – иерархии с конечным числом уровней вложенности и бесконечным числом потомков узла.
Одним из вариантов хранения таких иерархий является поуровневое хранение в различных таблицах. Например, таблица CATALOG_LEVEL_1 хранит все элементы первого уровня вложенности, таблица CATALOG_LEVEL_2 – второго, и т.д. Ниже приведено описание такой структуры для случая трехуровневой иерархии.
При большем количестве уровней необходимо определить дополнительные таблицы для каждого уровня, по структуре аналогичные таблице CATALOG3_LEVEL2. В данной структуре получение уровня элемента не представляет никакой сложности, т.к однозначно определяется таблицей, в которой он хранится. Полный путь от любого элемента до корня также определяется составным первичным ключом таблицы. Этот вид структуры назовем структурой с потабличным хранением уровней
Последний из видов иерархии – иерархия с ограниченной вложенностью и ограниченным числом потомков. Многие из реальных задач, встречавшихся мне, в той или иной степени можно было свести к этому виду иерархии. Так, например, наша задача с каталогом библиотеки, хотя в строгом виде и является иерархией с неограниченным числом потомков узла и вложенностью, может быть сведена к рассматриваемому типу иерархии. Вполне можно ограничить количество элементов на одном уровне значением 9 (или другим достаточно большим числом) и 5 уровнями вложенности. Зачем? Затем, что в данном типе иерархии при определенной организации первичного ключа можно существенно упростить работу с иерархией. Для хранения данного вида иерархии можно использовать ранее описанные структуры иерархий с неограниченной вложенностью и количеством потомков и иерархий с ограниченным количеством уровней и неограниченным числом потомков. Однако есть две модификации структур специфичных для данного типа иерархии.
Первый тип приведен ниже:
Весь фокус в принципе формирования первичного ключа ID. Позиция последнего ненулевого десятичного разряда ключа – это уровень элемента, а цифра в этой позиции – номер элемента на данном уровне. Например, первый элемент первого уровня будет иметь второй – 00002. На втором уровне третий элемент, имеющий предком первый элемент первого уровня, будет иметь и т.д. Данная структура хороша при равномерном распределении элементов по уровням. Ее мы назовем структурой с поразрядным ключом . В зависимости от того, справа или слева находится разряд, кодирующий первый уровень, можно выделить структуру с поразрядным правым ключом и структуру с поразрядным левым ключом . В нашем случае я описал правый ключ. Если же максимальное число элементов конечно, но различно для различных ветвей дерева, и хотя бы приблизительно может быть оценено для каждой ветви, можно воспользоваться следующей структурой:
Данная структура является модификацией структуры для хранения иерархии с неограниченным уровнем вложенности и количеством потомков. В структуру добавлены поля LOW и HIGH для хранения начала и конца диапазона первичных ключей всех потомков данного элемента. Такая иерархия может быть представлена набором отрезков (см. рисунок). Это позволяет быстро и легко выбрать всех потомков данного элемента. Данную структуру назовем структурой с хранением границ ветви .

Итак, мы рассмотрели несколько различных типов структур для хранения иерархий. Далее мы рассмотрим решение задач, связанных с использованием этих структур:
- получения потомков элемента;
- получения уровня вложенности элемента;
- получения полного пути от элемента до корня иерархии;
- операции вставки, удаления, перемещения элемента и его потомков для вышеперечисленных структур.
Получение непосредственных потомков
Получение потомков элемента является основной задачей при построении и отображении дерева. Далее мы рассмотрим получение потомков для:
структур со ссылкой на предка
К этому виду структур относится и модификация с поддержкой информации об уровне элемента, а также структура с хранением границ ветви. Очевидно, что в такой структуре потомками элемента будут все элементы, ссылающиеся на данный (PARENT_ID потомков равен ID родителя). Запрос на выборку потомков (имена таблицы и полей взяты из приведенных выше описаний) выглядит так:
структур с потабличным хранением уровней
В данной структуре для определения потомков необходимо знать уровень вложенности предка. Зная уровень вложенности, можно определить имя таблицы, в которой хранится информация о потомках. Запрос на выборку потомков:
Например, для определения потомков узла второго уровня с и PARENT_ID = 5 запрос будет:
структур с поразрядным ключом
При структуре с поразрядным правым ключом непосредственные потомки имеют первичные ключи c ненулевым следующим разрядом и таким же, как первичный ключ предка числом в младших разрядах. В ранее рассмотренном нами случае потомки первого корневого элемента (ID = 1) будут иметь ID 11,21,31,41, …91. Запрос на выборку:
SELECT “ID” FROM “CATALOG4” WHERE “ID” IN (11,21,31,41,51,61,71,81,91)
Структура с левым ключом для первого корневого элемента (ID = 10000) потомки 11000, 12000,13000…19000.
Получение всех потомков
Довольно часто возникает задача получения всех, в том числе и не прямых потомков данного элемента. Рассмотрим решение этой задачи для приведенных структур.
структура со ссылкой на предка и ее модификация с поддержкой информации об уровне элемента
Простого способа, к сожалению, нет. Приходится организовывать рекурсию запросов.
структура с потабличным хранением уровней
Потомки данного элемента содержатся в “нижележащих” таблицах и имеют как часть составной ссылки на предка в одном из полей значение ID предка. Общий список потомков можно получить объединением (UNION) запросов.
Ввод дополнительного поля LEVEL в запрос обусловлен тем, что потомки элемента в разных таблицах могут иметь одинаковые ID и при объединении запросов вместо нескольких строк в результате будет получена одна. Еще одна проблема, приводящая к необходимости ввода дополнительного поля в запрос, т.к. надо знать, из какой таблицы выбран данный ID.
структура с поразрядным ключом
В данной структуре содержится информация о полном пути к элементу. Это облегчает выборку всех потомков.
Левый ключ
Для первого корневого элемента диапазон ID потомков будет 10001… 19999, для второго 20001…29999 и т.д.
Правый ключ
Ну, здесь тоже все просто. Первый элемент иерархии на втором уровне его первый предок 11 и т.д. Таким образом, потомки будут иметь в конце ID цифры, совпадающие с ID предка.
структура с хранением границ ветви
Элементы структуры LOW и HIGH хранят границы диапазона первичных ключей всех потомков.
Получения уровня вложенности элемента
Часто уровень вложенности элемента иерархии привязан к какому-либо классификационному признаку предметной области. Отсюда возникает задача определения уровня вложенности произвольного элемента.
структура со ссылкой на предка, структура с хранением границ ветви
Построение полного пути к корню дерева и определение числа предков. Довольно неудобно, но другого способа нет.
структура со ссылкой на предка и хранением уровня вложенности
Недаром мы ввели поле для хранения уровня вложенности. Оно-то и содержит нужную нам информацию.
структура с потабличным хранением уровней
Уровень вложенности определяется таблицей, в которой хранится запись об элементе.
структура с поразрядным ключом
Уровень вложенности определяется положением последнего ненулевого разряда в ключе.
Получения полного пути от элемента до корня иерархии
структура со ссылкой на предка и ее модификация с поддержкой информации об уровне элемента, структура с хранением границ ветви
Опять же, для вычисления полного пути нужно получать предков с помощью последовательных запросов. Одним простым запросом здесь не обойтись. Ниже приведен текст хранимой процедуры получения полного пути от произвольного элемента:
структура с потабличным хранением уровней, структура с поразрядным ключом
Полный путь содержится в первичном ключе элемента.
Операции вставки, удаления, перемещения элемента и его потомков
структура со ссылкой на предка
Добавление нового элемента:
Удаление элемента: Кроме непосредственно самого элемента необходимо удалить и его потомков. Проблема решается введением триггера:
Перемещение элемента: надо просто поменять ссылку на родителя.
структура со ссылкой на предка и поддержкой уровней
Можно использовать запросы, аналогичные случаю с базовой структурой. Для проверки корректности поля Level можно ввести дополнительные триггеры:
структура с потабличным хранением уровней
Запросы на вставку и перемещения тривиальны, и потому не приводятся. При удалении элемента можно ввести дополнительный триггер для удаления потомков, аналогично триггеру для структуры со ссылкой на предка.
структура с хранением границ ветви
Вставка и удаление аналогичны случаю структуры со ссылкой на предка. Перемещение элемента в общем случае невозможно без перегенерации первичных ключей элементов, поэтому применяется редко.
Заключение
Ну вот, пожалуй, и все. Надеюсь, что данная статья будет вам полезна. Если у вас появились замечания, предложения или Вы обнаружили какие-либо ошибки, пишите мне mgoblin@mail.ru
Иерархические структуры данных в реляционных БД
Архитектура реляционных баз данных ориентирована на хранение внутри таблиц БД информации о сущностях информационной системы и связях между ними. Каждая из записей таблицы содержит информацию об одном экземпляре. Организация хранения информации о независимых друг от друга экземплярах сущностей (т.е. так называемых «плоских» данных) не вызывает никаких затруднений. Однако, наряду с «плоскими» данными, при построении даже простых информационных систем, приходится хранить в БД и информацию о «вложенных» друг в друга сущностях, т.е иерархические данные. Организация хранения такой информации в реляционных БД проста, но не всегда очевидна для тех, кто впервые сталкивается с подобной задачей. В данной статье я попытаюсь поделиться накопленным опытом.
Примеры, приводимые далее, были созданы и протестированы с помощью Interbase 6.
Иерархии данных
Чтобы обсудить проблему хранения иерархии в реляционной БД, мы вначале рассмотрим вопрос о том, какие же иерархии данных могут встретиться на практике. В реальной жизни иерархии имеют, как правило, некоторые ограничения. Учитывая эти ограничения, можно построить более эффективные процедуры обработки иерархических данных.
Так, в общем случае, дерево может иметь любое количество уровней иерархии. Но в частных случаях число уровней может, и часто оказывается, конечным. Может быть ограничено количество непосредственных потомков одного элемента иерархии.
Рассмотрим некоторые варианты представления иерархических структур в реляционных БД.
Возможные варианты структур БД для хранения иерархий
Наиболее общим случаем является дерево с неограниченным уровнем вложенности и неограниченным количеством потомков. Для хранения такого рода иерархии необходимо добавить в описание сущности дополнительное поле — ссылку на первичный ключ предка. Такой способ организации иерархии является самым распространенным и универсальным. Однако ему присущи следующие недостатки:
Необходимость рекурсивных запросов для получения полного пути от произвольного элемента до корня дерева.
Сложность вычисления уровня вложенности произвольного элемента.
Сложность получения всех (в том числе и не прямых) потомков данного узла.
Дальнейшее рассмотрение мы будем вести на примере построения иерархической структуры — тематического каталога библиотеки. Данный каталог применяется для классификации, сортировки и поиска книг по их содержанию. Будем считать, что каждый элемент каталога описывается собственным неуникальным символьным именем. Для обеспечения уникальности записей для каждого элемента каталога необходимо ввести первичный ключ. Для поддержки иерархичности данных введем дополнительное поле-ссылку на предка данного элемента иерархии. Ниже приведено описание полученной структуры на языке SQL:
Данная структура является минимально необходимой и достаточной для организации и хранения иерархии. Назовем ее структурой со ссылкой на предка . В данной структуре присутствует как минимум один недостаток — отсутствие контроля правильности ссылки на родителя. Какие же значения поля PARENT_ID являются правильными? Ответ очевиден — весь диапазон значений первичного ключа (поля ID) + одно значение, используемое для обозначения отсутствия родительского элемента. Данное значение необходимо для ввода и хранения корневых элементов иерархии. Чаще всего в качестве значения, обозначающего отсутствие родителя, используется NULL, хотя нет никаких физических ограничений для использования других значений. Так, например, если вы уверены, что значения первичного ключа будут больше 0, в качестве признака корневого элемента можно использовать значение (-1) или другие отрицательные значения в поле PARENT_ID. Я не буду оригинален и в качестве значения PARENT_ID для корневых элементов использую NULL. Тогда для контроля правильности PARENT_ID можно использовать следующее ограничение:
Вернемся к отмеченным выше недостаткам данной структуры (сложность формирования полного пути и вычисления уровня элемента). Эти недостатки вытекают из того простого факта, что в данной структуре информация о полном пути и уровне нигде не хранится. Решить проблему быстрого получения уровня вложенности можно введением в структуру таблицы дополнительного поля Level. Описание таблицы тогда будет выглядеть так:
Структура для хранения иерархии с неограниченным числом уровней вложенности и потомков готова.
Следующей по степени универсальности является иерархия с неограниченным числом уровней вложенности и конечным числом потомков элемента иерархии. Ограничение количества потомков позволяет хранить данные в следующем виде.
- Ссылка на предка
- Информация о первом элементе уровня иерархии
- Информация о втором элементе уровня иерархии
- .
- Информация о n-ном элементе уровня иерархии, где n — количество максимальное количество потомков
Ссылка на предка содержит в себе ссылку на запись, хранящую информацию о предыдущем уровне иерархии и смещение (номер столбца) с описанием родителя.
В нашем примере мы ограничим количество предков числом 5, тогда SQL-описание таблицы будет выглядеть следующим образом:
Больших преимуществ использования такой структуры я не вижу, недостаток же налицо — при изменении максимального количества потомков одного узла придется добавлять еще один столбец таблицы, что крайне неудобно. По этой причине подробно рассматривать эту структуру мы не станем, а перейдем к следующему случаю — иерархии с конечным числом уровней вложенности и бесконечным числом потомков узла.
Одним из вариантов хранения таких иерархий является поуровневое хранение в различных таблицах. Например, таблица CATALOG_LEVEL_1 хранит все элементы первого уровня вложенности, таблица CATALOG_LEVEL_2 — второго, и т.д. Ниже приведено описание такой структуры для случая трехуровневой иерархии.
При большем количестве уровней необходимо определить дополнительные таблицы для каждого уровня, по структуре аналогичные таблице CATALOG3_LEVEL2. В данной структуре получение уровня элемента не представляет никакой сложности, т.к однозначно определяется таблицей, в которой он хранится. Полный путь от любого элемента до корня также определяется составным первичным ключом таблицы. Этот вид структуры назовем структурой с потабличным хранением уровней
Последний из видов иерархии — иерархия с ограниченной вложенностью и ограниченным числом потомков. Многие из реальных задач, встречавшихся мне, в той или иной степени можно было свести к этому виду иерархии. Так, например, наша задача с каталогом библиотеки, хотя в строгом виде и является иерархией с неограниченным числом потомков узла и вложенностью, может быть сведена к рассматриваемому типу иерархии. Вполне можно ограничить количество элементов на одном уровне значением 9 (или другим достаточно большим числом) и 5 уровнями вложенности. Зачем? Затем, что в данном типе иерархии при определенной организации первичного ключа можно существенно упростить работу с иерархией. Для хранения данного вида иерархии можно использовать ранее описанные структуры иерархий с неограниченной вложенностью и количеством потомков и иерархий с ограниченным количеством уровней и неограниченным числом потомков. Однако есть две модификации структур специфичных для данного типа иерархии.
Первый тип приведен ниже:
Весь фокус в принципе формирования первичного ключа ID. Позиция последнего ненулевого десятичного разряда ключа — это уровень элемента, а цифра в этой позиции — номер элемента на данном уровне. Например, первый элемент первого уровня будет иметь второй — 00002. На втором уровне третий элемент, имеющий предком первый элемент первого уровня, будет иметь и т.д. Данная структура хороша при равномерном распределении элементов по уровням. Ее мы назовем структурой с поразрядным ключом . В зависимости от того, справа или слева находится разряд, кодирующий первый уровень, можно выделить структуру с поразрядным правым ключом и структуру с поразрядным левым ключом . В нашем случае я описал правый ключ. Если же максимальное число элементов конечно, но различно для различных ветвей дерева, и хотя бы приблизительно может быть оценено для каждой ветви, можно воспользоваться следующей структурой:
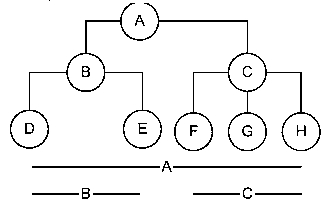
Данная структура является модификацией структуры для хранения иерархии с неограниченным уровнем вложенности и количеством потомков. В структуру добавлены поля LOW и HIGH для хранения начала и конца диапазона первичных ключей всех потомков данного элемента. Такая иерархия может быть представлена набором отрезков (см. рисунок). Это позволяет быстро и легко выбрать всех потомков данного элемента. Данную структуру назовем структурой с хранением границ ветви .
Итак, мы рассмотрели несколько различных типов структур для хранения иерархий. Далее мы рассмотрим решение задач, связанных с использованием этих структур:
- получения потомков элемента;
- получения уровня вложенности элемента;
- получения полного пути от элемента до корня иерархии;
- операции вставки, удаления, перемещения элемента и его потомков для вышеперечисленных структур.
Получение непосредственных потомков
Получение потомков элемента является основной задачей при построении и отображении дерева. Далее мы рассмотрим получение потомков для:
структур со ссылкой на предка
К этому виду структур относится и модификация с поддержкой информации об уровне элемента, а также структура с хранением границ ветви. Очевидно, что в такой структуре потомками элемента будут все элементы, ссылающиеся на данный (PARENT_ID потомков равен ID родителя). Запрос на выборку потомков (имена таблицы и полей взяты из приведенных выше описаний) выглядит так:
структур с потабличным хранением уровней
В данной структуре для определения потомков необходимо знать уровень вложенности предка. Зная уровень вложенности, можно определить имя таблицы, в которой хранится информация о потомках. Запрос на выборку потомков:
Например, для определения потомков узла второго уровня с и PARENT_ID = 5 запрос будет:
структур с поразрядным ключом
При структуре с поразрядным правым ключом непосредственные потомки имеют первичные ключи c ненулевым следующим разрядом и таким же, как первичный ключ предка числом в младших разрядах. В ранее рассмотренном нами случае потомки первого корневого элемента (ID = 1) будут иметь ID 11,21,31,41, .91. Запрос на выборку:
SELECT «ID» FROM «CATALOG4» WHERE «ID» IN (11,21,31,41,51,61,71,81,91)
Структура с левым ключом для первого корневого элемента (ID = 10000) потомки 11000, 12000,13000.19000.
Получение всех потомков
Довольно часто возникает задача получения всех, в том числе и не прямых потомков данного элемента. Рассмотрим решение этой задачи для приведенных структур.
структура со ссылкой на предка и ее модификация с поддержкой информации об уровне элемента
Простого способа, к сожалению, нет. Приходится организовывать рекурсию запросов.
структура с потабличным хранением уровней
Потомки данного элемента содержатся в «нижележащих» таблицах и имеют как часть составной ссылки на предка в одном из полей значение ID предка. Общий список потомков можно получить объединением (UNION) запросов.
Ввод дополнительного поля LEVEL в запрос обусловлен тем, что потомки элемента в разных таблицах могут иметь одинаковые ID и при объединении запросов вместо нескольких строк в результате будет получена одна. Еще одна проблема, приводящая к необходимости ввода дополнительного поля в запрос, т.к. надо знать, из какой таблицы выбран данный ID.
структура с поразрядным ключом
В данной структуре содержится информация о полном пути к элементу. Это облегчает выборку всех потомков.
Левый ключ
Для первого корневого элемента диапазон ID потомков будет 10001. 19999, для второго 20001.29999 и т.д.
Правый ключ
Ну, здесь тоже все просто. Первый элемент иерархии на втором уровне его первый предок 11 и т.д. Таким образом, потомки будут иметь в конце ID цифры, совпадающие с ID предка.
структура с хранением границ ветви
Элементы структуры LOW и HIGH хранят границы диапазона первичных ключей всех потомков.
Получения уровня вложенности элемента
Часто уровень вложенности элемента иерархии привязан к какому-либо классификационному признаку предметной области. Отсюда возникает задача определения уровня вложенности произвольного элемента.
структура со ссылкой на предка, структура с хранением границ ветви
Построение полного пути к корню дерева и определение числа предков. Довольно неудобно, но другого способа нет.
структура со ссылкой на предка и хранением уровня вложенности
Недаром мы ввели поле для хранения уровня вложенности. Оно-то и содержит нужную нам информацию.
структура с потабличным хранением уровней
Уровень вложенности определяется таблицей, в которой хранится запись об элементе.
структура с поразрядным ключом
Уровень вложенности определяется положением последнего ненулевого разряда в ключе.
Получения полного пути от элемента до корня иерархии
структура со ссылкой на предка и ее модификация с поддержкой информации об уровне элемента, структура с хранением границ ветви
Опять же, для вычисления полного пути нужно получать предков с помощью последовательных запросов. Одним простым запросом здесь не обойтись. Ниже приведен текст хранимой процедуры получения полного пути от произвольного элемента:
структура с потабличным хранением уровней, структура с поразрядным ключом
Полный путь содержится в первичном ключе элемента.
Операции вставки, удаления, перемещения элемента и его потомков
структура со ссылкой на предка
Добавление нового элемента:
Удаление элемента: Кроме непосредственно самого элемента необходимо удалить и его потомков. Проблема решается введением триггера:
Перемещение элемента: надо просто поменять ссылку на родителя.
структура со ссылкой на предка и поддержкой уровней
Можно использовать запросы, аналогичные случаю с базовой структурой. Для проверки корректности поля Level можно ввести дополнительные триггеры:
структура с потабличным хранением уровней
Запросы на вставку и перемещения тривиальны, и потому не приводятся. При удалении элемента можно ввести дополнительный триггер для удаления потомков, аналогично триггеру для структуры со ссылкой на предка.
структура с хранением границ ветви
Вставка и удаление аналогичны случаю структуры со ссылкой на предка. Перемещение элемента в общем случае невозможно без перегенерации первичных ключей элементов, поэтому применяется редко.
Заключение
Ну вот, пожалуй, и все. Надеюсь, что данная статья будет вам полезна. Если у вас появились замечания, предложения или Вы обнаружили какие-либо ошибки, пишите мне mgoblin@mail.ru












