Системы счисления, используемые в компьютере
Основные принципы устройства и работы компьютера были сформулированы в 1945 г. американским математиком Джоном фон Нейманом. Согласно этим принципам, машина должна использовать двоичную систему счисления, выполнять команды последовательно, одну за другой, и состоять из:
Важная особенность в архитектуре машины фон Неймана: команды и данные хранятся в памяти, причем в разные моменты времени в одном и том же месте памяти могут храниться и данные, и команды.
Память компьютера состоит из некоторого количества пронумерованных (имеющих свой адрес) ячеек, в каждой из которых могут находиться или обрабатываемые данные, или инструкции (команды) программ. Все ячейки памяти должны быть одинаково легко доступны для других устройств.
В общих чертах работа компьютера состоит в следующем: с какого-то внешнего устройства в память компьютера вводится программа – последовательность инструкций (команд). Устройство управления считывает из ячейки памяти первую инструкцию программы и организует ее выполнение с помощью арифметико-логического устройства. Эта команда может задавать выполнение каких-либо вычислений, чтение данных из памяти для выполнения операций или запись результатов в память, ввод данных с внешнего устройства в память или вывод данных из памяти на внешнее устройство. Затем выполняется следующая команда и т.д. Устройство управления выполняет команды автоматически, без вмешательства человека. Оно обменивается информацией с памятью компьютера и внешними устройствами. Результаты выполненной программы выводятся на внешние устройства компьютера.
В современных компьютерах устройство управления и арифметико-логическое устройство объединены в единое устройство – центральный процессор.
Системы счисления, используемые в компьютере
В компьютерах используется двоичная система счисления. Она оказалась наиболее простой для аппаратной реализации: естественным электронным способом счета является система, основанная на двух значениях – «нет сигнала/ есть сигнал». Если числа в десятичной системе записываются с помощью цифр от 0 до 9, то в двоичной – с помощью цифр 0 и 1. Информация любого типа может быть закодирована с использованием двух цифр.
В десятичной системе – 250=2•102+5•101+0•100
11=1•101+1•100
В двоичной системе – 10=1•21+0•20 = 2 в 10-ной системе
101=1•22+0•21+1•20 = (4+0+1)=5 в 10-ной системе.
Для обозначения адресов ячеек памяти и других целей удобнее пользоваться не двоичной, а более компактной шестнадцатиричной системой счисления, в которой двоичные цифры группируются по 4, и каждая такая группа, или тетрада, обозначается одним символом или шестнадцатиричной цифрой. В качестве цифр в шестнадцатиричной системе используются десять цифр обычной десятичной системы от 0 до 9 и шесть латинских букв от A до F (A – 10, B – 11, C – 12, D – 13, E – 14, F –15). При написании шестнадцатиричных цифр иногда используют символ h в конце числа.
Например, Ah=1•161+10•160=(16+10)=26 в десятичной системе
D4Fh=13•162+4•161+15•160=(3328+64+15)=3407 в десятичной.
2. Арифметические операции над числами, представленными в различных системах счисления
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно преобразовать их в одну систему счисления и учесть то, что перенос в следующий разряд при операции сложения и заем из старшего разряда при операции вычитания определяется величиной основания системы счисления.
Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.
При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице «Вычитание» этот заем обозначен 1 с чертой над цифрой.

Ниже приведены примеры выполнения арифметических операций над числами, представленными в различных системах счисления:
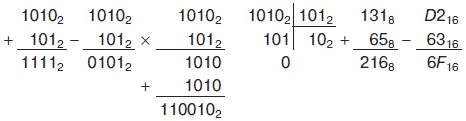
Арифметические операции над целыми числами, представленными в различных системах счисления, достаточно просто реализуются с помощью программ Калькулятор и MS Excel.
Системы счисления, используемые в компьютере
В компьютере используют двоичную систему счисления для Представления информации, потому что она имеет ряд преимуществ перед другими системами счисления:
• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (а не с десятью, как в десятичной системе счисления). Например: электромагнитное реле (замкнуто/ разомкнуто), которое широко использовалось в конструкциях первых ЭВМ; участок поверхности магнитного носителя информации (намагничен/размагничен); участок поверхности лазерного диска (отражает/не отражает); триггер, который может устойчиво находиться в одном из двух состояний;
• широко используется в оперативной памяти компьютера;
• представление информации посредством только двух состояний надежно и помехоустойчиво;
• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации (см. гл. 3);
• двоичная арифметика намного проще десятичной.
Недостаток двоичной системы счисления — быстрый рост числа
разрядов, необходимых для записи чисел.
Человеку очень трудно воспринимать многоразрядные числа, т.е. числа, записанные в двоичном коде, а для компьютера разрядность числа не имеет большого значения, так как современные компьютеры обрабатывают за один такт работы процессора более 64 двоичных разрядов.
Перевод чисел из десятичной системы счисления в двоичную и наоборот выполняет машина, однако программисты часто используют восьмеричную и шестнадцатеричную системы счисления на этапах отладки программ и просмотра содержимого файлов в режиме машинных кодов.
Числа в этих системах счисления читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе счисления (числа 8 и 16 — соответственно третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления очень прост; достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) Для восьмеричной системы счисления или тетрадой (четверкой Цифр) для шестнадцатеричной системы счисления.
Примеры.
5 3 7 1 1 А 3 F
Чтобы перевести число из двоичной системы счисления в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады или тетрады и каждую такую группу заменить соответствующей восьмеричной или шестнадцатери-чной цифрой.
Примеры.
10101001, 101112 = 10 101 001, 101 1112 = 251,568; 2 5 1 5 6
10101001, 101112 = Ю10 1001, 1011, 10002=Л9, Я816.
А 9 В 8
Арифметические операции в позиционных системах счисления
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только нужно пользоваться особыми для каждой системы таблицами сложения и умножения.
Сложение.При сложении цифры суммируются по разрядам; если при этом возникает избыток, то он переносится влево в старший разряд.
Сложение в двоичной системе счисления
Примеры.
Сложение в десятичной системе счисления: 1510+ 610.
Сложение в двоичной системе счисления: 11112+ 110:
Рассмотрим еще несколько примеров сложения в двоичной системе счисления:
/ 1111 11111 1 111,1
100 1 110 1 11111 10 100 11,111
+ 10 Ю + 10 1 1 + _____ 1 + 1 100 1,1 10
10011 11000 100000 1101101,101
Вычитание.При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее число и ставится соответствующий знак. В таблице вычитания точка означает заем в старшем разряде, который переходит в младший разряд как д единиц.
Примеры.
Вычитание в десятичной системе счисления: 201,2510 -59,7510.
Вычитание в двоичной системе счисления: 11001001,01, — 111011,112.
1 100 100 1,0 1 00111011,11 1000 110 1,10
Рассмотрим еще несколько примеров вычитания в десятичной системе счисления:
110 110 10 1 10 11100 1,1
Ю10 111111000 110 1,1
00 10 10 110 00 10 1 100,0
Умножение.Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при» этом Результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение в двоичной системе счисления
Примеры.
Рассмотрим несколько примеров умножения в двоичной системе счисления:
| 100 1, 1 | 1 1 0 0,0 1 | 1 0 0 0 0 0, 1 |
| * 10,1 | х 10,0 1 | |
| 100 11 | 110001 | |
| + 1 0 0 11 | + 11000 1 | + 1 0 0 0 0 0 1 |
| 101 1 1, 1 1 | 1 0 0 1 0 0, 1 1 | 100 1001,00 1 |
Деление.Деление в любой позиционной системе счисления производится по тем же правилам, что и деление углом в десяnbой системе счисления. В двоичной системе счисления деление выполняется особенно просто: ведь очередная цифра частного может быть только нулем или единицей.
Примеры.Разделить 5865 на 115.
Деление в десятичной системе счисления: 586510 : 115ш.
| 5865 115 |
| 5 1 |
| 1 15 1 15 |
Деление (5865 : 115) 10 в двоичной системе счисления: 10И01И010012:11100112.
Представление информации в компьютере
Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся остальная информация (например, звук, видео, графические изображения и т.д.) перед обработкой на компьютере должна быть преобразована в числовую форму. Так, чтобы привести к цифровому виду (оцифровать) музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в числовой форме. Затем, с помощью специальной компьютерной программы осуществляются необходимые преобразования полученных данных: наложение звуков от различных источников друг на друга (эффект оркестра), изменение тональности отдельных звуков и т.п. После чего, окончательный результат преобразуется обратно в звуковую форму.
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Двоичная система счисления. В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т.д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
Десятичная система счисления. Пришла в Европу из Индии, где она появилась не позднее VI века н.э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т.д.
Восьмеричная система счисления. В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления. Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем — 16 (десятичное), в следующем — 256 (десятичное) и т.д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
Существуют позиционные и непозиционные системы счисления. В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 * 102 + 5 * 101 + 7 * 100 + 7 * 10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения n-1 qn-1 + an-2 qn-2+ . + a1 q1 + a0 q0 + a-1 q-1 + . + a-m q-m,
где ai — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно .В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д. В любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы счисления.
Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел.
Единицей информации в компьютере является один бит (bit), т.е. двоичный разряд, который может принимать значение 0 или 1. Бит — это фундаментальная единица, определяющая количество информации, подвергаемое обработке или переносимое из одного места в другое. Поскольку биты записываются нулями и единицами, их последовательные совокупности позволяют кодировать двоичные числа (binary numbers) — значение в двоичной системе счисления.
В более привычной для человека десятичной системе счисления (по основанию 10) для представления чисел используется десять символов: 0, 1, 2, 3, 4,5,6,7,8и 9. Чтобы составить число, значение которого в десятичной системе счисления больше 9 (например, 27), комбинируют две цифры: при этом позиции символов имеют определенный смысл. Прогрессия значений, связанная с позицией цифры, возрастает, как показано на рис. 2., пропорционально степени основания.

Рис. 2. Пример представления числа в десятичной системе счисления
Десятичное число, состоящее хотя бы из двух цифр, является суммой различных степеней основания, умноженных на соответствующую цифру. Так, число 10 представляет собой сумму из одного десятка (101) и нуля единиц (100), а число 423 — сумму из четырех сотен (102), двух десятков (101) и трех единиц (100).
Рассмотренный метод представления чисел достаточно универсален и используется в других системах счисления, в которых основание отлично от десяти. Например, в системе с основанием 8 задействовано восемь символов: 0, 1, 2, 3, 4, 5, 6 и 7, а значимость каждой позиции возрастает пропорционально степени числа 8, как показано на рис.3.

Рис. 3. Пример предоставления числа в восьмеричной системе счисления.
Как уже отмечалось, компьютер способен обрабатывать информацию в двоичной системе счисления. В ней используются только два символа 0 и 1, а смещение символа на одну позицию влево увеличивает значение числа пропорционально степени основания 2. На рис. 4 показано восьмибитовое (1 байт) представление числа 58 в двоичной системе счисления.

Рис. 4. Пример представления числа в двоичной системе счисления.