Распределение Лапласа зависит от двух параметров n и p; характеристики распределения выражаются через эти параметры: a = np, . При расчетах вручную используют таблицы дифференциальной и интегральной функции Лапласа . Тогда , где . Эта формула обычно называется как «локальная теорема Лапласа». Интегральная функция Лапласа используется для вычисления вероятности попадания m в заданный интервал: P(m1 £ m £ m2) = Ф(tm2) – Ф(tm1). Эта формула обычно называется как «интегральная теорема Лапласа». При расчетах на компьютере для этих же целей используется функция Excel: НОРМРАСП(m;a;sm;0) – возвращает значения вероятности Pn(m) и НОРМРАСП(m;a;sm;1) – возвращает значения интегральной функции распределения Лапласа F(m) = Ф(tm) + 0,5 (функция F(m) отличается постоянным слагаемым от функции Ф(tm)). Считается, что предельные формулы Лапласа можно применять при n ³ 30, a = np ³ 5 и nq ³ 5. Интегральную формулу Лапласа можно уточнить, если расширить интервал [m1 ; m2] на полшага влево и вправо: P(m1 £ m £ m2) = F(m2 + 1 /2) – F(m1 – 1 /2). Предлагается прямыми расчетами проверить точность локальной, интегральной и скорректированной интегральной формул Лапласа для n = 10, 20, 30, 40, 50 и p = 0,3. Фрагмент рабочего листа Excel приведен ниже.
| A | B | C | D | E | F | G | H | I | J |
| Распределение Лапласа | |||||||||
| Pn(m)=НОРМРАСП(m;a;Sm;0) | a=np | Sm=КОРЕНЬ(npq) | |||||||
| P(m1£m£m2)=НОРМРАСП(m2;a;Sm;1)–НОРМРАСП(m1;a;Sm;1) | Интегральная теорема | ||||||||
| P(m1£m£m2)=НОРМРАСП(m2+1/2;a;Sm;1)–НОРМРАСП(m1-1/2;a;Sm;1) (Скорректированная) | |||||||||
| Бернулли | |||||||||
| n = | Ф(2)-Ф(-1)= | 0,81859 | P([m1;m2]) | n=10 | n=20 | n=30 | n=40 | n=50 | |
| p = | 0,3 | Bernully | 0,8401 | 0,87577 | 0,90647 | 0,87422 | 0,83588 | ||
| q = | 0,7 | M-Sm= | 1,550862 | Laplas | 0,73571 | 0,80996 | 0,86082 | 0,83047 | 0,79069 |
| a = M = | M+2Sm= | 5,898275 | Correct | 0,84183 | 0,87469 | 0,90419 | 0,87395 | 0,83753 | |
| Dm = | 2,1 | m1 = | Error% | -12,43% | -7,51% | -5,04% | -5,00% | -5,41% | |
| Sm = | 1,449138 | m2 = | ErrCorr% | 0,21% | -0,12% | -0,25% | -0,03% | 0,20% | |
| Б е р н у л л и | |||||||||
| m | n=10 | F(m) | Laplas | P(a) | n=10 | n=20 | n=30 | n=40 | n=50 |
| 0,028248 | 0,028248 | 0,032298 | Bernully | 0,26683 | 0,19164 | 0,15729 | 0,13657 | 0,12235 | |
| 0,121061 | 0,149308 | 0,106215 | Laplas | 0,27530 | 0,19466 | 0,15894 | 0,13765 | 0,12312 | |
| 0,233474 | 0,382783 | 0,216969 | Correct | 0,26993 | 0,19275 | 0,15790 | 0,13697 | 0,12263 | |
| 0,266828 | 0,649611 | 0,275296 | Error% | 3,17% | 1,58% | 1,05% | 0,79% | 0,63% | |
| 0,200121 | 0,849732 | 0,216969 | ErrCorr% | 1,16% | 0,58% | 0,39% | 0,29% | 0,23% | |
| 0,102919 | 0,952651 | 0,106215 | |||||||
| 0,036757 | 0,989408 | 0,032298 | |||||||
| 0,009002 | 0,998410 | 0,006100 | |||||||
| 0,001447 | 0,999856 | 0,000716 | |||||||
| 0,000138 | 0,999994 | 5,22E-05 | |||||||
| 5,909E-06 | 1,000000 | 2,36E-06 |
Слева в столбцах А, В расположен блок расчетов по формуле Бернулли (сейчас принято n = 10). В соседнем столбце С приведены значения кумуляты (накопленных вероятностей) F(m) = S Pn(k), вычисленных по реккурентной формуле F(m) = F(m–1) + Pn(m), где F(0) = Pn(0) = q n . С помощью кумуляты одним вычитанием определяются вероятности попадания случайной величины m в любые заданные интервалы P(m1 £ m £ m2) = F(m2) – F(m1–1). Так, вероятность P(2£ m £6) можно вычислить как разность F(6) – F(1) = 0,989408 – 0,149308 = 0,840140; это же значение можно получить непосредственно, складывая вероятности Pn(m) для m =2, 3, 4, 5, 6 (цифры на сером фоне в столбце В). В следующем столбце D вычислены вероятности по локальной формуле Лапласа. По результатам расчетов построены графики распределения Бернулли и распределения Лапласа с теми же характеристиками. Изменяя n в ячейке В6, можно наблюдать, насколько хорошо распределение Бернулли описывается предельным распределением Лапласа. Ниже приведены два сравнительных графика для n = 10 и n = 20, откуда видно, что уже при n ³ 20 распределение Бернулли для р = 0,3 практически совпадает с предельным распределением. Таким образом, мы убедились, что локальная формула Лапласа достаточно точная.
Переходим к проверке точности расчетов по интегральной формуле Лапласа. Рассмотрим вероятность попадания случайной величины m в интервал [M – Sm; M + 2Sm]. Теоретически указанная вероятность вычисляется как разность Ф(2) – Ф(-1) = 0,81859. Однако формула эта выведена для непрерывного распределения, а распределение Лапласа – дискретное. Поэтому теоретическое значение (или близкое к нему) может быть получено только для очень большого n > 200. Проверим это утверждение. Выше над блоком расчетов по формуле Бернулли в столбцах C, D вычислены границы интервала: M – Sm = 1,551 и M + 2Sm = 5,898; полученные границы округлены до ближайших целых m1 = 2, m2 = 6. Необходимо сравнить точное значение P(2£ m £6) = 0,8401, полученное ранее с помощью кумуляты распределения Бернулли, с соответствующим значением по интегральной формуле Лапласа P(2£ m £6) » НОРМРАСП(6;a;Sm;1)–НОРМРАСП(2;a;Sm;1) = 0,73571. По сравнению с точным значением (0,8401) ошибка составила -12,43%. Эти расчеты оформлены в виде таблицы в строках 6–11 столбцы E, F. При изменении n в ячейке B6 все цифры в столбце F автоматически корректируются. Для того, чтобы сохранить результаты предыдущих расчетов, они были cкопированы Специальной вставкой – Только значения в продолжение таблицы вправо (столбцы G, H, I, J). Рассматривая заполненную таблицу (диапазон E6:J11), убеждаемся в довольно медленном приближении предельной формулы к точному значению. Теперь мы можем оценить эффективность скорректированной интегральной формулы Лапласа P(2 £ m £ 6) = НОРМРАСП(6,5;a;Sm;1)–НОРМРАСП(1,5;a;Sm;1) , которая уже для n = 10 привела к практически точному значению 0,8418 (погрешность 0,21%). Эффективность скорректированной формулы была также проверена на вычислении вероятности моды (наивероятнейшего значения m = a = np). Эти расчеты выполнены в таблице диапазона E13:J18. Интегральная функция Лапласа здесь дает значение 0, поэтому в таблице использовалась локальная формула Лапласа. Погрешности локальной формулы небольшие и быстро убывают с увеличением n (при n = 20 погрешность составляет всего 1,6%). Скорректированная интегральная формула оказалась еще более точной; она дает практически точные значения уже при n = 10.
Вычисление функции Лапласа в Microsoft Excel

Одной из самых известных неэлементарных функций, которая применяется в математике, в теории дифференциальных уравнений, в статистике и в теории вероятностей является функция Лапласа. Решение задач с ней требует существенной подготовки. Давайте выясним, как можно с помощью инструментов Excel произвести вычисление данного показателя.
Функция Лапласа
Функция Лапласа имеет широкое прикладное и теоретическое применение. Например, она довольно часто используется для решения дифференциальных уравнений. У этого термина существует ещё одно равнозначное название – интеграл вероятности. В некоторых случаях основой для решения является построение таблицы значений.
Оператор НОРМ.СТ.РАСП
В Экселе указанная задача решается с помощью оператора НОРМ.СТ.РАСП. Его название является сокращением от термина «нормальное стандартное распределение». Так как его главной задачей является возврат в выделенную ячейку стандартного нормального интегрального распределения. Данный оператор относится к статистической категории стандартных функций Excel.
В Excel 2007 и в более ранних версиях программы этот оператор назывался НОРМСТРАСП. Он в целях совместимости оставлен и в современных версиях приложений. Но все-таки в них рекомендуется использование более продвинутого аналога – НОРМ.СТ.РАСП.
Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:
Устаревший оператор НОРМСТРАСП записывается так:
Как видим, в новом варианте к существующему аргументу «Z» добавлен аргумент «Интегральная». Нужно заметить, что каждый аргумент является обязательным.
Аргумент «Z» указывает числовое значение, для которого производится построение распределения.
Аргумент «Интегральная» представляет собой логическое значение, которое может иметь представление «ИСТИНА» («1») или «ЛОЖЬ» («0»). В первом случае в указанную ячейку возвращается интегральная функция распределения, а во втором – весовая функция распределения.
Решение задачи
Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:
Теперь давайте на конкретном примере рассмотрим использование оператора НОРМ.СТ.РАСП для решения конкретной задачи.
-
Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.
После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».

Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».
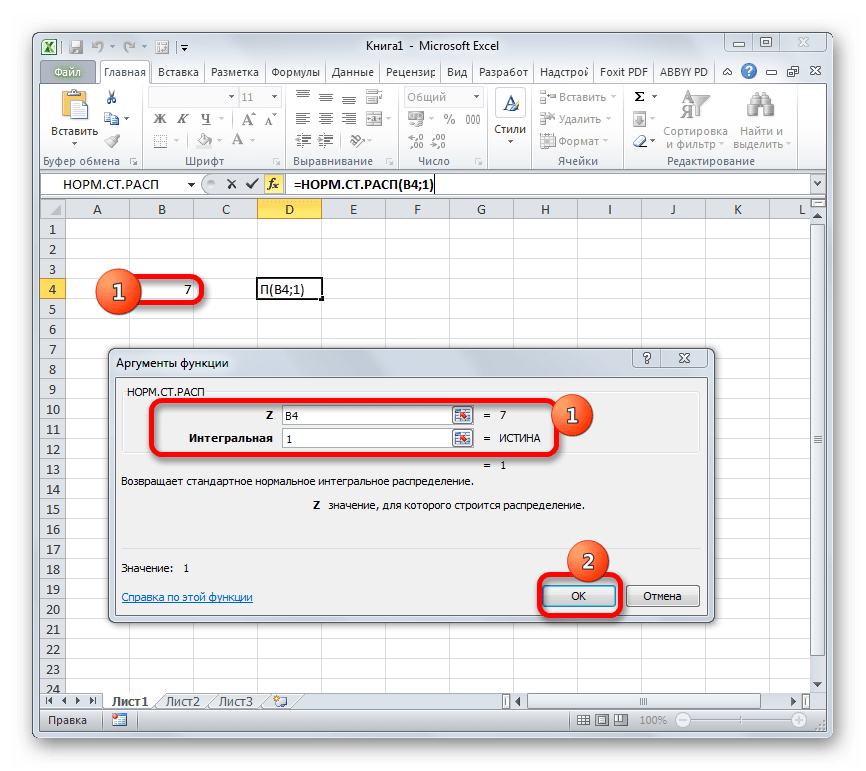
После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.
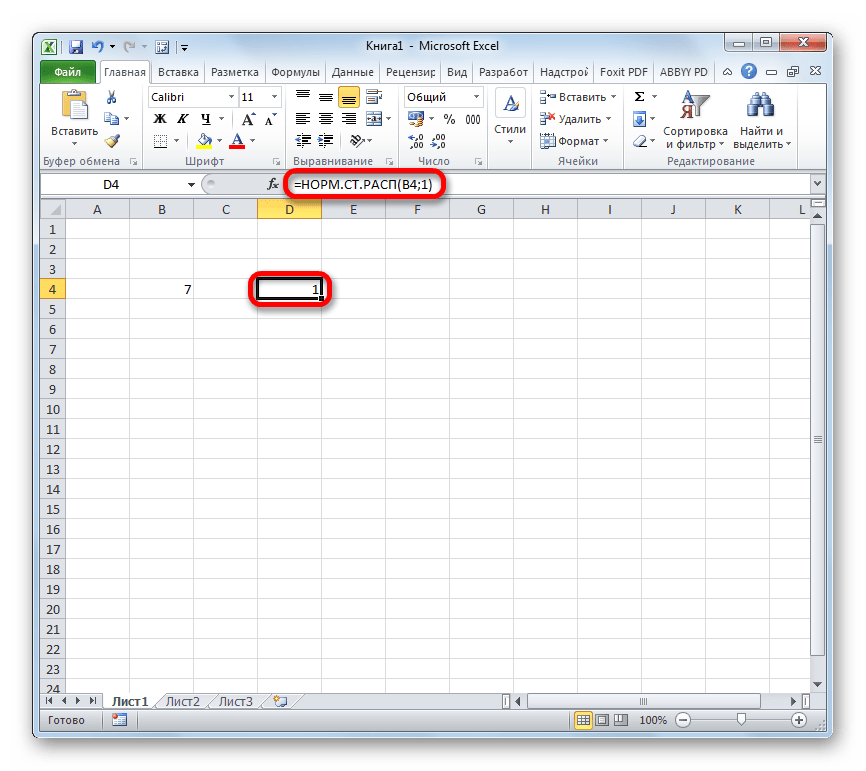
Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.


Как видим, вычислить функцию Лапласа для конкретного заданного числового значения в программе Excel не составляет особенного труда. Для этих целей применяется стандартный оператор НОРМ.СТ.РАСП.
 Мы рады, что смогли помочь Вам в решении проблемы.
Мы рады, что смогли помочь Вам в решении проблемы.
Добавьте сайт Lumpics.ru в закладки и мы еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
 Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Обчислення функції Лапласа в Microsoft Excel

Однією з найвідоміших неелементарних функцій, яка застосовується в математиці, в теорії диференціальних рівнянь, в статистиці і в теорії ймовірностей є функція Лапласа. Рішення задач з нею потребує суттєвого підготовки. Давайте з’ясуємо, як можна за допомогою інструментів Excel зробити обчислення даного показника.
функція Лапласа
Функція Лапласа має широке прикладне і теоретичне застосування. Наприклад, вона досить часто використовується для вирішення диференціальних рівнянь. Цей термін існує ще одне рівнозначне назва — інтеграл ймовірності. У деяких випадках основою для вирішення є побудова таблиці значень.
оператор НОРМ.СТ.РАСП
У Ексель зазначена завдання вирішується за допомогою оператора НОРМ.СТ.РАСП. Його назва є скороченням від терміна «нормальне стандартний розподіл». Так як його головним завданням є повернення в виділену клітинку стандартного нормального інтегрального розподілу. Даний оператор відноситься до статистичної категорії стандартних функцій Excel.
В Excel 2007 і в більш ранніх версіях програми цей оператор називався НОРМСТРАСП. Він з метою сумісності залишений і в сучасних версіях додатків. Але все-таки в них рекомендується використання більш просунутого аналога — НОРМ.СТ.РАСП.
Синтаксис оператора НОРМ.СТ.РАСП виглядає наступним чином:
Застарілий оператор НОРМСТРАСП записується так:
Як бачимо, в новому варіанті до існуючого аргументу «Z» доданий аргумент «Інтегральна». Потрібно зауважити, що кожен аргумент є обов’язковим.
Аргумент «Z» вказує числове значення, для якого проводиться побудова розподілу.
Аргумент «Інтегральна» являє собою логічне значення, яке може мати уявлення «ІСТИНА» ( «1») або «БРЕХНЯ» ( «0»). У першому випадку в зазначену осередок повертається інтегральна функція розподілу, а в другому — вагова функція розподілу.
Рішення завдання
Для того щоб виконати необхідну обчислення для змінної застосовується наступна формула:
Тепер давайте на конкретному прикладі розглянемо використання оператора НОРМ.СТ.РАСП для вирішення конкретного завдання.
- Виділяємо осередок, куди буде виводитися готовий результат і клацаємо по значку «Вставити функцію», розташованому біля рядка формул.
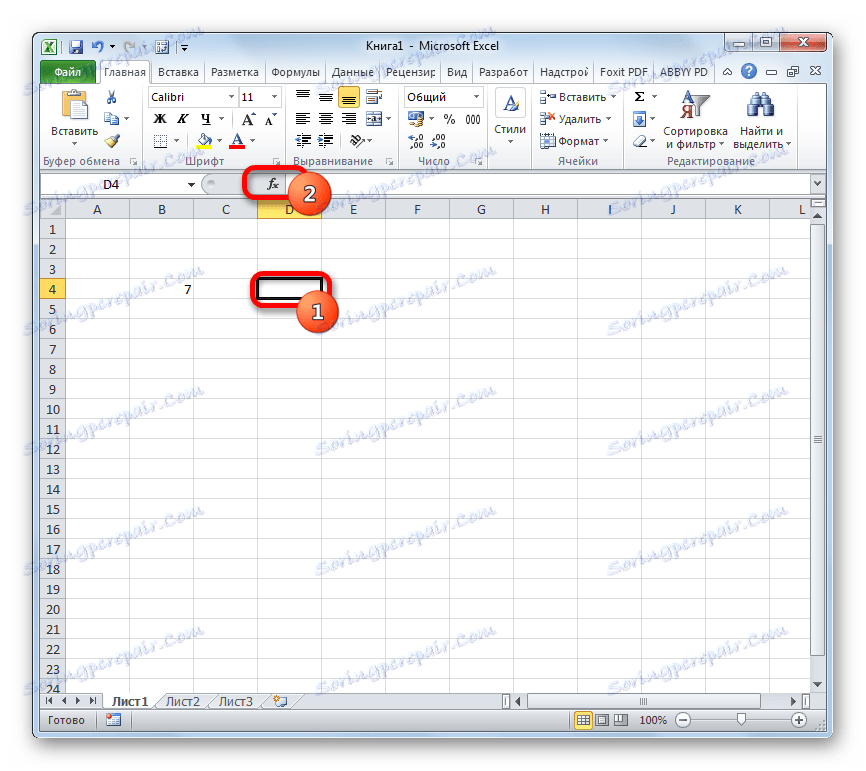
Після відкриття Майстра функцій переходимо в категорію «Статистичні» або «Повний алфавітний перелік». Виділяємо найменування «НОРМ.СТ.РАСП» і тиснемо на кнопку «OK».
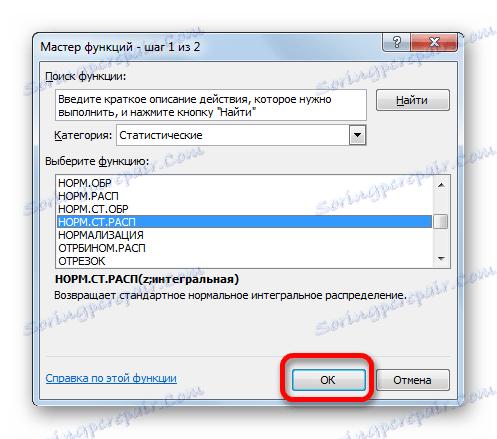
Відбувається активація вікна аргументів оператора НОРМ.СТ.РАСП. В поле «Z» вводимо змінну, до якої потрібно провести розрахунок. Також цей аргумент може бути представлений у вигляді посилання на осередок, яка містить цю змінну. В поле «Інтегральна» вводимо значення «1». Це означає, що оператор після обчислення поверне в якості рішення інтегральну функцію розподілу. Після того, як виконані перераховані вище дії, тиснемо на кнопку «OK».
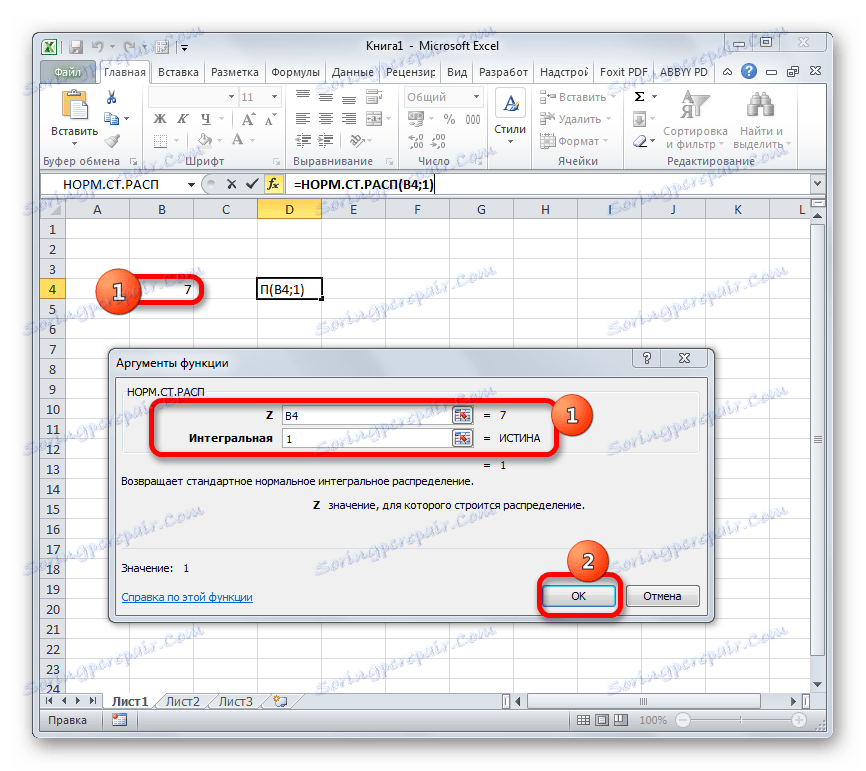
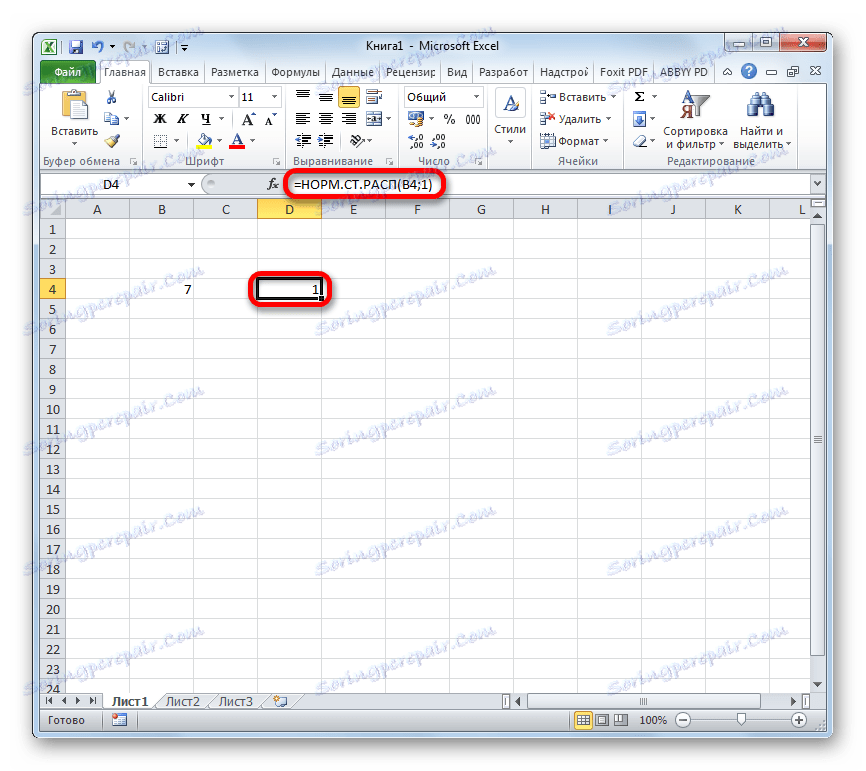
Після цього результат обробки даних оператором НОРМ.СТ.РАСП буде виведений в клітинку, яка вказана в першому пункті даного керівництва.
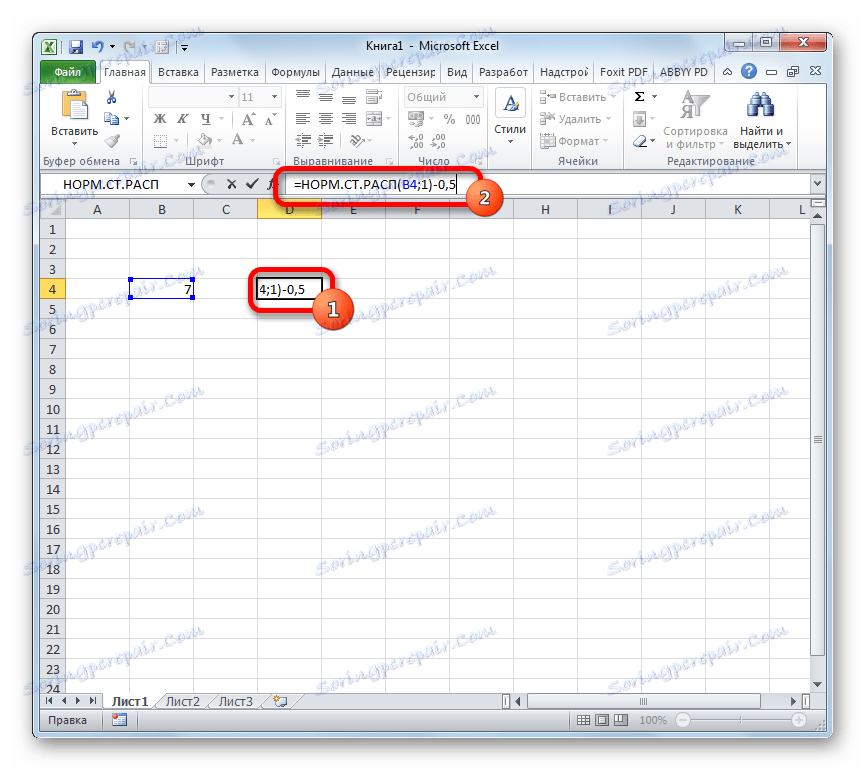
Але і це ще не все. Ми вирахували тільки стандартний нормальний інтегральний розподіл. Для того, щоб порахувати значення функції Лапласа, потрібно від нього забрати число 0,5. Виділяємо осередок, що містить вираз. У рядку формул після оператора НОРМ.СТ.РАСП дописуємо значення: -0,5.
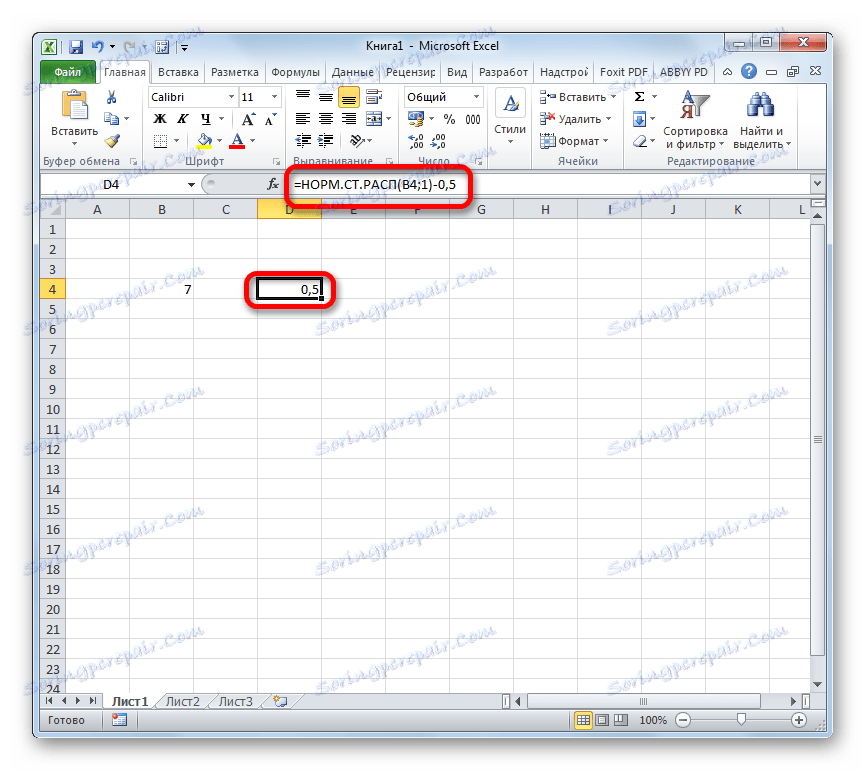
Як бачимо, обчислити функцію Лапласа для конкретного заданого числового значення в програмі Excel не складає особливих труднощів. Для цих цілей застосовується стандартний оператор НОРМ.СТ.РАСП.
Функция Лапласа и другие табличные статистические функции: в Excel формуле
Привет, сегодня поговорим про функция лапласа, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое функция лапласа,другие табличные статистические в excel формуле , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ
функция лапласа и другие табличные статистические функции: считаем в Excel
При решении таких типовых задач математической статистики, как построение доверительных интервалов или проверка гипотез о параметрах случайных величин, широко используются несколько табличных функций, например, функция Лапласа или квантили распределения хи- квадрат .
В наше время совершенно необязательно обращаться за недостающими в формуле величинами к толстым справочникам со статистическими таблицами, можно все посчитать непосредственно в Excel:
Формула =НОРМСТРАСП(x)-0,5 вычисляет значение функции Лапласа от аргумента x (подставьте вместо x соответствующую ячейку) . Об этом говорит сайт https://intellect.icu . При этом Ф(-x)=-Ф(x) , а при x>3,85 значение Ф(x)=0,5 .
Вычислить значение обратной функции Лапласа от аргумента x можно формулой =НОРМСТОБР(x) . В Excel функция НОРМСТОБР (1-eps/2) даст требуемое критическое значение, соответствующее уровню значимости критерия, равному eps. Например, для критерия с критическим уровнем 0,05 (5%) формула НОРМСТОБР(1-0,05/2)=1,96
Критические точки t-критерия можно вычислить с помощью формулы =СТЬЮДРАСПОБР(α,n) , где α – уровень значимости ( вероятность γ или надежность 1-γ ), n – число степеней свободы (например, объем выборки в задачах о построении доверительных интервалов). При числе степеней свободы n≥30 распределение сводится к нормальному с параметрами α=0 , σ= корень (n/(n-2)) .
Критические точки распределения Пирсона χ 2 можно вычислить с помощью формулы =ХИ2ОБР(a,n) , где a – уровень значимости, n – число степеней свободы.
Получить значение функции плотности распределения Пуассона можно с помощью формулы =ПУАССОН(n,λ,0) , где n – число степеней свободы (количество событий), λ – среднее число появлений события (ожидаемое численное значение).
В ряде случаев для расчета с заданным значением параметра γ функции Excel может понадобиться передать аргумент функции α=1-γ , смотрите внимательно встроенную справку по функциям.
Распределение Стьюдента
Понравилась статья про функция лапласа? Откомментируйте её Надеюсь, что теперь ты понял что такое функция лапласа,другие табличные статистические в excel формуле и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Функция лапласа в excel
БлогNot. Функция Лапласа и другие табличные статистические функции: считаем в Excel
Функция Лапласа и другие табличные статистические функции: считаем в Excel
При решении таких типовых задач математической статистики, как построение доверительных интервалов или проверка гипотез о параметрах случайных величин, широко используются несколько табличных функций, например, функция Лапласа или квантили распределения хи-квадрат.
В наше время совершенно необязательно обращаться за недостающими в формуле величинами к толстым справочникам со статистическими таблицами, можно всё посчитать непосредственно в Excel:
Формула =НОРМСТРАСП(x)-0,5 вычисляет значение функции Лапласа от аргумента x (подставьте вместо x соответствующую ячейку). При этом Ф(-x)=-Ф(x) , а при x>3,85 значение Ф(x)=0,5 .
Вычислить значение обратной функции Лапласа от аргумента x можно формулой =НОРМСТОБР(x) . В Excel функция НОРМСТОБР (1-eps/2) даст требуемое критическое значение, соответствующее уровню значимости критерия, равному eps. Например, для критерия с критическим уровнем 0,05 (5%) формула НОРМСТОБР(1-0,05/2)=1,96
Критические точки t-критерия можно вычислить с помощью формулы =СТЬЮДРАСПОБР(α;n) , где α – уровень значимости (вероятность γ или надёжность 1-γ ), n – число степеней свободы (например, объём выборки в задачах о построении доверительных интервалов). При числе степеней свободы n≥30 распределение сводится к нормальному с параметрами α=0 , σ=корень(n/(n-2)) .
Критические точки распределения Пирсона χ 2 можно вычислить с помощью формулы =ХИ2ОБР(a;n) , где a – уровень значимости, n – число степеней свободы.
Получить значение функции плотности распределения Пуассона можно с помощью формулы =ПУАССОН(n;λ;0) , где n – число степеней свободы (количество событий), λ – среднее число появлений события (ожидаемое численное значение).
В ряде случаев для расчёта с заданным значением параметра γ функции Excel может понадобиться передать аргумент функции α=1-γ , смотрите внимательно встроенную справку по функциям.
Математическая статистика — лекции и примеры в Excel
12.03.2013, 17:18; рейтинг: 43632

Одной из самых известных неэлементарных функций, которая применяется в математике, в теории дифференциальных уравнений, в статистике и в теории вероятностей является функция Лапласа. Решение задач с ней требует существенной подготовки. Давайте выясним, как можно с помощью инструментов Excel произвести вычисление данного показателя.
Функция Лапласа
Функция Лапласа имеет широкое прикладное и теоретическое применение. Например, она довольно часто используется для решения дифференциальных уравнений. У этого термина существует ещё одно равнозначное название – интеграл вероятности. В некоторых случаях основой для решения является построение таблицы значений.
Оператор НОРМ.СТ.РАСП
В Экселе указанная задача решается с помощью оператора НОРМ.СТ.РАСП. Его название является сокращением от термина «нормальное стандартное распределение». Так как его главной задачей является возврат в выделенную ячейку стандартного нормального интегрального распределения. Данный оператор относится к статистической категории стандартных функций Excel.
В Excel 2007 и в более ранних версиях программы этот оператор назывался НОРМСТРАСП. Он в целях совместимости оставлен и в современных версиях приложений. Но все-таки в них рекомендуется использование более продвинутого аналога – НОРМ.СТ.РАСП.
Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:
Устаревший оператор НОРМСТРАСП записывается так:
Как видим, в новом варианте к существующему аргументу «Z» добавлен аргумент «Интегральная». Нужно заметить, что каждый аргумент является обязательным.
Аргумент «Z» указывает числовое значение, для которого производится построение распределения.
Аргумент «Интегральная» представляет собой логическое значение, которое может иметь представление «ИСТИНА» («1») или «ЛОЖЬ» («0»). В первом случае в указанную ячейку возвращается интегральная функция распределения, а во втором – весовая функция распределения.
Решение задачи
Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:
Теперь давайте на конкретном примере рассмотрим использование оператора НОРМ.СТ.РАСП для решения конкретной задачи.
-
Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.

После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».

Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».

После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.

Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.

Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.

Как видим, вычислить функцию Лапласа для конкретного заданного числового значения в программе Excel не составляет особенного труда. Для этих целей применяется стандартный оператор НОРМ.СТ.РАСП.

Однією з найвідоміших неелементарних функцій, яка застосовується в математиці, в теорії диференціальних рівнянь, в статистиці і в теорії ймовірностей є функція Лапласа. Рішення задач з нею потребує суттєвого підготовки. Давайте з’ясуємо, як можна за допомогою інструментів Excel зробити обчислення даного показника.
функція Лапласа
Функція Лапласа має широке прикладне і теоретичне застосування. Наприклад, вона досить часто використовується для вирішення диференціальних рівнянь. Цей термін існує ще одне рівнозначне назва — інтеграл ймовірності. У деяких випадках основою для вирішення є побудова таблиці значень.
оператор НОРМ.СТ.РАСП
У Ексель зазначена завдання вирішується за допомогою оператора НОРМ.СТ.РАСП. Його назва є скороченням від терміна «нормальне стандартний розподіл». Так як його головним завданням є повернення в виділену клітинку стандартного нормального інтегрального розподілу. Даний оператор відноситься до статистичної категорії стандартних функцій Excel.
В Excel 2007 і в більш ранніх версіях програми цей оператор називався НОРМСТРАСП. Він з метою сумісності залишений і в сучасних версіях додатків. Але все-таки в них рекомендується використання більш просунутого аналога — НОРМ.СТ.РАСП.
Синтаксис оператора НОРМ.СТ.РАСП виглядає наступним чином:
Застарілий оператор НОРМСТРАСП записується так:
Як бачимо, в новому варіанті до існуючого аргументу «Z» доданий аргумент «Інтегральна». Потрібно зауважити, що кожен аргумент є обов’язковим.
Аргумент «Z» вказує числове значення, для якого проводиться побудова розподілу.
Аргумент «Інтегральна» являє собою логічне значення, яке може мати уявлення «ІСТИНА» ( «1») або «БРЕХНЯ» ( «0»). У першому випадку в зазначену осередок повертається інтегральна функція розподілу, а в другому — вагова функція розподілу.
Рішення завдання
Для того щоб виконати необхідну обчислення для змінної застосовується наступна формула:
Тепер давайте на конкретному прикладі розглянемо використання оператора НОРМ.СТ.РАСП для вирішення конкретного завдання.
- Виділяємо осередок, куди буде виводитися готовий результат і клацаємо по значку «Вставити функцію», розташованому біля рядка формул.

Після відкриття Майстра функцій переходимо в категорію «Статистичні» або «Повний алфавітний перелік». Виділяємо найменування «НОРМ.СТ.РАСП» і тиснемо на кнопку «OK».

Відбувається активація вікна аргументів оператора НОРМ.СТ.РАСП. В поле «Z» вводимо змінну, до якої потрібно провести розрахунок. Також цей аргумент може бути представлений у вигляді посилання на осередок, яка містить цю змінну. В поле «Інтегральна» вводимо значення «1». Це означає, що оператор після обчислення поверне в якості рішення інтегральну функцію розподілу. Після того, як виконані перераховані вище дії, тиснемо на кнопку «OK».

Після цього результат обробки даних оператором НОРМ.СТ.РАСП буде виведений в клітинку, яка вказана в першому пункті даного керівництва.

Але і це ще не все. Ми вирахували тільки стандартний нормальний інтегральний розподіл. Для того, щоб порахувати значення функції Лапласа, потрібно від нього забрати число 0,5. Виділяємо осередок, що містить вираз. У рядку формул після оператора НОРМ.СТ.РАСП дописуємо значення: -0,5.

Для того, щоб зробити обчислення, тиснемо на кнопку Enter. Отриманий результат і буде шуканим значенням.

Як бачимо, обчислити функцію Лапласа для конкретного заданого числового значення в програмі Excel не складає особливих труднощів. Для цих цілей застосовується стандартний оператор НОРМ.СТ.РАСП.