Что такое арифметико-логическое устройство (АЛУ)

Арифметико-логическое устройство

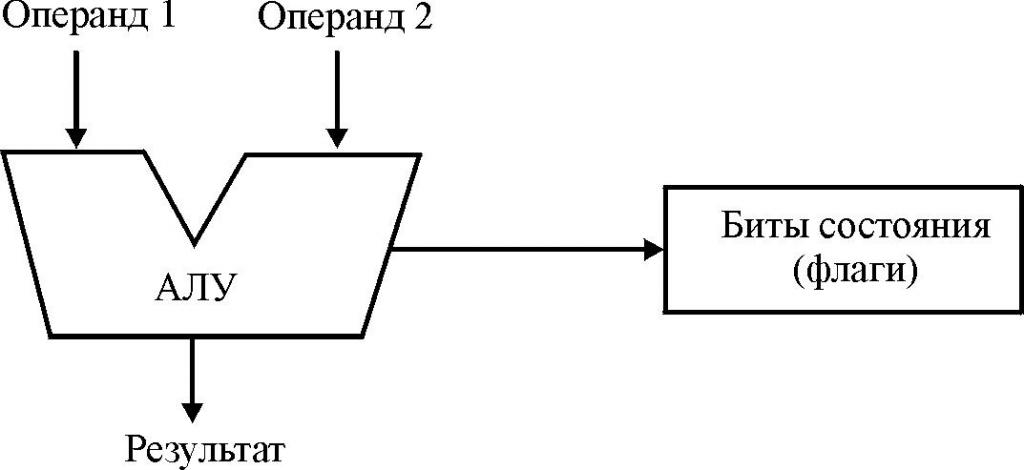
Арифметико-логическое устройство (АЛУ) — центральная часть процессора, выполняющая арифметические и логические операции.

АЛУ реализует важную часть процесса обработки данных. Она заключается в выполнении набора простых операций. Операции АЛУ подразделяются на три основные категории: арифметические, логические и операции над битами. Арифметической операцией называют процедуру обработки данных, аргументы и результат которой являются числами (сложение, вычитание, умножение, деление. ). Логической операцией именуют процедуру, осуществляющую построение сложного высказывания (операции И, ИЛИ, НЕ. ). Операции над битами обычно подразумевают сдвиги.

Определение понятия

Арифметико-логическое устройство — один из блоков процессора, управляемый УУ (устройством управления). Его предназначение: выполнение логических и арифметических преобразований над данными-операндами (аргументами операции, информацией, обрабатываемой программой). Разрядность операндов в данном случае — размер или длина машинного слова.

Современное многофункциональное АЛУ состоит сегодня из двух частей:

• Операционное устройство.
• Устройство управления. Проводит вторичную дешифрацию кодов команды, определяет операцию, выполняемую в арифметико-логическом устройстве.

Сумматоры

Четвертьсумматор

Четвертьсумматором называют элемент «Исключающее Или». Почему? Давайте разберемся.
Составим таблицу сложения для двух чисел в двоичной системе счисления:
0+0= 0
0+1= 1
1+0= 1
1+1= 10

Теперь запишем таблицу истинности элемента «Исключающее Или». Для этого обозначим светящуюся лампочку за 1, потухшую — за 0, и ответы друга «Да»/«Нет» как 1 и 0 соответственно.
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0

Очень похоже, не так ли? Таблица сложения и таблица истинности «Исключающего Или» совпадают полностью, кроме одного-единственного случая. И этот случай называется «Переполнение».

Полусумматор

При переполнении результат сложения уже не помещается в столько же разрядов, во сколько помещались слагаемые. Слагаемые — два однозначных числа (одна значащая цифра, понимаете?), а сумма — уже двузначное (две значащих цифры). Две цифры одной лампочкой («Светится»/«Не светится») уже не передать. Нужно две лампочки. Нужно — сделаем!

Кроме XOR, для сумматора нам потребуется элемент «И» (AND).
0 XOR 0 = 0 0 AND 0 = 0
0 XOR 1 = 1 0 AND 1 = 0
1 XOR 0 = 1 1 AND 0 = 0
1 XOR 1 = 0 1 AND 1 = 1

Тадам!
0+0= 00
0+1= 01
1+0= 01
1+1= 10

Наша вундервафля полусумматор работает. Его можно считать простейшим специализированным процессором, который складывает два числа. Полусумматор называется полусумматором потому, что с его помощью нельзя учитывать перенос (результат работы другого сумматора), то есть нельзя складывать три однозначных двоичных числа. В связи с этим из нескольких одноразрядных полусумматоров нельзя сделать один многоразрядный.

Я не буду вдаваться в подробности работы полных и многоразрядных сумматоров, просто надеюсь, что основную идею вы уловили.

Операция переполнения в АЛУ

После выполнения каждой операции в сумматоре–вычита­теле формируется флаг переполнения MV, который заносится в позицию ASTAT.6 регистра арифметического статуса ASTAT (табл. 8.3.7). Флаг переполне­ния устанавливается (MV = 1) в том случае, если результат на выходе сумматора–вычитателя, интерпретируемый как число с дополнением до 2, пересекает 32–бит­ную границу. В этом случае 9 старших (знаковых) разрядов 40–битного регистра результата не равны одновременно 0 или 1.

Эта операция выполняется при установленном флаге переполне­ния (MV = 1) в регистре арифметического статуса ASTAT (табл. 8.3.7). В ре­зультате операции содержимое регистра результата MR принимает максимальное:

• положительное значение 00000000 0111111111111111 1111111111111111, если старший разряд регистра MR1 равен 0;
• отрицательное значение 11111111 1000000000000000 0000000000000000, если старший разряд регистра MR1 равен 1. Операция насыщения используется после умножений–аккумуляций для конт­роля правильности полученных результатов. Если MV = 0, то операция насыщения оставляет результат неизменным.

Инструкции микропроцессора

Даже простейший микропроцессор способен обрабатывать достаточно большой набор инструкций. Набор инструкций является своего рода шаблоном. Каждая из этих загружаемых в регистр команд инструкций имеет свое значение. Людям непросто запомнить последовательность битов, поэтому каждая инструкция описывается в виде короткого слова, каждое из которых отражает определенную команду. Эти слова составляют язык ассемблера процессора. Ассемблер переводит эти слова на понятный процессору язык двоичных кодов.

Приведем список слов-команд языка ассемблера для условного простого процессора, который мы рассматриваем в качестве примера к нашему повествованию:

• LOADA mem — Загрузить (load) регистр A из некоторого адреса памяти
• LOADB mem — Загрузить (load) регистр B из некоторого адреса памяти
• CONB con — Загрузить постоянное значение (constant value) в регистр B
• SAVEB mem — Сохранить (save) значение регистра B в памяти по определенному адресу
• SAVEC mem — Сохранить (save) значение регистра C в памяти по определенному адресу
• ADD — Сложить (add) значения регистров A и B. Результат действия сохранить в регистре C
• SUB — Вычесть (subtract) значение регистра B из значения регистра A. Результат действия сохранить в регистре C
• MUL — Перемножить (multiply) значения регистров A и B. Результат действия сохранить в регистре C
• DIV — Разделить (divide) значение регистра A на значение регистра B. Результат действия сохранить в регистре C
• COM — Сравнить (compare) значения регистров A и B. Результат передать в тестовый регистр
• JUMP addr — Перепрыгнуть (jump) к указанному адресу
• JEQ addr — Если выполняется условие равенства значений двух регистров, перепрыгнуть (jump) к указанному адресу
• JNEQ addr — Если условие равенства значений двух регистров не выполняется, перепрыгнуть (jump) к указанному адресу
• JG addr — Если значение больше, перепрыгнуть (jump) к указанному адресу
• JGE addr — Если значение больше или равно, перепрыгнуть (jump) к указанному адресу
• JL addr — Если значение меньше, перепрыгнуть (jump) к указанному адресу
• JLE addr — Если значение меньше или равно, перепрыгнуть (jump) к указанному адресу
• STOP — Остановить (stop) выполнение

Английские слова, обозначающие выполняемые действия, в скобках приведены неспроста. Так мы можем видеть, что язык ассемблера (как и многие другие языки программирования) основан на английском языке, то есть на привычном средстве общения тех людей, которые создавали цифровые технологии.

Содержание

Разработчик компьютера ENIAC, Джон фон Нейман, был первым создателем АЛУ. В 1945 году он опубликовал первые научные работы по новому компьютеру, названному EDVAC (Electronic Discrete Variable Computer). Годом позже он работал со своими коллегами над разработкой компьютера для Принстонского института новейших исследований (IAS). Архитектура этого компьютера позже стала прототипом архитектур большинства последующих компьютеров. В своих работах фон Нейман указывал устройства, которые, как он считал, должны присутствовать в компьютерах. Среди этих устройств присутствовало и АЛУ. Фон Нейман отмечал, что АЛУ необходимо для компьютера, поскольку оно гарантирует, что компьютер будет способен выполнять базовые математические операции включая сложение, вычитание, умножение и деление

АЛУ состоит из регистров, сумматора с соответствующими логическими схемами и элемента управления выполняемым процессом. Устройство работает в соответствии с сообщаемыми ему именами (кодами) операций, которые при пересылке данных нужно выполнить над переменными, помещаемыми в регистры.

Арифметико-логическое устройство функционально можно разделить на две части :

1. микропрограммное устройство (устройство управления), задающее последовательность микрокоманд (команд);
2. операционное устройство (АЛУ), в котором реализуется заданная последовательность микрокоманд (команд).

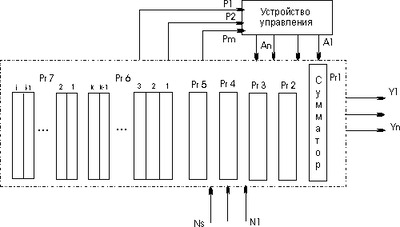
Рисунок 1 — Структурная схема арифметико-логического устройства

Структурная схема АЛУ и его связь с другими блоками машины показаны на рисунке 1. В состав АЛУ входят регистры Рг1 — Рг7, в которых обрабатывается информация , поступающая из оперативной или пассивной памяти N1, N2, . NS; логические схемы, реализующие обработку слов по микрокомандам, поступающим из устройства управления.

Закон переработки информации задает микропрограмма , которая записывается в виде последовательности микрокоманд A1,A2, . Аn-1,An. При этом различают два вида микрокоманд: внешние, то есть такие микрокоманды, которые поступают в АЛУ от внешних источников и вызывают в нем те или иные преобразования информации (на рис. 1 микрокоманды A1,A2. Аn), и внутренние, которые генерируются в АЛУ и воздействуют на микропрограммное устройство, изменяя естественный порядок следования микрокоманд. Например, АЛУ может генерировать признаки в зависимости от результата вычислений: признак переполнения, признак отрицательного числа, признак равенства 0 всех разрядов числа др. На рис. 1 эти микрокоманды обозначены р1, p2. рm.

Результаты вычислений из АЛУ передаются по кодовым шинам записи у1, у2, . уs, в ОЗУ. Функции регистров, входящих в АЛУ:

• Рг1 — сумматор (или сумматоры) — основной регистр АЛУ, в котором образуется результат вычислений;
• Рг2, РгЗ — регистры слагаемых, сомножителей, делимого или делителя (в зависимости от выполняемой операции);
• Рг4 — адресный регистр (или адресные регистры), предназначен для запоминания (иногда и формирования) адреса операндов и результата;
• Ргб — k индексных регистров, содержимое которых используется для формирования адресов;
• Рг7 — i вспомогательных регистров, которые по желанию программиста могут быть аккумуляторами, индексными регистрами или использоваться для запоминания промежуточных результатов.

Часть операционных регистров является программно-доступной, то есть они могут быть адресованы в команде для выполнения операций с их содержимым. К ним относятся : сумматор, индексные регистры, некоторые вспомогательные регистры.

Остальные регистры программно-недоступные, так как они не могут быть адресованы в программе. Операционные устройства можно классифицировать по виду обрабатываемой информации, по способу обработки информации и логической структуре.

АЛУ может оперировать четырьмя типами информационных объектов: булевскими (1 бит), цифровыми (4 бита), байтными (8 бит) и адресными (16 бит). В АЛУ выполняется 51 различная операция пересылки или преобразования этих данных. Так как используется 11 режимов адресации (7 для данных и 4 для адресов), то путем комбинирования «операция/ режим адресации» базовое число команд 111 расширяется до 255 из 256 возможных при однобайтном коде операции.

Содержание ChipNews

люди куплю транзистар кт 827А 0688759652

как молоды мы были и как быстро пробежали годы кулотино самое счастливое мое время

Светодиод — это диод который излучает свет. А если диод имеет ИК излучение, то это ИК диод, а не «ИК светодиод» и «Светодиод инфракрасный», как указано на сайте.

Подскажите 2т963а-2 гарантийный срок

Сумматоры: определения, классификация, уравнения, структуры и применение

Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.

Сумматор логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учет знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.

Сумматоры классифицируют по различным признакам.

• двоичные;
• двоично-десятичные (в общем случае двоично-кодированные);
• десятичные;
• прочие (например, амплитудные).

• одноразрядные,
• многоразрядные.

• четвертьсумматоры (элементы «сумма по модулю 2»; элементы «исключающее ИЛИ»), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
• полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноименные разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом перенос в следующий (более старший разряд);
• полные одноразрядные двоичные сумматоры, характеризующиеся наличием трех входов, на которые подаются одноименные разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом перенос в следующий (более старший разряд).

• последовательные, в которых обработка чисел ведется поочередно, разряд за разрядом на одном и том же оборудовании;
• параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется свое оборудование.

Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединенных цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени основная задача при построении параллельных сумматоров.

Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных емкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.

• с последовательным переносом;
• с параллельным переносом;
• с групповой структурой;
• со специальной организацией цепей переноса.

• сумматоры со сквозным переносом, в которых между входом и выходом переноса одноразрядного сумматора оказывается наименьшее число логических уровней [1];
• сумматоры с двухпроводной передачей сигналов переноса [1, 2];
• сумматоры с условным переносом (вариант сумматора с групповой структурой, позволяющий уменьшить время суммирования в 2 раза при увеличении оборудования в 1,5 раза) [3];
• асинхронные сумматоры, вырабатывающие признак завершения операции суммирования, при этом среднее время суммирования уменьшается, поскольку оно существенно меньше максимального.

Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.

• комбинационный, выполняющий микрооперацию «S = A плюс B», в котором результат выдается по мере его образования (это комбинационная схема в общепринятом смысле слова);
• сумматор с сохранением результата «S = A плюс B»;
• накапливающий, выполняющий микрооперацию «S = S плюс B».

Последние две структуры строятся либо на счетных триггерах (сейчас практически не используются), либо по структуре «комбинационный сумматор регистр хранения» (сейчас наиболее употребляемая схема).

• разрядность;
• статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
• динамические параметры. Сумматоры характеризуются четырьмя задержками распространения:
• от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
• от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
• от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
• от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.

2. Логические поразрядные операции

В языке программирования С существуют два вида поразрядных операций: логические операции и операции сдвига [16.1].

Поразрядные операции выполняются над каждым разрядом независимо от разрядов слева или справа. Поразрядные операции выполняются над целыми числами. Рассмотрим логические поразрядные операции.

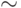
Унарная операция преобразовывает все единицы в нули и все нули в единицы (предполагается, что операции производятся над двоичными числами). Данную операцию называют также операцией «дополнение», т.е. когда все биты, равные 0, устанавливаются в 1, а когда все биты, равные 1, – устанавливаются в 0.

Поразрядная операция И обозначается символом & .

Двоичная операция & создает новое значение за счет выполнения поразрядного сравнения двух операндов. Для каждой позиции результирующий разряд будет иметь значение 1 только в случае, когда соответствующие разряды обоих операндов имеют значение 1. Можно сказать, что когда над двумя значениями производится операция поразрядного умножения & , то двоичные представления чисел сравниваются бит за битом [2]. Например, пусть одна переменная w1 есть число 25, а другая w2 – число 77. Соответственно в двоичном представлении 25 = 0000000000011001, 77 = 0000000001001101. Тогда в результате поразрядной операции & получим число w3 = w1 & w2. Результат действия оператора & можно представить следующим образом:

Поразрядная операция И (&)

w1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 (25)

w2 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 (77)

w3 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 (9)

В результате поразрядной операции «&» над двумя числами (25 и 77 в двоичном представлении), которые имеют, например, 16 бит, получили новое число, т.е. 9.

Поразрядный оператор «&» часто используется для операций маскирования. С его помощью принудительно можно установить заданный бит данных в значение 0. Например, в утверждении

переменной w3 присваивается значение переменной w1 , для которой выполнена поразрядная операция & со значением 3. При этом все биты левее двух младших битов устанавливаются в 0, а остальные биты сохраняют свое значение [16.2]. Маска представляет собой некоторую комбинацию разрядов [16.1]. Разряды маски с нулевыми значениями можно считать аналогом непрозрачных ячеек реальной маски, а разряды со значениями 1 – прозрачными ячейками.

Поразрядная операция & называется также конъюнкцией, или логическим умножением. Применяется часто обозначение AND.

Поразрядная операция ИЛИ обозначается символом | .

Когда над двумя значениями производится операция поразрядно ИЛИ , то последовательно сравниваются значения всех битов при двоичном представлении этих значений [5]. Если при этом соответствующий бит имеет значение 1 в первом или втором операнде, то результирующее значение будет равно 1. Рассмотрим предыдущий пример с поразрядной операции ИЛИ :

Поразрядная операция ИЛИ (|)

w1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 (25)

w2 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 (77)

w3 0 0 0 0 0 0 0 0 0 1 0 1 1 1 0 1 (93)

Поразрядную операцию ИЛИ (|) обычно используют для установки заданных битов слова в 1. Логическую операцию ИЛИ называют также включающей дизъюнкцией, или логическим сложением. Часто применяется обозначение OR.

Поразрядная операция исключающего ИЛИ ( ^ ) работает следующим образом [5]. Сравниваются соответствующие биты двух операндов, и если только один из битов равен 1, то результат будет равен 1. А при равенстве обоих соответствующих битов или 0, или 1 результат будет равен 0. Для двух операндов b1, b2 при использовании исключающего ИЛИ ( ^ ) справедлива таблица истинности (табл. 16.3).

Таблица 16.3.

Таблица истинности операции исключающего ИЛИ ( ^ )
b1	b2	b1 ^ b2
0	0	0
0	1	1
1	0	1
1	1	0

Если операцию исключающего ИЛИ ( ^ ) использовать для одного и того же значения, то в результате будет получено нулевое значение. Этот прием часто использовался программистами на языке ассемблера как наиболее быстрый путь установить значение в нуль или сравнить два значения на их равенство. Этот способ не рекомендуется использовать в языке программирования С, так как при этом скорость работы не повышается, а программа становится менее понятной [16.2].

Операция исключающего ИЛИ ( ^ ) может применяться для перестановки значений двух переменных без выделения дополнительной памяти (и, соответственно, без использования дополнительной переменной).

Поразрядная операция исключающего «ИЛИ» называется также исключающей дизъюнкцией. Часто применяется обозначение XOR.