Что такое алгоритм

Алгоритмизация. Понятие алгоритма. Свойства и способы описания алгоритмов.

Все предметы / Программирование / Проектирование программного обеспечения / Алгоритмизация. Понятие алгоритма. Свойства и способы описания алгоритмов.

Решение задач с использованием компьютера основано на понятии алгоритма, который является точным описанием вычислительного процесса, ведущего от варьируемых начальных данных к конечному результату.

Алгоритмы заложены в основе каждой программы, а также они встречаются во многих сферах деятельности человека (например, рецепты, схема вязания или танца).

Алгоритмизация является техникой разработки алгоритма для решения задач на ЭВМ.

Алгоритм — это.

Алгоритмы окружают нас повсюду. По их принципам существует животный мир, люди, работают компьютеры и механизмы. Некоторые из них очевидны, другие же скрыты от глаз (но это не значит, что их нет).

Алгоритм в информатике — это последовательность действий, которая направлена на достижение окончательного решения проблемы наиболее оптимальными и эффективными способами.

Существует версия, что термин алгоритм произошел от имени древнего ученого Аль-Хорезми, который написал трактат «Книга о сложении и вычитании».

Позднее один из переводчиков на латинский язык неправильно перевел имя ученого и вынес его в название книги — «Алгоритмии о счете индийском». Так этот термин проник в европейские языки и закрепился в них.

Существуют сложные и легкие алгоритмы. Для решения одних не требуется усилий, а для других не хватит и всей мощности компьютеров.

Любые действия, предполагающие определенную последовательность в жизни животных и людей, можно назвать алгоритмом (поиск пищи для животного, поход в магазин за хлебом).

Конечно, животное, ищущее корм, не подозревает, что использует алгоритмы, но действует по определенным правилам (инстинктам), чтобы добыть пропитание:

1. животное ищет место, где есть корм (используя обоняние и другие органы чувств);
2. затем осуществляет действия, чтобы добраться до лакомства;
3. при удачном исходе съедает найденное.

В информатике и программировании алгоритмы используются для написания программ (что это такое?). Чем качественнее алгоритмы, используемые в программе, тем лучше она работает.

Когда вы начинаете изучать любой язык программирования, то первое, что вам объясняют — это принципы построения алгоритма для будущей программы. Это такие блок-схемы, которые наглядно покажут ход обработки данных и логику вычислений. Без них поначалу будет очень трудно писать программы.

Как все это делается и выглядит на практике отлично показано на приведенном выше видео. Не буду повторяться, а лишь настоятельно посоветую потратить десять минут на его просмотр.

Алгоритмы и способы их описания

Алгоритм — набор команд, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий.

Алгоритмы могут описывать процессы преобразования самых разных объектов. Само слово «алгоритм» происходит от «algorithmi» — латинской формы написания имени выдающегося математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических операций.

Свойства алгоритмов

1. Дискретность — алгоритм должен представлять процесс решения задачи как последовательное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно.

2. Детерминированность (определённость). В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных.

3. Понятность — алгоритм должен включать только те команды, которые доступны исполнителю и входят в его систему команд.

4. Завершаемость (конечность) — при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов.

5. Массовость (универсальность). Алгоритм должен быть применим к разным наборам исходных данных.

6. Результативность — завершение алгоритма определёнными результатами.

Основные принципы разработки алгоритмов.

Список литературы: 1. Основы программирования в среде Турбо Паскаль 7.0: Методические указания/ Рязан. гос. радиотехн. акад.; Сост. В.В. Белов, В.И. Чистякова. Рязань, 2005. 2. Новичков В.С., Панфилова Н.И., Пылькин А.Н. Алгоритмизация и программирование на Турбо Паскале: Учебное пособие. – М.: Горячая линия – Телеком, 2005. 3. Москвитина О.А., Новичков В.С., Пылькин А.Н. Сборник примеров и задач по программированию: Учебное пособие. – М.: Горячая линия – Телеком, 2007.

Основы алгоритмизации.

План.

1. Этапы решения задачи на ЭВМ.

2. Алгоритм и его свойства.

3. Способы записи алгоритмов.

4. Основные принципы разработки алгоритмов.

Этапы решения задачи на ЭВМ.

Работа по решению любой задачи с использованием компьютера делится на следующие взаимосвязанные этапы (приведенное разделение является условным):

1. Постановка задачи.

2. Формализация задачи.

3. Построение алгоритма.

4. Составление программы на языке программирования.

5. Отладка и тестирование программы.

6. Проведение расчетов и анализ полученных результатов.

Часто эту последовательность называют технологической цепочкой решения задачи на ЭВМ. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5.

На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения, здесь выясняется, существует ли решение поставленной задачи и единственно ли оно.

После постановки условия осуществляется «перевод» задачи на язык математики, то есть составляется система математических формул, уравнений, отношений, описывающих поведение исследуемого объекта, так получаем модель, которую обычно называют математической мо­делью. Таким образом, формализация равносильна получению соответствующей математической модели.

Третий этап — построение алгоритма. Данный этап заключается в разложении вы­числительного процесса на возможные составные части, установлении порядка их следования, описании содержания каждой такой части в той или иной форме и последующей проверке, которая должна показать, обеспечивается ли реализация выбранного метода. В большинстве случаев не удается сразу получить удовлетворительный результат, поэтому со­ставление алгоритма проводится методом проб и устранения ошибок и для получения окончательного варианта требуется несколько шагов коррекции и анализа.

Опытные программисты часто сразу пишут программы на языках, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования.

Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования.

Разра­ботанный на третьем этапе алгоритм решения задачи необходимо изложить на специальном, понятном ЭВМ языке, который называется языком программирования. Алгоритм, записанный на языке программирования, называется программой.

На пятом этапе выясняется правильность написания программы, выявляются смысловые и синтаксические ошибки и т. п. За­тем программа вводится в память ЭВМ и ошибки, оставшиеся незамеченными, выявляются уже непосредственно с помощью машины. На этом же этапе производят тестирование программы, то есть проверку при известных частных условиях.

Только после того как появится полная уверенность, что программа обеспечивает получение правильных результатов, можно приступать непосредственно к расчетам по программе. Последний шестой этап — это использование уже разработанной программы в практических целях.

Таким образом, программист должен обладать следующими знаниями и навыками:

• уметь строить алгоритмы;

• знать языки программирования;

• уметь работать в соответствующей системе программирования.

Алгоритм и его свойства.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi — латинского написания имени Мухаммеда аль-Хорезми (787—850), выдающегося арабского математика. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике. Правила алгебраических преобразований, способы вычислений корней уравнений также можно отнести к математическим алгоритмам.

В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем.

Далее, изучая понятие алгоритма, мы будем предполагать, что его исполнителем является автоматическое устройство, а именно компьютер. Это накладывает на запись алгоритма целый ряд обязательных требований. Сформулируем эти требования в виде перечня свойств, которыми должны обладать алгоритмы, адресуемые к исполнению на ЭВМ:

— Дискретность. Процесс решения задачи должен быть разбит на упорядоченную последовательность отдельных предписаний (правил, директив, команд), образующих прерывную (или, как говорят, дискретную) структуру алгоритма: только выполнив требования одного предписания можно присту­пить к исполнению следующего;

— Понятность. Исполнитель может выполнить алгоритм, если он ему понятен, т.е. записан на понятном ему языке и содержит предписания, которые исполнитель может выполнить. Набор действий, которые могут быть выполнены исполнителем, называются системой команд исполнителя. Алгоритм не должен содержать описания действий, не входящих в систему команд исполнителя.

— Детерминированность — это свойство определенности и однозначности. Алгоритмы, предназначенные для исполнения некоторым техническим устройством, не должны содержать предписаний, приводящих к неоднозначным действиям. Алгоритм рассчитан на чисто механическое исполнение, и если применять его повторно к одним и тем же исходным
данным, то всегда должен получиться один и тот же результат на каждом шаге алгоритма.

— Массовость — алгоритм должен разрабатываться сразу для общего случая решения задачи, должна иметьсявозможность получения результата при различных исходных данных на некоторой области допустимых значений.

— Конечность (результативность) – выполнение алгоритма решения задачи должно закончиться за конечное число шагов и должен быть получен конечный результат по поводу решения поставленной задачи.

— Эффективность. Эффективность алгоритма часто определяет возможность его практической реализации и может рассматриваться с разных позиций: с точки зрения времени выполнения, сложности, затраченных ресурсов, информационно-программного обеспечения.

Свойства массовости и эффективности не являются необходимыми свойствами алгоритма. Они скорее определяет качество алгоритма; в то же время свойства дискретности, понятности, детерминированности, результативности являются необходимыми (иначе это не алгоритм).

Перечисленные свойства алгоритма, по существу, являются нефор­мальным его определением. Объединяя их в одно целое, мы можем сфор­мулировать это определение следующим образом:

Алгоритм — это полное и точное описание конечной последовательности действий, которые исполнитель должен выпол­нить, чтобы за конечное время перейти от исходных дан­ных к искомому результату.

Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя в рамках его системы команд. Исполняя алгоритм, исполнитель не вникает в смысл того, что он делает, но вместе с этим он может получить нужный результат. В таких случаях говорят, что исполнитель действует формально. При программировании для ЭВМ исполнителем является компьютер. Точнее говоря, исполнителем является комплекс ЭВМ + Система программирования (СП). Программист составляет программу на том языке, на который ориентирована СП.

Способы записи алгоритмов.

В процессе разработки алгоритма могут использоваться различные способы его описания, отличающиеся по простоте, наглядности, ком­пактности, степени формализации, ориентации на машинную реализацию и другим показателям. В практике программирования наибольшее распространение получили:

— словесное описание (кулинарные рецепты);

— псевдокод, когда используется формальный алгоритмический язык;

— задание алгоритма в виде цепочки формул;

— графическое описание алгоритма в виде структурограммы или блок-схемы.

Изображение алгоритмов в виде структурограмм (схем Насси-Шнейдермана) пред­ставляет собой попытку использования требований структурного про­граммирования в схемах алгоритмов. Данный способ позволяет изображать схему пе­редач управления с помощью представления вложенности структур. Структурограммалучше отражает структуру алгоритма, чем блок-схема. Но для ее составления требуется много места.

Блок-схема – это наглядное графическое изображение алгоритма с элементами словесной записи, при котором отдельные действия (этапы) алгоритма изображаются при помощи различных геометрических фигур (блоков), а связи между этими этапами указываются при помощи стрелок, соединяющими эти фигуры. Различным (по типу выполняемых действий) блокам соответствуют различные геометрические фигуры. Приняты определенные стан­дарты графических изображений блоков:

Наименование символа	Обозначение	Назначение блока	Соответствующий оператор
Начало	Блок, обозначающий начало процесса обработки данных или выполнения алгоритма.	begin
Данные (ввод)	Блок ввода с клавиатуры исходной информации в ОП ЭВМ, внутри блока перечисляются вводимые данные.	readln()
Процесс	Блок обработки, внутри блока записываются операции, в результате которых изменяются значения, форма представления или расположение данных. В нем допускается запись самого оператора.	чаще оператор присваивания :=
Данные (вывод)	Блок автоматического вывода информации из ЭВМ на монитор, т.е. преобразования данных в форму, пригодную для отображения результатов обработки.	write() writeln()
Предопределенный процесс (подпрограмма)	Блок использования ранее созданных или отдельно описанных алгоритмов.	Имя подпрограммы с входными и выходными переменными
Логический блок	Блок выбора направления выполнения алгоритма в зависимости от некоторых условий (указываются внутри блока).	if .. then .. else .. while … do … repeat … until …
Модификация	Блок выполнения операции, меняющей значение параметра. Используется при описании циклических алгоритмов.	for … to …do … for. downto..do ..
Конец	Блок, обозначающий окончание, прерывание процесса обработки данных или выполнения алгоритма.	end

Рассмотрим алгоритм решения задачи определения наибольшего общего делителя (НОД) двух целых положительных чисел M, N, представленный различными способами.

Известен алгоритм решения этой задачи, получивший название алгоритм Евклида:

п 1. Если числа равны между собой, то взять в качестве НОД любое
из них.

п 2. Если числа не равны между собой, то большее из чисел заменить
их разностью и вернуться к п.1

Более детально алгоритм Евклида может быть представлен следую­щей словесной записью:

Пока M≠N, выполнять:

если М > N, то М := M-N; иначе N := N—M.

Структурограмма, блок-схема и запись на алгоритмическом языке данного алгоритма имеют соответственно вид:

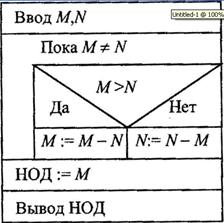
Для описания алгоритмов в дальнейшем мы будем использовать блок-схемы, поскольку они являются наглядным и простым способом представления алгоритмов. Их обычно используют на первом этапе алгоритмизации, при разработке общей структуры алгоритма, так как блок-схемы позво­ляют отчетливо представить себе алгоритм в целом и проследить все ло­гические связи между отдельными частями алгоритма, проверить все возможные варианты решения поставленной задачи и выявить допущен­ные ошибки или неточности. Для проверки правильности алгоритма может быть построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм.

Основные принципы разработки алгоритмов.

Прошло уже более полувека со времени появления первой ЭВМ. Все это время вычислительная техника бурно развивалась. Менялась элементная база ЭВМ, росли быстродействие, объем памяти, менялись средства взаимодействия человека с машиной. Безусловно, эти изменения сказывались самым непосредственным образом на работе программиста. Определенный общепринятый способ производства чего-либо (в данном случае — программ) называют технологией. Далее мы будем говорить о технологии программирования.

С ростом памяти и быстродействия ЭВМ, с совершенствованием языков программирования и трансляторов с этих языков проблема экономичности программы становится менее острой. Все более важной качественной характеристикой программ становится их простота, наглядность, надежность. С появлением машин третьего поколения эти качества стали основными.

В конце 60-х — начале 70-х гг. XX столетия вырабатывается дисциплина, которая получила название структурного программирования, в рамках которой сформировался так называемый структурный подход к конструированию и оформлению алгоритмов. Ее появление и развитие связано с именами Э. В. Дейкстры, Х.Д.Милса, Д. Е. Кнута и других ученых. Структурное программирование до настоящего времени остается основой технологии программирования. Соблюдение его принципов позволяет программисту быстро научиться писать ясные, безошибочные, надежные программы.

Структурный подход – это совокупность приемов и правил разработки алгоритмов, имеющих четкую и ясную структуру. Выделение четкой и ясной структуры алгоритма уменьшает количество ошибок на этапе разработки алгоритма, упрощает их контроль и модификацию. Алгоритм становится более удобным.

По своей сути структурный подход есть отказ от беспорядочного стиля в алгоритмизации (в частности, отказ от оператора GOTO) и опре­деление ограниченного числа стандартных приемов построения легко чи­таемых алгоритмов с ясно выраженной структурой. Теоретически фун­даментом этого подхода является теорема о структурировании (которая была строго доказана в теории программирования), из кото­рой следует, что алгоритм для решения любой логической задачи можно составить только из структур «следование, ветвление, цикл с предусловием». Их называют базовыми алгоритмическими структурами.

Однако с целью создания более компактных и наглядных алгорит­мов дополнительно используются следующие управляющие структуры: а) сокращенная запись ветвления; б) структура выбора; в) структура цик­ла с параметром; г) структура цикла с постусловием.

Следование — структура, реализующая вычислительный процесс, в котором отдельные этапы вычислений должны выполняться последовательно друг за другом. Это линейная последовательность действий, в которой каждый блок может содержать в себе как простую команду, так и сложную структуру, но обязательно должен иметь один вход и один выход.

Ветвление — структура, реализующая вычислительный процесс, в котором в зависимости от истинности или ложности условия должно выполняться либо одно, либо другое действие (управление передается одному из двух блоков), после чего происходит выход на общее продолжение.

Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется действие 1 — последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется действие 2 (отрицательная ветвь).

Действие 1 или действие 2 может в свою очередь содержать несколько этапов.

Сокращенная запись ветвления имеет место, когда на ветви «нет» пусто.

Вычислительные процессы с многократным повторением однотип­ных вычислений/действий для различных значений входящих вели­чин/данных называются циклическими, повторяемые участки вычисле­ний – циклами.

Для организации циклов в алгоритмах необходимо предусмотреть:

• подготовку цикла — задание начальных значений переменным цикла перед первым его выполнением;

• тело цикла — действия, повторяемые в цикле для различных значений переменных цикла;

• модификацию/изменение значений переменных цикла перед каждым новым его повторением;

• управление циклом — проверку условия продолжения/окончания цик­ла и переход на повторение цикла или его окончание.

Существует несколько видов циклов:

a. цикл с предусловием (цикл «пока») — когда цикл начинается с проверки условия продолжения цикла;

b. цикл с постусловием (цикл «до») — когда условие проверяется после выполнения тела цикла;

c. цикл с параметром – когда известно число повторений тела цикла.

Теоретически необходимым и достаточным является лишь первый тип цикла — цикл с предусловием. Любой циклический алгоритм можно построить с его помощью.

Цикл с предусловием применяется при необходимости выполнить какие-либо действия несколько раз, пока условие истинно. Особенность этого цикла в том, что он может не выполнится ни разу, так как первая проверка условия выхода из цикла происходит до того, как будет выполнено тело цикла. Тело цикла повторяет свое выполнение, если условие истинно. Повторение кончается, когда условие станет ложным.

Цикл с постусловием применяется при необходимости выполнить какие-либо действия несколько раз до выполнения некоторого условия. Особенность этого цикла в том, что он всегда выполняется хотя бы один раз, так как первая проверка условия выхода из цикла происходит после того, как тело цикла выполнено. Тело цикла повторяет свое выполнение, если условие ложно. Повторение кончается, когда условие станет истинным.

В циклах с параметром (с известным числом повторений) всегда можно определить переменную, связанную с числом повторений цикла, значение которой изменяется по заданному закону: от начального до конечного с постоян­ным шагом. Такая переменная используется для управления циклом: в условии окончания цикла осуществляется сравнение текущего значения переменной с заданным порогом. Эту переменную именуют параметром цикла.

Для схемного представления цикла с параметром используют специ­альную управляющую структуру с блоком модификации, где указывают закон изменения параметра цикла. Блок модификации включает в себя подготовку цикла (х := х_о), изменение параметра цикла при его очередном повторении (х :=х + h_x), управление циклом — проверку условия его продолжения (х ≤ х_к) и переход на про­должение или окончание цикла. Проверка условия х ≤ х„ проводится пе­ред каждым, в том числе первым, выполнением цикла, как в цикле с пре­дусловием. И если начальное значение параметра цикла больше конечно­го, то цикл не выполняется ни разу.

Множественный выбор явля­ется обобщением разветвления, когда в зависимости от значения выражения (i) вы­полняется одно из нескольких действий. При i=1 выполня­ется действие s1, при i=2— действие s2 и т. д., ), после чего происходит выход на общее продолжение.

Особенностью всех приве­денных структур является то, что они имеют один вход и один выход, и их можно соединять друг с другом в любой последовательности. В частности, каждая структура может содержать любую другую структуру в качестве одного из блоков. На основании этого можно сформулировать два основных приема использования базовых алгоритмических структур

a) присоединение – одна структура следует за другой (на блок-схеме – выход соединен со входом);

b) вложение – одна структура находится внутри другой (прямоугольник заменяется другой фигурой).

Структурный подход требует соблюдения стандарта в изображении блок-схем алгоритмов. Нестандартно изображенная блок-схема плохо читается, теряется наглядность алгоритма. Вот несколько примеров структурных блок-схем алгоритмов.

Такие блок-схемы легко читаются. Их структура хорошо воспринимается зрительно. Структуре каждого алгоритма можно дать название. У приведенных на рисунке блок-схем следующие названия:

1. Вложенные ветвления.

2. Цикл с вложенным ветвлением.

3. Вложенные циклы-пока.

4. Ветвление с вложенной последовательностью ветвлений на положительной ветви и с вложенным циклом-пока на отрицательной ветви.

5. Следование ветвления и цикла-до.

6. Вложенные циклы. Внешний — цикл-пока, внутренний — цикл-до.

Рассмотрим следующую задачу: дано целое положительное число п. Требуется вычислить n! (n-факториал). Вспомним определение факториала:

На рисунке приведена блок-схема алгоритма. В нем используются три переменные целого типа: п — аргумент; i — промежуточная переменная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая п = 3.

Трассировка доказывает правильность алгоритма.

Дополнительно: [2] стр. 5-53

Дата добавления: 2018-06-01 ; просмотров: 3753 ; Мы поможем в написании вашей работы!

© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.037)