Числа с плавающей точкой
Числа с плавающей точкой более или менее соответствуют тому, что математики называют «вещественными числами». Они включают в себя числа, расположенные между целыми. Вот некоторые из них: 2.75, 3.16Е7, 7.00 и 2е-8. Очевидно, что любое число с плавающей точкой можно записать несколькими способами. Более полное обсуждение «Е-нотации» будет проведено дальше, а мы только кратко поясним, что запись вида «3.16Е7» означает число, полученное в результате умножения 3.16 на 1,0 в седьмой степени, т. е. на 1 с семью нулями. Число 7 называется «порядком» (показателем степени при основании 10).
Наиболее существенным моментом здесь является то, что способ кодирования, используемый для помещения в память числа с плавающей точкой, полностью отличается от аналогичной схемы для размещения целого числа. Формирование представления числа с плавающей точкой состоит в его разбиении на дробную часть и порядок; затем обе части раздельно помещаются в память. Поэтому число 7.00 из вышеприведенного списка нельзя поместить в память тем же способом, что и целое число 7, хотя оба имеют одно и то же значение. В десятичной записи (точно так же как и в двоичной) число «7.0» можно было бы записать в виде «0.7Е1»; тогда «0.7» будет дробной частью, а «1» — порядком. Для размещения чисел в памяти машины будут, конечно, использоваться двоичные числа и степени двойки вместо степеней десяти. Дополнительную информацию, относящуюся к этому вопросу, вы сможете найти в приложении Ж. Здесь же мы остановимся лишь на различиях, связанных с практическим использованием чисел этих двух типов.
1. Целые числа не имеют дробной части, в то время как числа с плавающей точкой могут представлять как целые, так и дробные числа.
2. Числа с плавающей точкой дают возможность представлять величины из более широкого диапазона, чем целые (см. табл. 3.1).
3. При некоторых арифметических операциях, например при вычитании одного большого числа из другого, использование чисел с плавающей точкой приводит к большей потере точности.
4. Операции над числами с плавающей точкой выполняются, как правило, медленнее, чем операции над целыми числами. Однако сейчас уже появились микропроцессоры, специально ориентированные на обработку чисел с плавающей точкой, и в них эти операции выполняются довольно быстро.
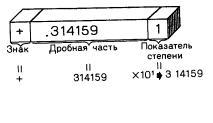
РИС. 3.3. Десятичное представление числа p в формате с плавающей точкой.
Возьмите некоторое число. Добавьте к нему 1, а затем вычтите из полученной суммы исходное число. Что у вас получится? У нас получилась 1. Но вычисления, производимые над числами с плавающей точкой, могут дать и совершенно неожиданный результат:
Причина появления такого странного результата состоит в отсутствии доста точного числа разрядов для выполнения операций с требуемой точностью. Число 2.0е20 записывается как двойка с последующими двадцатью нулями, и, до бавляя к нему 1, мы пытаемся изменить 21-ю цифру Чтобы выполнить эту oпe рацию корректно, программа должна иметь возможность поместить в память число, состоящее из 21 цифры. Но число типа float (т е. с плавающей точкой) путем изменения порядка можно увеличить или уменьшить лишь на 6 или 7 цифр. Попытка вычисления оказалась неудачной. С другой стороны, если бы мы использовали, скажем, число 2.0е4 вместо 2.0е20, мы смогли бы получить правильный ответ, поскольку в этом случае мы пытались бы изменить 5-ю цифру, и точность представления чисел типа float оказалась бы вполне достаточной для этого.
Нарушение свойства ассоциативности
Вычислим (sin(x)), разложив эту функцию в ряд Тейлора:
Напишем небольшую функцию, которая будет реализовывать эти вычисления. Тип float вместо double выбран для того, чтобы показать, как быстро накапливается погрешность; никаких дополнительных действий не производится, код исключительно демонстрационный. Целью не является показать, что семи членов ряда недостаточно, цель — показать нарушение свойства ассоциативности операций:
хотя свойство коммутативности сохраняется:
Теперь напишем аналогичную функцию, но сделаем так, чтобы те же элементы ряда суммировались в обратном порядке.
Посмотрим на это с точки зрения машины:
(sin(pi) approx 3141592 — 516771) (+ 255016) (- 0599265) (+ 00821459) (- 000737043) (+ 0000466303,)
(sin(pi) approx 0000466303 — 000737043) (+ 00821459) (- 0599265) (+ 255016) (- 516771) (+ 3141592.)
До этого момента мнение компьютера и человека, казалось бы, сходится. Но результатом в первом случае окажется (00000211327) ( (2.11327e005)), а во втором случае — (00000212193) ( (2.12193e005)), совпадают лишь две значащие цифры!
Разгадка проста: у чисел представленного ряда шесть различных ( двоичных) порядков: (1), (2), (1), (-1), (-4), (-8), (-12). Когда складываются ( вычитаются) два числа одного порядка или близких порядков, потери точности, как правило, небольшие. Если бы мы складывали огромное число и много маленьких чисел одного порядка, то мы заметили бы, что лучше в плане точности сперва сложить все маленькие числа, а затем уже прибавить большое. Рассмотрим обратный сценарий: сложим большое и первое маленькое число; поскольку порядки значительно различаются, маленькое число будет ( фигурально выражаясь) « раздавлено» большим из-за приведения порядков; получилось новое большое число, не очень точное, но пока ещё достаточно близкое к точному результату; к получившемуся большому числу прибавляем второе маленькое, порядки снова значительно различаются, снова маленькое число оказывается раздавленным, уже две « жертвы». И так далее. Погрешность накопилась достаточно большая.
Сложение ( вычитание) чисел с одинаковым порядком тоже не проходит без округлений, но погрешности, как правило, минимальны.
Немного истории
В 60-е и 70-е годы не было единого стандарта представления чисел с плавающей запятой, способов округления, арифметических операций. В результате программы были крайне не портабельны. Но еще большей проблемой было то, что у разных компьютеров были свои «странности» и их нужно было знать и учитывать в программе. Например, разница двух не равных чисел возвращала ноль. В результате выражения «X=Y» и «X-Y=0» вступали в противоречие. Умельцы обходили эту проблему очень хитрыми трюками, например, делали присваивание «X=(X-X)+X» перед операциями умножения и деления, чтобы избежать проблем.
Инициатива создать единый стандарт для представления чисел с плавающей запятой подозрительно совпала с попытками в 1976 году компанией Intel разработать «лучшую» арифметику для новых сопроцессоров к 8086 и i432. За разработку взялись ученые киты в этой области, проф. Джон Палмер и Уильям Кэхэн. Последний в своем интервью высказал мнение, что серьезность, с которой Intel разрабатывала свою арифметику, заставила другие компании объединиться и начать процесс стандартизации.
Все были настроены серьезно, ведь очень выгодно продвинуть свою архитектуру и сделать ее стандартной. Свои предложения представили компании DEC, National Superconductor, Zilog, Motorola. Производители мейнфреймов Cray и IBM наблюдали со стороны. Компания Intel, разумеется, тоже представила свою новую арифметику. Авторами предложенной спецификации стали Уильям Кэхэн, Джероми Кунен и Гарольд Стоун и их предложение сразу прозвали «K-C-S».
Практически сразу же были отброшены все предложения, кроме двух: VAX от DEC и «K-C-S» от Intel. Спецификация VAX была значительно проще, уже была реализована в компьютерах PDP-11, и было понятно, как на ней получить максимальную производительность. С другой стороны в «K-C-S» содержалось много полезной функциональности, такой как «специальные» и «денормализованные» числа (подробности ниже).
В «K-C-S» все арифметические алгоритмы заданы строго и требуется, чтобы в реализации результат с ними совпадал. Это позволяет выводить строгие выкладки в рамках этой спецификации. Если раньше математик решал задачу численными методами и доказывал свойства решения, не было никакой гарантии, что эти свойства сохранятся в программе. Строгость арифметики «K-C-S» сделала возможным доказательство теорем, опираясь на арифметику с плавающей запятой.
Компания DEC сделала все, чтобы ее спецификацию сделали стандартом. Она даже заручилась поддержкой некоторых авторитетных ученых в том, что арифметика «K-C-S» в принципе не может достигнуть такой же производительности, как у DEC. Ирония в том, что Intel знала, как сделать свою спецификацию такой же производительной, но эти хитрости были коммерческой тайной. Если бы Intel не уступила и не открыла часть секретов, она бы не смогла сдержать натиск DEC.
Подробнее о баталиях при стандартизации смотрите в интервью профессора Кэхэна, а мы рассмотрим, как выглядит представление чисел с плавающей запятой сейчас.
Хранение в памяти
В общем случае, формат с плавающей запятой хранится следующим образом:
| (s) | (q_) | (ldots) | (q_0) | (m_) | (ldots) | (m_0) |
Где (s) – знак числа ( (0) для (+) и (1) для (-) ), (q_ ldots q_0) – порядок, (m_ ldots m_0) – дробная часть мантиссы.
Число (a) , хранимое таким образом, можно вычислить как [a = (s) left(1+sum_^ m_i 2^ right) cdot 2^
Нормальная и нормализованная форма
Нормальной формой числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале [0; 1). Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать в 4 формах — 0,0001×10 0 , 0,001×10 −1 , 0,01×10 −2 , 0,1×10 −3 ), поэтому распространена также другая форма записи —нормализованная, в которой мантисса десятичного числа принимает значения от 1 (включительно) до 10 (не включительно), а мантисса двоичного числа принимает значения от 1 (включительно) до 2 (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме 0) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа 0 (а заодно и некоторых других полезных чисел, таких как и ).

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, «не число», получается как результат операций типа деления нуля на ноль) и .
| Название | Тип в языке программирования C | Диапазон | Биты мантиссы | Биты |
|---|---|---|---|---|
| Half precision | Нет | 6,10×10 -5 ..65504 | 10+1 | 16 |
| Single precision | float | 3,4×10 -38 ..3,4×10 38 | 23+1 | 32 |
| Double precision | double | 1,7×10 -308 ..1,7×10 308 | 52+1 | 64 |
Внутреннее представление
Число в форме с плавающей точкой представляет собой совокупность знака, порядка и мантиссы. В машинном представлении чисел с плавающей точкой нулевой бит всегда несет информацию о знаке числа: 0 соответствует плюсу и 1 — минусу. Следующие 7 битов отведены под характеристику, являющуюся внутренней формой представления порядка. Остальное место занимает мантисса.
Знак. Числа с плавающей точкой, одинаковые по абсолютной величине, но имеющие разные знаки, отличаются друг от друга во внутреннем представлении лишь содержимым знакового разряда. Заметим, что в случае двоичной целочисленной арифметики дело обстояло совсем не так: отрицательные числа представлялись в дополнительном коде. Для умножения числа, представленного в форме с плавающей точкой, на —1 достаточно лишь изменить значение его знакового разряда. Мантисса чисел с плавающей точкой во внутреннем представлении фактически представляет собой абсолютную величину мантиссы. Умножив С380315Е на —1, мы получим 4380315Е.
Характеристика. Поскольку характеристика представлена 7-раз-рядным двоичным числом, ее значение может находиться в пределах от 00 до 7F16 или от 0 до 12710. Если бы в поле характеристики записывался в явном виде порядок числа, то мы имели бы числа исключительно с положительными порядками. Для того чтобы получить возможность пользоваться и числами с отрицательными порядками, в поле характеристики записывают число, превосходящее истинное значение порядка на 6410. Такое представление порядка называется представлением относительно числа 64. Минимальное значение характеристики равно 00000002. Минимальное значение порядка на 64 меньше, т. е. равно — 64. Аналогично, поскольку максимальное значение характеристики равно 12710, то, значит, в машине могут представляться лишь числа, порядок которых не превышает 6310. Итак, в машине представимы числа с плавающей точкой, находящиеся в интервале от 16-61 до 16+03, т. е. приблизительно от 5.4Х10-78 до 7.2X10’*.
Найти значение характеристики, соответствующее данному значению порядка, можно так: сначала преобразовать исходное значение порядка в двоичную форму, а затем, используя арифметику дополнительных кодов, прибавить к нему 6410 = Ю000002. Например, если порядок равен 1310, то характеристика вычисляется так:
Аналогично, если порядок равен — 5, то характеристика
Отметим, что знак порядка может быть легко определен по первому биту характеристики: если этот бит равен 1, то порядок положителен, если 0 — то отрицателен. Это, возможно, несколько непривычно, но тем не менее это так.
Мантисса. ЭВМ Систем 360 и 370 предоставляют возможность выполнения арифметических операций над числами с плавающей точкой двух форматов. Короткие числа с плавающей точкой занимают 32 разряда, т. е. полное слово памяти. Под знак и характеристику отведено 8 разрядов; таким образом, короткие числа имеют 24-разрядную мантиссу. Длинные числа с плавающей точкой состоят из 64-х битов, т. е. занимают двойное слово. Мантисса таких чисел содержит 56 битов.
В гл. 2 мы видели, что многие десятичные дроби не могут быть точно представлены в виде конечных двоичных. Например,
Для того чтобы точно представить подобные числа в машине, требуется бесконечное количество разрядов, так как в двоичной форме они представляются в виде бесконечных периодических дробей. При представлении таких чисел в реальных машинах допускаются ошибки округления.
Конечно, чем больше разрядов отводится для представления числа, тем выше точность этого представления. В связи с этим обычно возникает вопрос, какова точность аппроксимации десятичных дробей двоичными?
Для ответа на этот вопрос выясним, насколько отличаются числа, не совпадающие только в последнем разряде. Если дробные части чисел состоят из N битов, то разница будет 2 — N . Изменяя содержимое последнего разряда 4-разрядного дробного числа, мы изменим его величину на 2 -4 =1/16. Оценить соответствующую величину десятичного приращения можно, решив уравнение
Решить это уравнение можно, взяв десятичный логарифм от обеих частей:
— х log10 = ~N log10 2; х = N log10 2
Возвращаясь к представлению чисел в виде коротких чисел с плавающей точкой, имеем x=0.3×24=7.2
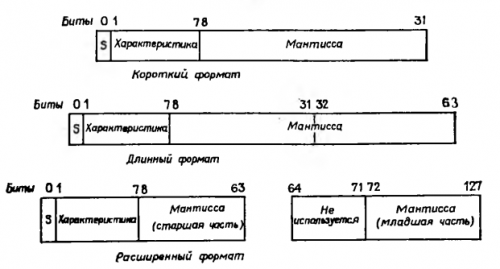
Рис. 19.1. Короткий, длинный и расширенный форматы чисел с плавающей точкой. S — бит знака.
Итак, используя 24 разряда для представления мантиссы чисел, мы получаем относительную точность их машинного представления в пределах 10 -7,2 . Другими словами, относительная точность представления чисел в случае одинарной точности (короткие числа с плавающей точкой) равна приблизительно 10 -7 . Аналогичные вычисления показывают, что при операциях удвоенной точности (длинные числа) можно получить относительную точность представления приблизительно 10 -18 . Мы получили оценки точности, обеспечиваемой при машинном представлении чисел с плавающей точкой. В дальнейшем мы увидим, что ошибки округления, возникающие при использовании арифметики с плавающей точкой, могут быть столь велики, что конечные результаты практически теряют всякий смысл.
Модель 85 Системы 360 и модели Системы 370 позволяют оперировать с числами, представленными в так называемом расширенном формате. С помощью такого формата достигается еще более высокая точность. Число, записанное в расширенном формате, занимает четыре полных слова. Первое двойное слово имеет тот же формат, что и в случае длинного числа. Однако знак и характеристика относятся ко всему 128-разрядному числу. На самом деле для записи числа используются только 120 разрядов, поскольку содержимое полей знака и характеристики второго двойного слова игнорируется. Итак, мантисса таких чисел имеет 128—16=112 разрядов. При этом относительная точность повышается до 10 -36 .
На рис. 19.1 изображены все форматы представления чисел с плавающей точкой в машинах фирмы IBM. Как же определить число по его внутреннему представлению? Для ответа на этот вопрос число разбивается на три части. Рассмотрим, например, короткое число
Поскольку нулевой бит равен 0, число положительно. Характеристика равна 43,в=6710; вычитая 64, получим значение порядка, равное 3. Мантисса равна .00С00016. Таким образом, искомое значение получится переводом числа
в десятичную форму. Окончательно получаем результат
.C00000X 161 = 1210
отрицательно, поскольку нулевой бит равен 1. Характеристика равна 25lg=3710, т. е. порядок равен —27,0. Получаем, что представленное число равно
Точно так же определяются значения чисел, представленных в двойном и расширенном форматах. Единственное отличие заключается в длине мантиссы.
Нормализация. Число с плавающей точкой называется нормализованным, если первая шестнадцатеричная цифра его мантиссы отлична от 0. На самом деле в нормализованном виде числа представляются наиболее точно, поскольку реально используются все разряды мантиссы. Рассмотрим нормализованное представление в коротком формате числа .2. Оно выглядит так:
Точность чуть больше чем 10~7. В ненормализованном виде это же число может быть записано, например, как
В данном случае реально используется всего 12 из 24 двоичных разрядов мантиссы. Теперь уже точность представления оказывается меньше 10-4. Аналогичные рассуждения можно провести относительно длинных и расширенных чисел. Использование ненормализованных чисел обычно ведет к уменьшению общей точности вычислений.
Для нормализации числа нужно выполнят^ последовательные сдвиги его мантиссы на четыре двоичных разряда каждый раз с одновременным вычитанием 1 из характеристики до тех пор, пока первая шестнадцатеричная цифра мантиссы не окажется отличной от 0. Нормализовав длинное число
Значение характеристики числа во время нормализации уменьшилось на поскольку было выполнено три 4-разрядных сдвига мантиссы. В процессе нормализации младшие разряды заполнились нулями. При выполнении арифметических операций, как мы увидим в дальнейшем, дело обстоит несколько сложнее, чем здесь описано.
Представление IEEE с плавающей запятой
Стандарт IEEE с плавающей запятой

Форма приблизительно представляет собой число. И разделите битовое представление числа с плавающей запятой на три поля:
Знак s определяет, является ли число отрицательным (s = 1) или положительным (s = 0). Символ s можно напрямую закодировать с помощью одного символа s.

Знаковое выражение M является десятичным двоичным числом и имеет диапазон 1 2-ξ или 0 ~ 1-ξ.
n-значное десятичное поле Кодировка мантиссы М.

Функция показателя степени E заключается в взвешивании числа с плавающей запятой. Этот вес представляет собой степень E числа 2 (может быть отрицательным числом). k-битное поле кода заказа Код заказа кодирования E.
В формате с плавающей запятой одинарной точности (float на языке C) поля s, exp и frac имеют размер 1, 8 и 23 бита соответственно, а в формате с плавающей запятой двойной точности (double на языке C) s, exp и Поле гидроразрыва составляет 1, 11 и 52 бита соответственно.
Общие биты числа с плавающей запятой представлены следующим образом:
По значению exp закодированное значение можно разделить на три различных ситуации. Объясняется одно за другим ниже.
Случай 1: нормализованное значение

То есть наиболее распространенный случай, когда exp, домен кода заказа — это не все нули и не все единицы. В этом случае поле кода заказа интерпретируется как целое число со знаком в предвзятой форме, то естьE=exp-Bias, exp — это беззнаковое число (1 ~ 254). Смещение равно Для одинарной точности k = 23 и Bias = 127, поэтому диапазон E составляет -126 ~ + 127.
Случай 2: денормализованное значение
Когда exp, то есть домен кода заказа равен 0, представленное число является ненормализованным значением, значение кода заказа в этом случаеE=1-Bias(Примечание: предоставляется метод преобразования неформатированного значения в форматированное значение). мантиссаM=frac
Денормализованные числа служат двум целям.
Представляет значение 0. В форматированных числах мы всегда делаем M≥1, поэтому 0 не может быть представлен. Когда код заказа равен 0, а мантисса также равна 0, он может представлять 0.
Представляет число, близкое к 0,0. Значение, которое он представляет, распределяется близко к 0,0, и атрибут постепенно переполняется.
Случай 3: Особое значение
Код заказа — все 1, а десятичное поле — все 0. Он получает значение + ∞ (s = 0) или -∞ (s = 1), которое может представлять результат переполнения в компьютере, например, умножение двух очень больших чисел.
Код заказа — все 1, а десятичное поле — не все 0. Он получает значение NaN (обратите внимание на число). Он может представлять недопустимые числа в компьютере, например значение при вычислении корневого числа -1.












