N 1 факториал как разложить

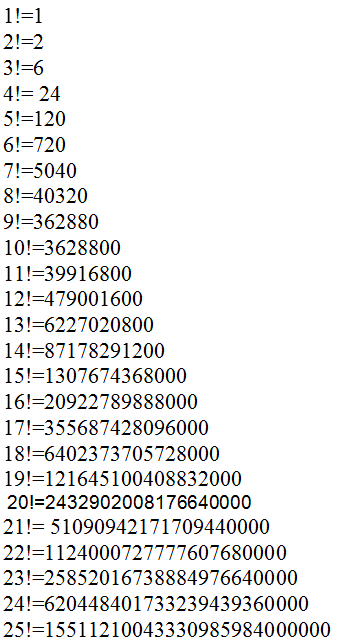
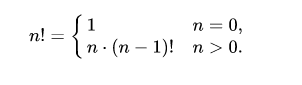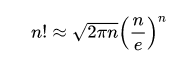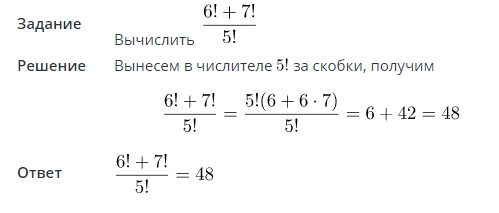Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.

Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.

Наивный алгоритм

Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:

На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.

Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.

Алгоритм вычисления деревом

Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.

Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).

Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):

P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800

Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне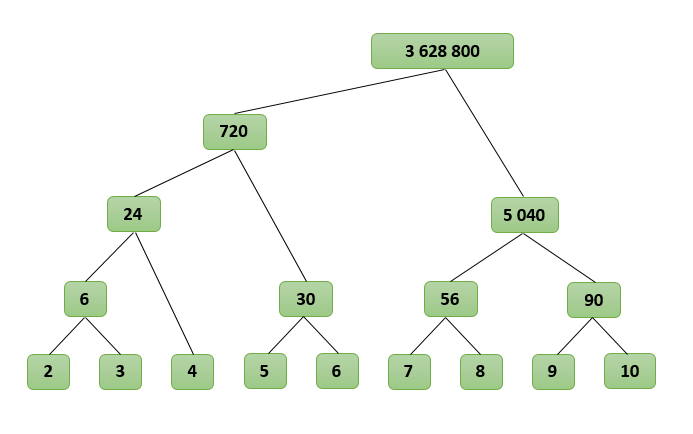

Реализуем описанный алгоритм:

Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.

Алгоритм вычисления факторизацией

Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…

Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.

Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:

10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800

Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:

Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!

Библиотека GMP

Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.

Сравнение производительности

Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.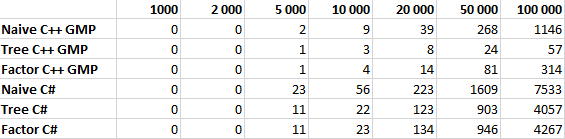

График с линейной шкалой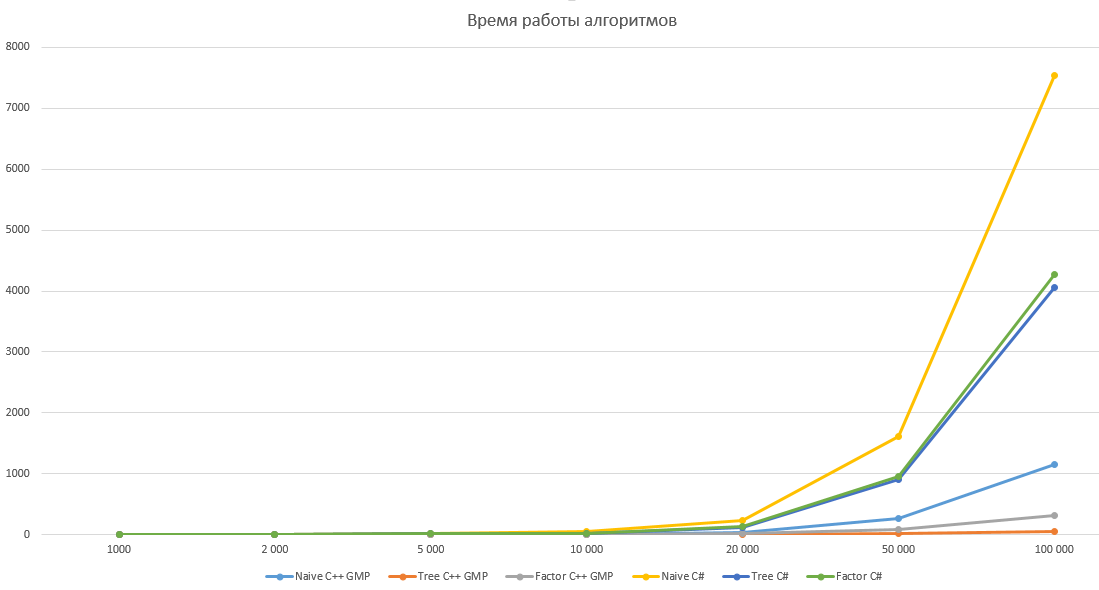

График с логарифмической шкалой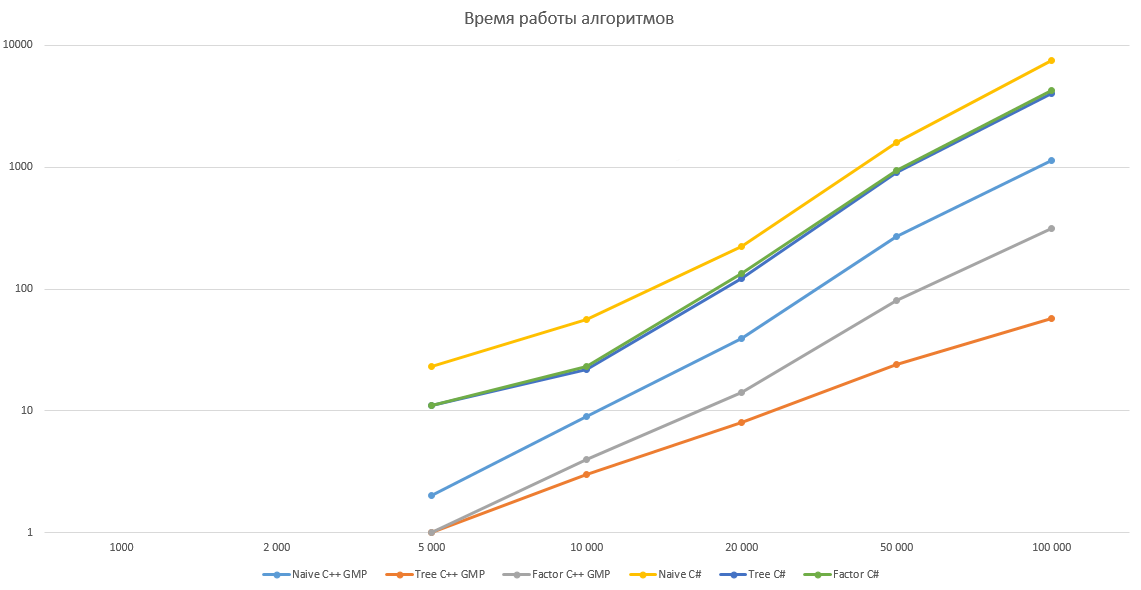

Идеи и алгоритмы из комментариев

Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них

Исходные коды

Исходные коды реализованных алгоритмов приведены под спойлерами

N 1 факториал как разложить

Факториал – так называют часто встречающуюся в практике функцию, определённую для целых неотрицательных чисел. Название функции происходит от английского математического термина factor – «сомножитель». Обозначается она n!. Знак факториала «!» был введён в1808 году во французском учебнике Хр. Крампа.

Для каждого целого положительного числа n функция n! равна произведению всех целых чисел от 1 до n.

Для удобства полагают по определению 0! = 1. О том, что нуль – факториал должен быть по определению равен единице, писал в 1656 году Дж. Валлис в «Арифметике бесконечных».

Функция n! растёт с увеличением n очень быстро. Так,

При преобразовании выражений, содержащих факториал, по лезно использовать равенство

(n + 1)! = (n + 1) • n! = (n + 1) • n • (n – 1)! (1)

Английский математик Дж. Стирлинг в 1970г. предложил очень удобную формулу для приближённого вычисления функции n!:

где е = 2,7182. — основание натуральных логарифмов.

Относительная ошибка при пользовании этой формулой очень невелика и быстро падает при увеличении числа n.

Способы решения выражений, содержащих факториал, рассмотрим на примерах.

Пример 2. Вычислить 10! 8!

Решение. Воспользуемся формулой (1):

Решение. Согласно формуле (1) имеем

Раскрыв скобки в произведении, получаем квадратное уравнение

n 2 + 5n — 84 = 0, корнями которого являются числа n = 7 и n = -12. Од нако факториал определен только для неотрицательных целых чисел, т. е. для всех целых чисел n ≥ 0. Поэтому число n = -12 не удовлетворя ет условию задачи. Итак, n = 7.

Пример 4. Найти хотя бы одну тройку натуральных чисел х, у и z, для которой верно равенство х! = y! • z!.

Решение. Из определения факториала натурального числа n сле дует, что

Положим в этом равенстве n + 1 = у! = х, где у — произвольное нату ральное число, получим

Теперь видим, что искомые тройки чисел можно задать в виде

где y- натуральное число, больше 1.

Например, справедливы равенства

Пример 5. Определить, сколькими нулями оканчивается деся тичная запись числа 32!.

Решение. Если десятичная запись числа Р = 32! оканчивается k нулями, то число Р можно представить в виде

где число q не делится на 10. Это означает, что разложение числа q на простые множители не содержит одновременно 2 и 5.

Поэтому, чтобы ответить на поставленный вопрос, попробуем опреде лить, с какими показателями в произведение 1 • 2 • 3 • 4 • . • 30 • 31 • 32 входят числа 2 и 5. Если число k — наименьший из найденных показателей, то число Р будет оканчиваться k нулями.

Итак, определим, сколько чисел среди натуральных чисел от 1 до 32 делятся на 2. Очевидно, что их количество равно 32/2 = 16. Затем определим, какое количество среди найденных 16 чисел делится на 4; затем — какое количество из них делится на 8 и т. д. В результате получим, что среди тридцати двух первых натуральных чисел на 2 делится 16 чисел,

из них на 4 делятся 32/4 = 8 чисел, из них на 8 делятся 32/8 = 4 числа, из них на 16 делятся 32/16 = 2 числа и, наконец, из них на 32 делятся 32/32=1, т.е. одно число. Понятно, что сумма полученных количеств:

16 + 8 + 4 + 2 + 1 = 31

равна показателю степени, с которым число 2 входит в 32!.

Аналогично определим, сколько чисел среди натуральных чисел от 1 до 32 делятся на 5, а из найденного количества на 10. Разделим 32 на 5.

Получим 32/5 = 6,4. Следовательно, среди натуральных чисел от 1 до 32

существует 6 чисел, которые делятся на 5. Из них на 25 делится одно

число, так как 32/25 = 1,28. В результате число 5 входит в число 32! с пока зателем, равным сумме 6+1 = 7.

Из полученных результатов следует, что 32!= 2 31 • 5 7 • т, где число т не делится ни на 2, ни на 5. Поэтому число 32! содержит множитель

10 7 и, значит, оканчивается на 7 нулей.

Итак, в данном реферате определено понятие факториала.

Приведена формула английского математика Дж Стирлинга для приближённого вычисления функции n!

При преобразовании выражений, содержащих факториал, по лезно использовать равенство

(n + 1)! = (n + 1) • n! = (n + 1) • n • (n – 1)!

На примерах подробно рассмотрены способы решения задач с факториалом.

Факториал используется в различных формулах в комбинаторике, в рядах и др.

Например, количество способов выстроить n школьников в одну шеренгу равняется n!.

Число n! равно, например, количеству способов, которыми можно n различных книг расставить на книжной полке, или, например, число 5! равно количеству способов, которыми пять человек можно рассадить на одной скамейке. Или, например, число 27! равно количеству способов, которыми наш класс из 27 учеников можно выстроить в ряд на уроке физкультуры.

Факториал числа $n!$ равен произведению чисел от 1 до $n$. Например, $5! = 1cdot 2cdot 3cdot 4cdot 5$. Для решения примеров на пределы с факториалами понадобится знать и понимать формулу разложения на множители. $$ (n+1)! = n!(n+1) qquad (1) $$

Например, $5! = 4! cdot 5 $, или $5! = 3! cdot 4 cdot 5$, а можно еще так $5! = 2! cdot 3 cdot 4 cdot 5 $.

Основная суть идеи:

Выносим наименьший факториал числа за скобки в числителе и знаменателе
Сокращаем факториалы, избавляя тем самым предел от них
Вычисляем предел подходящим способом

Пример 1

Вычислить предел с факториалами $lim_limits frac $

Решение

Подставляя $x=infty$ в предел получаем неопределенность бесконечность делить на бесконечность. Избавимся от факториалов. Для этого используем формулу (1) для их разложения на множители.

Подставляем в предел полученное выражение и сокращаем на $n!$ числитель со знаменателем.

Теперь подставляя бесконечность в предел вычисляем ответ.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ $$lim_limits frac = 0 $$

Определяем наименьший факториал $(2n+1)!$. Его нужно вынести за скобки. Но перед этим нужно разложить остальные факториалы на множители, одним из которых будет $(2n+1)!$. Для этого воспользуемся формулой (1).

$$(2n+2)! = (2n+1)! cdot (2n+2) $$ $$ (2n+3)! = (2n+1)! cdot (2n+2)cdot(2n+3) $$

Выполняем замену в пределе на полученные выражения.

Выносим общий множитель с факториалом в числителе за скобки и выполняем сокращение со знаменателем.

Раскрываем полученные скобки и сокращаем на $2n+3$.

Пример 2

Решить предел с факториалом $ lim_limits frac $

Решение

Ответ

$$ lim_limits frac = 0 $$

Понятно, что предел имеет неопределенность $frac $. Попробуем её устранить избавившись от факториалов. Сразу находим среди них наименьший $n!$. Его нужно будет вынести за скобки. Но перед этим остальные факториалы нужно разложить по формуле (1) и затем подставить в предел.

Далее раскрываем скобки, попутно упрощая выражения, и затем выносим $n$.

Осталось выполнить сокращение на $n$ и получить ответ.

Название темы, для несведующих людей, может быть немного запутанным, и даже похже на тафтологическое выражение «масло масленное». На самом деле, под название темы подразумевается разложение факториала на простейшие множители с степенями.

Кто сталкивался с факториалами, знают что уже при значении 20, факториал достигает огромных значений 2432902008176640000

При факториале 100 значение получается еще больше, и возникает резонный вопрос а как можно представить факториал такого числа в более удобной и наглядной форме? Во первых это красиво, а во вторых полезно, так как отвечает еще и на попутно возникающий вопрос, например , сколько двоек/пятерок/семерок в факториале числа 2015?

Что бы решить такую задачу, не надо вычислять факториал от числа 2015, а потом искать число целочисленных делений на тройку например , достаточно знать формулу по который рассчитывается число вхождений.

Итак если число p простое, то количество вхождений в факториал числа m, вычисляется как

где квадратные скобки означают что берётся целая часть от деления.

Самый простой пример, сколько раз входит число 3 в факториал 50?

то есть тройка встречается в числе 50! ровно 22 раза.

Теперь несложно, пробежавшись по всем простым числам от 1 до 50, для каждого из них узнать количество вхождений.

Окончательный ответ, в виде факторизации факториала пятидести будет иметь вид.

Решим еще один пример, часто встречающийся.

На какое количество нулей оканчивается факториал числа 306?

Для решения такой задачи надо знать что 10 это произвдение двух простых чисел 2 и 5.

Таким образом узнав количество вхождений пятерки в факториал ( количество вхождений двойки, естественно будет больше), мы узнаем какое количество нулей будет в факториала 306.

Ответ: на 75 нулей будет оканчиватся заданный факториал.

Факториал — формула, свойства и примеры решений

Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел.

Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.

Это очень просто, вот пример:

7! = 1 * … * 7 = 5040.

Факторизация — разложение функции на множители.

Таблица факториалов

Свойства факториалов

Рекуррентная формула

Комбинаторная интерпретация

Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.

Формула Стирлинга

Позволяет не перемножать большие числа. Обычно необходим только главный член:

Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.

Расчет по предыдущему значению

Функцию легко вычислить из предыдущего значения:

А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.

Однако было решено, что в случае 0 результат будет равен 1.

Некоторые очень большие значения

Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.

Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.

Примеры вычисления факториалов больших чисел:

70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);

100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;

200! это примерно 7 88657867867364479050355236321393 x 103743.

Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.

Программа на языке Паскаль:

На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.

Факториал дроби (½) — это половина квадратного корня pi = (½)√π.

Примеры задач с решениями

Задание 1

Задание 2

Использование факториалов

Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).

Факториал — формула, свойства и примеры решений

Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел.

Это очень просто, вот пример:

7! = 1 * … * 7 = 5040.

Факторизация — разложение функции на множители.

Таблица факториалов

Свойства факториалов

Рекуррентная формула

Комбинаторная интерпретация

Формула Стирлинга

Позволяет не перемножать большие числа. Обычно необходим только главный член:

Расчет по предыдущему значению

Функцию легко вычислить из предыдущего значения:

Однако было решено, что в случае 0 результат будет равен 1.

Некоторые очень большие значения

Примеры вычисления факториалов больших чисел:

70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);

100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;

200! это примерно 7 88657867867364479050355236321393 x 103743.

Программа на языке Паскаль:

Факториал дроби (½) — это половина квадратного корня pi = (½)√π.

Примеры задач с решениями

Задание 1

Задание 2

Использование факториалов

Двойной факториал

Двойной факториал неотрицательного целого числа n является произведением всех целых чисел от 1 до n, имеющих одинаковую четность (нечетную или четную) с n. Это также называется полуфакториалом числа и обозначается как !! , Например, двойной факториал 9 равен 9 * 7 * 5 * 3 * 1, что составляет 945. Обратите внимание, что следствием этого определения является 0 !! = 1

Примеры:

Для четного n двойной факториал равен:

Для нечетного n двойной факториал равен:

Рекурсивное решение:
Двойной факториал можно рассчитать по следующей рекурсивной формуле.

Ниже приводится реализация двойного факториала.

// функция для поиска двойного факториала заданного числа

unsigned int doublefactorial(unsigned int n)

printf ( «Double factorial is %d» , doublefactorial(5));

// функция для поиска двойного факториала

static long doublefactorial( long n)

return n * doublefactorial(n — 2 );

static public void main (String[] args)

System.out.println( «Double factorial»

+ » is » + doublefactorial( 5 ));

// Этот код предоставлен anuj_67.

# функция, чтобы найти двойной
# факториал заданного числа

if (n = = 0 or n = = 1 ):

return n * doublefactorial(n — 2 );

print ( «Double factorial is» ,

# Этот код добавлен
# от Smitha

// функция для поиска двойного факториала

static uint doublefactorial( uint n)

return n * doublefactorial(n — 2);

static public void Main ()

Console.WriteLine( «Double factorial»

// Этот код предоставлен anuj_67.

// PHP-код для
// Двойной факториал

// возврат функции
// двойной факториал

function doublefactorial( $n )

return $n * doublefactorial( $n — 2);

echo «Double factorial is » ,

// Этот код предоставлен Ajit.
?>

Итеративное решение:
Двойной факториал также может быть вычислен итеративно, поскольку рекурсия может быть дорогостоящей для больших чисел.

// функция для поиска двойного факториала заданного числа

unsigned int doublefactorial(unsigned int n)

for ( int i=n; i>=0; i=i-2)

printf ( «Double factorial is %d» , doublefactorial(5));

// Java-программа для поиска двойного факториала
// данного числа

// функция для поиска двойного факториала

static int doublefactorial( int n)

for ( int i = n; i >= 0 ; i = i- 2 )

public static void main(String[] args)

System.out.println( «Double factorial»

+ » is » + doublefactorial( 5 ));

// Этот код предоставлен Anuj_67

# Python3 Программа для поиска двойных
# факториал заданного числа

# Функция найти двойник
# факториал заданного числа

for i in range (n, — 1 , — 2 ):

if (i = = 0 or i = = 1 ):

print ( «Double factorial is» ,

# Этот код предоставлен mits

// C # Программа для поиска двойного факториала
// данного числа

// функция для поиска двойного факториала

static int doublefactorial( int n)

for ( int i = n; i >= 0; i = i-2)

static void Main()

Console.Write( «Double factorial»

// Этот код предоставлен Anuj_67

// функция для поиска двойного
// факториал заданного числа

function doublefactorial( $n )

for ( $i = $n ; $i >= 0; $i = $i — 2)

if ( $i == 0 or $i == 1)

echo «Double factorial is » , doublefactorial(5);

// Этот код предоставлен anuj_67.
?>

Выход:

Временная сложность указанных решений составляет O (n).

Важные моменты :

Двойной факториал и факториал связаны с использованием приведенной ниже формулы.
Двойной факториал часто используется в комбинаторике. Обратитесь к вики для получения списка приложений. Примером приложения является подсчет совершенных совпадений полного графа K _{n + 1} для нечетного n.

Эта статья предоставлена Рахул Агравал . Если вы как GeeksforGeeks и хотели бы внести свой вклад, вы также можете написать статью с помощью contribute.geeksforgeeks.org или по почте статьи contribute@geeksforgeeks.org. Смотрите свою статью, появляющуюся на главной странице GeeksforGeeks, и помогите другим вундеркиндам.

Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.