Типы переменных. Целые и вещественные переменные, представление целых и вещественных чисел в компьютере
Аннотация: Определяется понятие типа переменной как множества значений, которые она может принимать, и набора операций, которые можно совершать со значениями. Рассматриваются наиболее важные базовые типы алгоритмического языка — целые и вещественные числа. Подчеркивается особенность представления целых чисел в компьютере как элементов кольца вычетов, рассматривается интерпретация элементов кольца вычетов как неотрицательных чисел или чисел со знаком. Приводится представление вещественных чисел в компьютере в плавающей форме, рассматриваются особенности арифметики плавающих чисел.
Тип переменной определяется множеством значений, которое она может принимать. Кроме того, тип определяет операции , которые возможны с переменной. Например, с численными переменными возможны арифметические операции , с логическими — проверка, истинно или ложно значение переменной , с символьными — сравнение, с табличными (или массивами) — чтение или запись элемента таблицы с заданным индексом и т.п. Как правило, в любом современном языке имеется базовый набор типов и несколько конструкций, которые позволяют строить новые типы из уже созданных. Наборы базовых типов и конструкций различаются для разных языков. В описании неформального алгоритмического языка будут использоваться типы и конструкции, которые присутствуют в большинстве языков практического программирования.
Представление чисел
Сначала поясним на образном примере, что такое дискретность.
Дискретное множество состоит из отделенных друг от друга элементов. Например, песок дискретен, поскольку он состоит из отдельных песчинок. А вода или масло непрерывны (в рамках наших ощущений, поскольку отдельные молекулы мы всё равно ощутить не можем). Этот пример нужен нам только для аналогии. Здесь мы не станем углубляться в изучение материального мира, а вернемся к предмету изучения информатики — информации.
Самым традиционным видом данных, с которым работают компьютеры, являются числа. ЭВМ первого поколения умели решать только математические задачи. Люди начали работать с числами еще с первобытных времен. Первоначально человек оперировал лишь целыми положительными (натуральными) числами: 1, 2, 3, 4, . . Очевидно, что натуральный ряд — это дискретное множество чисел.
В математике ряд натуральных чисел бесконечен и не ограничен. С появлением в математике понятия отрицательного числа (Р. Декарт, XVII век в Европе; в Индии значительно раньше) оказалось, что множество целых чисел не ограничено как «справа», так и «слева». Покажем это на числовой оси (рис. 1.6), символы оо обозначают бесконечность.

Рис. 1.6. Математическое множество целых чисел на числовой оси
Из сказанного следует вывод: множество целых чисел в математике дискретно и не ограничено. Отметим еще один факт: разность соседних чисел натурального ряда (данного и предыдущего) всегда равна единице. Эту величину назовем шагом числовой последовательности.
Любое вычислительное устройство (компьютер, калькулятор) может работать только с ограниченным множеством целых чисел. Возьмите в руки калькулятор, на индикаторном табло которого помещается 10 знаков. Самое большое положительное число, которое на него поместится:

Самое большое по абсолютной величине (модулю)

Аналогично дело обстоит и в компьютере.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
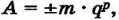
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
САМОЕ ГЛАВНОЕ
В математике множество целых чисел дискретно, бесконечно и не ограничено.
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. В любом случае компьютерное представление целых чисел дискретно, конечно и ограничено.
В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.
Для компьютерного представления вещественных чисел используется нормализованная запись вещественного числа а = ± m • q p , где q — основание системы счисления, р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ? m < q.
Компьютерное представление вещественных чисел дискретно, конечно и ограничено.
Практические примеры
В числах одинарной точности:
на знак отводится 1 бит, на экспоненту — 8, на мантиссу — 23.
В нормализованных числах старший бит всегда равен единице и он не записывается в число, поэтому реально мантисса для таких чисел имеет размер 24 бита.
К экспоненте перед записью добавляется число 127.
Для начала запишем знак числа. Если число положительное — запишем в знак 0, если отрицательное — 1 и отбросим знак числа для дальнейших вычислений.
Далее приведем число к такому виду, что перед запятой в двоичной записи у него только единица (если изначальное число 0 — оно имеет специальную запись 0 00000000 00000000000000000000000₂)
Для этого либо умножаем число на 2 пока оно не станет >= 1, если оно меньше 1, либо делим на 2 пока оно все еще >= 1.
Если умножаем — в экспоненту пойдет отрицательное число умножений.
Если делим — положительное число делений.
Потом получившееся число умножаем на 2²³ (8388608), округляем до ближайшего целого и отбрасываем старший бит. Результат записываем в мантиссу.
Пример 1
0,5 — положительное, в знак 0
0,5 < 1, умножаем его на 2, пока оно не станет >= 1. получилось 1 за 1 умножение. в экспоненту пойдет -1
мантисса = 1*8388608 = 100000000000000000000000₂
отбрасываем старший бит. получается 000000000000000000000000₂
записываем:
знак = 0 (число положительное)
в экспоненте 127 — 1 = 126 = 01111110₂
в мантиссе 000000000000000000000000₂
(без старшей единицы),получаем:
0 01111110 00000000000000000000000₂
Пример 2
25,12 положительное. в знак 0
25,12 делим на 2, пока >= 1. получаем 1,57 за 4 деления (если поделим еще раз, будет уже 0,785 < 1). в экспоненту пойдет +4.
1,57 * 8388608 = 13170114,56. округляем, получаем 13170115 = 110010001111010111000011₂
отбрасываем старший бит, получаем 10010001111010111000011₂
записываем
знак = 0
экспонента = 127+4 = 10000011₂
мантисса = 10010001111010111000011₂
получаем:
0 10000011 10010001111010111000011₂
-25,12 отрицательное, записываем в знак единицу, далее отбрасываем знак числа и считаем ровно как в предыдущем примере
1 10000011 10010001111010111000011₂
Пример 3
-3456,1. в знак единица, отбрасываем знак.
3456,1 > 1. делим на 2¹¹. получаем 1.687548828125, в экспоненту 11
1.687548828125 * 8388608 = 14156185.6.
округляем. 14156186 = 1101 1000 0000 0001 1001 1010₂, отбрасываем старшую единицу: 101 1000 0000 0001 1001 1010₂
знак 1
экспонента 127 + 11 = 10001010₂
мантисса 10110000000000110011010₂
результат 1 10001010 10110000000000110011010₂
Больше интересных статей читай по хэштегу #article@physics_math в группе Physics.Math.Code.Books Помощь и репетиторов по физике, высшей математике, программированию, информатике, иностранным языкам Вы найдете в Репетитор | IT mentor Наш канал в telegram : @physics_lib
Основные понятия и положения
Прежде чем начать разбираться в теме, следует понимать, что все ЭВМ, на данный момент времени, работают с двоичной системой счисления. Это значит, что и вся информация (звуковая, графическая или текстовая) хранится в памяти ПК в виде последовательностей нулей и единиц.
Схематично компьютерная память выглядит так, как показано на схеме ниже:

Как видно из рисунка внутренняя память представляет собой разряды, каждый из которых содержит один бит информации (0 или 1). А восемь битовых кластеров образуют один байт (машинное слово).
Машинное слово – минимально адресуемая ячейка памяти, которую за раз можно обработать командой процессора. То есть минимально процессор может обработать один байт.
Отсюда также вытекает правило, что данные в компьютере представляются дискретно (отдельно). В качестве примера приведем изображение на мониторе. Оно состоит из точек (пикселей). Цвет же каждой точки задается последовательностью из 0 и 1.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.



Алгоритм получения представления вещественного числа в памяти ЭВМ
Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина это типа занимает в памяти 8 байт. На рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| S | Смещенный порядок | Мантисса |
| 63 | 62..52 | 51..0 |
Можно заметить, что старший бит, отведенный под мантиссу, имеет номер 51, т.е. мантисса занимает младшие 52 бита. Черта указывает здесь на положение двоичной запятой. Перед запятой должен стоять бит целой части мантиссы, но поскольку она всегда равна 1, здесь данный бит не требуется и соответствующий разряд отсутствует в памяти (но он подразумевается). Значение порядка хранится здесь не как целое число, представленное в дополнительном коде. Для упрощения вычислений и сравнения действительных чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к настоящему значению порядка перед записью его в память прибавляется смещение. Смещение выбирается так, чтобы минимальному значению порядка соответствовал нуль. Например, для типа Double порядок занимает 11 бит и имеет диапазон от 2 -1023 до 2 1023 , поэтому смещение равно 1023(10) = 1111111111(2). Наконец, бит с номером 63 указывает на знак числа.
Таким образом, из вышесказанного вытекает следующий алгоритм для получения представления действительного числа в памяти ЭВМ:












