1.2.2. Представление вещественных чисел

Тест по информатике Представление чисел в компьютере для 8 класса

Тест по информатике Представление чисел в компьютере для 8 класса с ответами. В тесте 2 варианта, каждый включает в себя 7 заданий.

1. Если число положительное, то в знаковый разряд помещается

2. Числом в нормальной форме с нормализованной мантиссой (правильной дробью, имеющей после запятой цифру, отличную от нуля) является:

1) 0,341 x 10 9
2) 1997
3) 213,5629
4) 0,002311

3. Беззнаковым 8-разрядным представлением числа 63₁₀ является

1) 11111100
2) 111111
3) 00000101
4) 00111111

4. Какие из чисел можно сохранить в 8-разрядном беззнаковом формате?

5. При записи числа в форме A = ± m x q p , где m — это

1) порядок числа
2) основание системы счисления
3) мантисса
4) само вещественное число

6. Укажите десятичный эквивалент числа, прямой код которого 01001100 записан в 8-разрядном формате со знаком

1) 66
2) 76
3) -76
4) верного ответа в предложенных вариантах нет

7. Укажите число, записанное в естественной форме

1) 0,38005611 x 10 2
2) 1,257824E+5
3) 0,01357
4) нет числа, записанного в естественной форме

1.2.2. Представление вещественных чисел

Любое вещественное число А может быть записано в экспоненциальной форме:

Например, число 472 000 000 может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.

Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».

Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 10 9 .

Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа:

Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

Задание 6. Какие из чисел 443₈, 101010₂, 256₁₀ можно сохранить в 8-разрядном формате?

Максимальное значение в 8-разрядном формате 255 (таблица приведена в учебнике с минимальным и максимальным значением в различных разрядностях).
1) 443₈ = 4*8 2 + 4*8 1 + 3*8 0 = 4*64 + 32 + 3 = 291₁₀ Число нельзя сохранить в 8-разрядном формате.
2) 101010₂ можно сохранить в 8-разрядном формате, так как задействованы 6 разрядом из 8-ми.
3) Число 256₁₀ нельзя сохранить в данном формате.

а) 0,3800456*10 2 = 38,00456
б) 0,245*10 -3 = 0,000245
в) 1,256900Е+5 = 1,256900*10 5 = 125690
г) 9,569120Е-3 = 9,569120*10 -3 = 0,00956912

История науки и техники Com New

Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.

Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101 будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 – 1 = 255 = 11111111и минимальное 0 = 00000000. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255.

В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536 = 0000001000011000будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536 = 1000001000011000 в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 – 1 = 2 – 1 = 2 – 1 = 32767 = 111111111111111 и диапазон чисел будет находиться в пределах от -32767 до 32767.

Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.

Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:

1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;

2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);

3) к полученному обратному коду прибавить единицу к младшему разряду.

Например, для числа -536 в таком формате модуль будет равен 0000001000011000, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536, т. е. число 536, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.

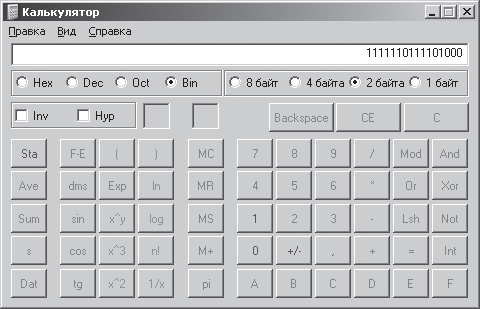
Рис. 2.6. Результат получения дополнительного кода

Необходимо помнить, что дополнительный код положительного числа – само число.

Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 – 1) … + 2 – 1 и -(2-1) … + 2 – 1.

Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).

Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.

Представление вещественного числа

Для представления вещественного числа используется как форма с ФТ, так и форма с ПТ.

Представление вещественного числа (неправильной дроби) в форме с ФТ показано на рис. 3.3. В этом случае положение разрядов числа в разрядной сетке строго фиксировано и не зависит от его значения. Следовательно, точка, отделяющая целую часть числа от его дробной части, должна занимать постоянное положение.

Рис. 3.3. Представление вещественного числа в форме с ФТ в п-разрядной сетке

Если точка фиксируется после знакового разряда сетки (перед старшим разрядом модуля), то компьютерное представление числа с ФТ имеет вид правильной дроби (рис. 3.4).

Рис. З.4. Представление правильной дроби в форме с фиксированной точкой в

Пример компьютерного представления правильной дроби в форме с ФТ показан на рис. 3.5.

Рис. 3.5. Представление дробного положительного числа 0,125ю в форме с ФТ в

однобайтовой разрядной сетке

В современных СВТ подобная форма представления используется в качестве вспомогательной, причем только для целых чисел. Существенным ее недостатком является небольшой диапазон представления чисел. Во многих прикладных задачах приходится иметь дело как с очень большими, так и очень маленькими числами, т.е. необходимо представлять числа с высокой точностью в широком диапазоне значений. Указанным требованиям отвечает форма чисел с ПТ.

Представление вещественного числа в форме с ПТ не однозначно. Для устранения этого недостатка число представляют в нормализованной форме: мантисса М для системы счисления с основанием q должна, удовлетворять условию

Для десятичной системы счисления это условие записывается как 0,1 ^ М 101 ; 0,0000101 = 0,101 • 2 -100 . Порядок также представлен в двоичной системе счисления. ?

У нормализованной формы представления числа есть одно важное преимущество: при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр, а следовательно, и максимальная точность.

Числа в форме с ПТ в компьютерах различных типов кодируются по-разному, тем не менее, существует несколько международных стандартных форматов, различающихся по точности, но имеющих единую структуру. В каждом из форматов иод мантиссу и порядок отводится строго определенное количество разрядов.

Рассмотрим следующий порядок представления числа в форме с ПТ (рис. 3.6). Старший разряд представления используется для записи знака мантиссы. За ним следует группа разрядов, определяющих порядок, а остальные разряды определяют абсолютную величину мантиссы. Размеры обеих групп разрядов фиксируются.

Рис. 3.6. Представление числа в форме с плавающей точкой

Для представления мантиссы, которая приводится к нормализованному виду, используется прямой код, а порядка числа — смещенный код, т.е. вместо истинного значения порядка хранится смещенный порядок. Основная цель использования смещенного кода — представить числа со знаком в беззнаковой форме, чтобы сохранился их порядок. В этом случае самое маленькое отрицательное число представляется последовательностью из одних нулей, самое большое число — последовательностью из одних единиц, а число 0 находится посередине, представляя собой последовательность, которая начинается единицей, после которой располагаются одни нули. Например, при использовании для хранения порядка восьми бит и значений от —128 до +127 используется смещение 128. Тогда дня представления порядка будут использоваться значения от 0 до +255, т.е. только неотрицательные числа.

Применение смещенной формы порядка позволяет выполнять операции над порядками как на;; беззнаковыми числами. Это ведет к упрощению операций сложения и вычитания порядков, а также операций сравнения нормализованных чисел.

Количество разрядов, отводимых для записи мантиссы, определяет точность представления числа. Количество разрядов, отводимых на хранение порядка, определяет диапазон значений от наименьшего отличного от 0 числа до наибольшего числа, которое можно представить в заданном формате.

Как и в случае целых чисел, в программных системах могут использоваться несколько типов данных, реализующих модель с плавающей точкой. Например, в языке Си применяются три типа данных с разной «длиной». Шестнадцатиразрядные компиляторы дня IBM-совместимых персональных компьютеров реализуют эти типы следующим образом:

• — тип Float — 4 байта, из них 23 разряда мантиссы и 8 битов порядка (числа простой точности);
• — тип Double — 8 байтов, из них 52 разряда мантиссы и 11 битов порядка (числа двойной точности);
• — тип Long double — 10 байтов, из них 65 разрядов мантиссы и 14 битов порядка.

Представление чисел в форме с ПТ приводит к усложнению алгоритмов выполнения арифметических операций, к усложнению структуры арифметичсско-логического устройства, но упрощает процесс программирования, так как значительно расширяется при этом диапазон представления чисел.