Значение двоичного кода – почему компьютеры работают с единицами и нулями

Информатика

Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).

• непозиционными (в этих системах значение цифры не зависит от ее позиции — положения в записи числа);
• позиционными (значение цифры зависит от позиции).

Непозиционные системы счисления

Позиционные системы счисления

Основание системы счисления — количество различных цифр, используемых в этой системе. Вес разряда — отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде

p_i = s i ,
где i — номер разряда, а s — основание системы счисления.

Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:

число	5	3	7	2	.	2	5
номера разрядов	3	2	1	0	-1	-2

Подсчет в двоичном формате

В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.

1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)

Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.

Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.

Основные положения

Для того чтобы разобраться что такое системы исчисления ниже приведены главные понятия, которые вам предстоит понять и запомнить. Без них вы просто не сможете двигаться дальше. Итак…

Число – абстрактная мера измерения количества чего-либо.

Цифры — знаки, с помощью которых мы представляем число.

Системой исчисления – называется совокупность правил записи чисел, с помощью набора цифровых знаков.

Теперь я попробую объяснить смысл этого определения для чайников. У вас есть набор символов – необязательно это могут быть числа, которые с помощью неких приемов и правил представляются как «цифровой код».

Алфавит (он же код) – набор знаков, используемых для записи числа.

Числовой разряд – место «позиция» знака (цифры) в числе.

После того как вы разобрались в том, что здесь написано можно перейти к следующему пункту.

Как переводить двоичные числа в десятичные

Разберемся, как быстро переводить двоичные числа в десятичные. Для примера потребуется достаточно большое двоичное число, чтобы мы не могли вычислить его на пальцах.

Запишем его в математической записи, помня, что вместо основания 10, мы используем основание 2.

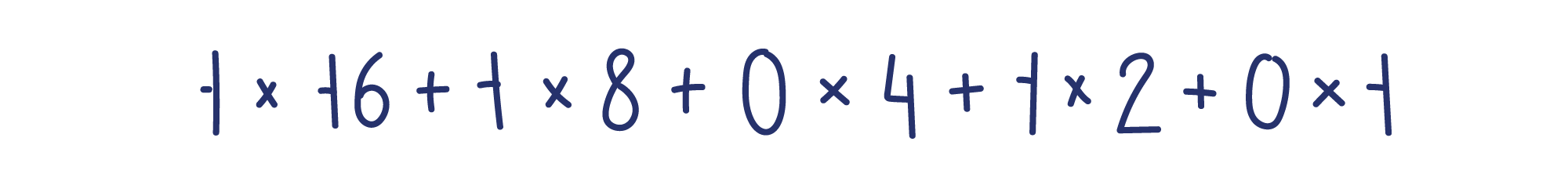
Из этого примера видно, что у всех слагаемых только два множителя — 0 и 1. Слагаемые с множителем 0 равны нулю, поэтому их можно отбросить, оставив только слагаемые с множителем 1.

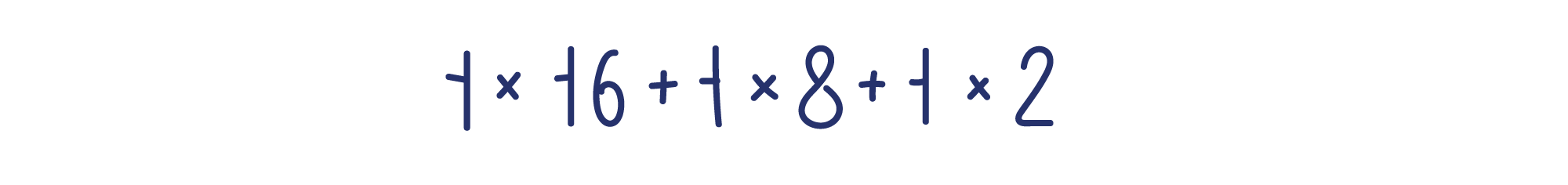
У слагаемых с множителем 1 этот множитель можно не записывать.

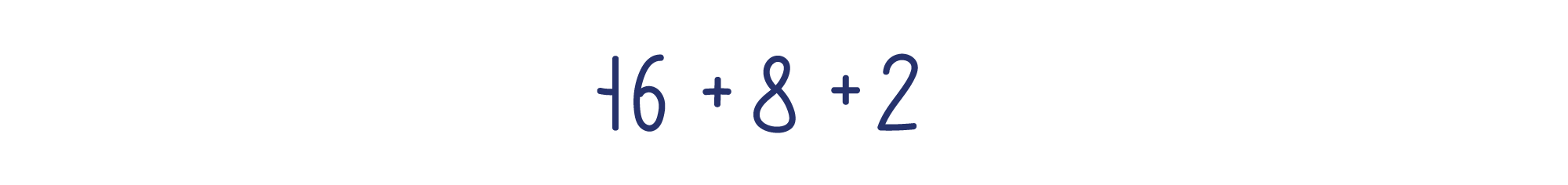
Теперь нетрудно посчитать сумму.

Вывод: число 11010 в двоичной записи — то же самое, что 26 в десятичной.

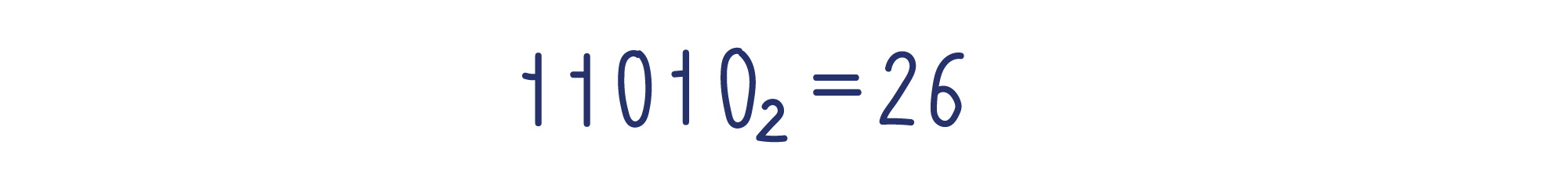
Ещё раз повторим, как перевести двоичное число в десятичное.

• Записать число в математическом виде
• Отбросить слагаемые с множителем 0
• Сложить результат

Программисты иногда запоминают некоторые степени числа два, чтобы уметь оценивать порядок двоичных чисел. Вы можете подглядывать в эту таблицу:

Двоичное число	Степень 2	Десятичное число
12	2 0	1
102	2 1	2
1002	2 2	4
10002	2 3	8
1 00002	2 4	16
10 00002	2 5	32
100 00002	2 6	64
1000 00002	2 7	128
1 0000 00002	2 8	256
10 0000 00002	2 9	512
100 0000 00002	2 10	1 024
1 0000 0000 0000 00002	2 16	65 536
1 0000 0000 0000 0000 0000 00002	2 24	16 777 216
1 0000 0000 0000 0000 0000 0000 0000 00002	2 32	4 294 967 296

С помощью этой таблицы можно переводить числа из двоичной системы в десятичную практически «в уме».

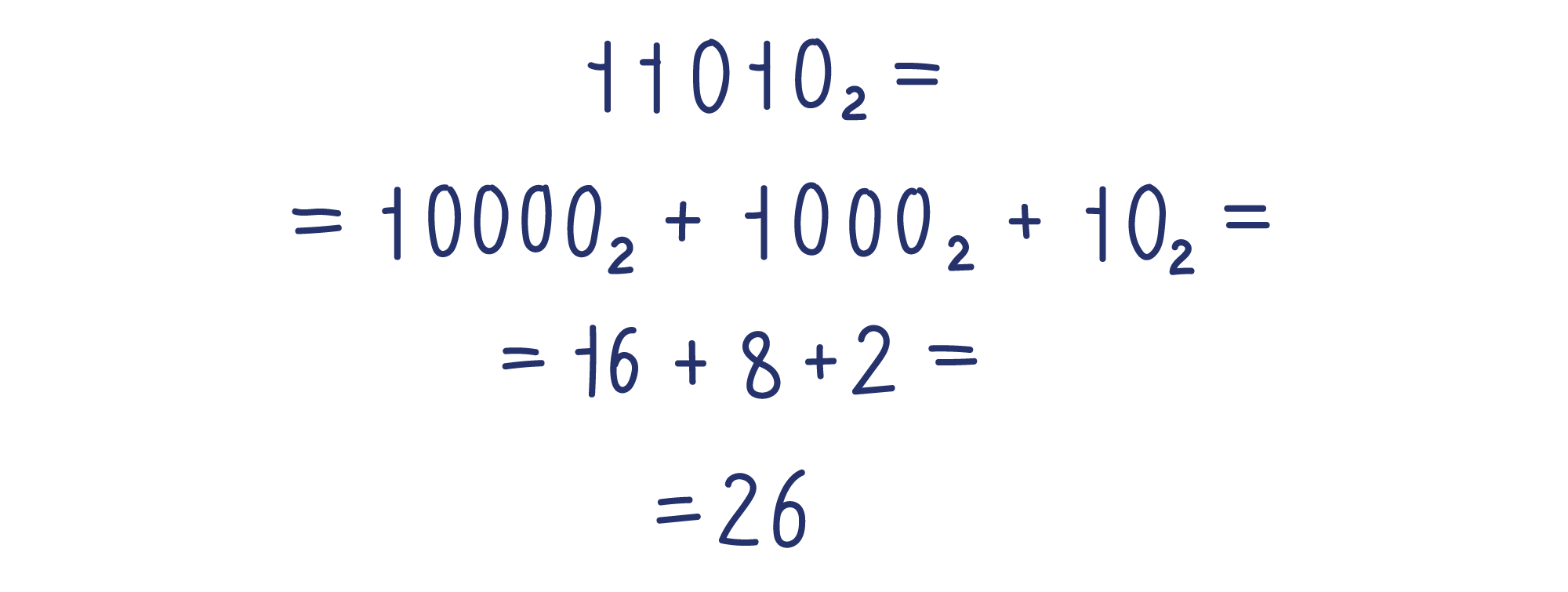
Десятичная система

Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.

Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.

Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.

Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Общие сведения

Числа записывают при помощи определенных математических символов, значение которых зависит от системы счисления (формы представления). Последней называется метод записи числа посредством определенной совокупности знаковых элементов — цифр. Не все учащиеся понимают отличие цифры от числового значения. В учебнике по информатике для 9 класса можно встретить и такое определение: системы счисления — набор символов, используемый для обозначения цифр.

Цифра — определенный математический символ, который указывает на конкретную величину. Они составляют число, а их расположение называется разрядной сеткой.

Цифры классифицируются на 2 вида: арабские и римские. Первые применяются для устного счета и представлены диапазоном от 0 до 9, который называется десятичной формой представления. Римские имеют другие обозначения. Вот расшифровка некоторых из них, которую можно перечислить в виде следующих символов: 1 — I, 2 — II, 3 — III, 4 — IV, 5 — V, 6 — VI, 7 — VII, 8 — VIII, 9 — IX, 10 — X, 40 — XL, 50 — L, 90 — XC, 100 — C, 200 — CC, 400 — CD, 500 — D.

Двоичная система счисления

Двоичная система счисления — система счисления, основанная на позиционном принципе записи чисел, в основе которой лежит база 2 Двоичная система счисления использует только два символа, цифры 0 и 1; однако, как и в любой позиционной системе, значение цифры дополнительно зависит от занимаемого ею пространства. Цифра 2 считается единицей 2-й цифры и записывается следующим образом: 10 (читать: «один, ноль»). Каждая единица следующей цифры в два раза больше предыдущей, т.е. эти единицы образуют последовательность чисел 2, 4, 8, 16, . 2n.

Для того, чтобы число, записанное в десятичной системе, было записано в D.S., оно делится на 2, а результирующие остатки 0 и 1 составляют записывается в порядке от последнего к первому: 43 = 21-2 +1; 21 = 10-2 +1; 10 = 5-2 +0; 5 = 2-2 +1; 2 = 1-2 + 0; 1 = 0-2 + 1; двоичный вход числа 43, таким образом, 101011. Таким образом, 101011 в DPS означает 1-20+1-21 + 0CH22 +1CH23 + 0-24 + 1-25.

В Д. с. с. все арифметические операции выполняются особенно легко: например, таблица умножения сводится к четности 1-1 = 1. Однако, запись в EPS очень громоздка: число 9000, например, будет иметь 14 цифр.

В связи с тем, что двоичная система счисления использует только две цифры, она часто полезна для теоретических вопросов и для вычислений на ЦВМ.

Римская система счисления

Одной из таких систем счисления является римская, которая до сих пор находит применение, например, для обозначения веков, цифр на циферблате аналоговых часов, разделов в документе и так далее. В ее основе лежат следующие числа и соответствующие им буквы латинского алфавита.

Все остальные числа получаются их комбинацией в соответствии с определенными правилами, причем 0 в римской системе отсутствует. Хотя сейчас правила довольно вольные и существует множество вариантов их трактовки отличающиеся различной степенью строгости. Мы не будем их расписывать, желающие могут найти их самостоятельно. Приведем лишь несколько примеров записи чисел в римской системе счисления.

• II — 2
• IV — 4
• XVI — 16
• XXIII — 23
• XLVIII — 48

Позиционные формы представления

Позиционные системы представления численных величин используются не только для устного счета, расчетов, но и в информационно-коммуникационных технологиях (ИКТ). Персональный компьютер переводит десятичное число в двоичную, восьмеричную и шестнадцатеричную систему (реже в троичную и пятеричную).

Основной является двоичная, поскольку из этого представления при помощи различных методик числа переводятся в другие системы исчисления. Для каждой операции существует определенный алгоритм, которого специалисты рекомендуют придерживаться.

Чтобы определить основание системы счисления, нужно внимательно рассмотреть число. Оно указывается в виде нижнего индекса или фигурными скобками. Например, А281F, 0111101100, 253. Однако в первом случае его можно не указывать, поскольку и так понятно, что это шестнадцатеричная форма записи величины (используются элементы английского алфавита).

Двоичный код можно записывать без фигурных скобок, т. к. он отличается от восьмеричной, пятеричной и других представлений чисел. Если речь идет о восьмеричной, в фигурных скобках указывается 8.

Существует также понятие мощности систем информационного исчисления. Эта характеристика показывает, какое количество данных можно закодировать. Например, картинки кодируются при помощи набора символов шестнадцатеричной формы представления, имеющей больший по сравнению с другими параметр мощности.

Работа с двоичным кодом

Двоичный код состоит из 0 и 1, что довольно просто реализовать в разнообразных электронных устройствах. Кодирование осуществляется наличием или отсутствием электромагнитного поля, закрытым или открытым переходом полупроводникового транзистора. В этом случае прослеживается связь информатики и вычислительной техники с физикой.

Для конвертации десятичной формы в двоичную применяются 2 способа. К ним относятся:

1. Деление в столбик.
2. Анализ степеней.

Новичку в сфере IT необходимо знать алгоритм конвертации двоичного кода в десятичный и обратную операцию. Методика для деления в столбик (преобразование в двоичную форму) имеет такой вид:

1. Написать десятичное представление: 117.
2. Выполнить деление на 2: 117/2=58 (1).
3. 58/2=29(0).
4. 29/2=14(1).
5. 14/2=7(0).
6. 7/2=3(1).
7. 3/2=1(1).
8. Первый разряд: 1 (остаток).
9. Результат выполнения (снизу вверх): 1110101.

Обратная конвертация из двоичного кода в десятичную форму имеет немного другую методику. Суть ее состоит в следующем:

1. Запись двоичной формы: 1110101.
2. Суммирование по разрядам (слева направо): 1+4+16+32+64=117.

Следующий способ конвертации десятичной формы в двоичную называется степенным. Суть его в том, что нужно составлять специальную таблицу:

Степень	Значение
0	1
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024

Таблица 1. Степень 2 и ее величина.

Методика преобразования строится по определенному алгоритму. Последний имеет такой вид:

1. Записать величину в десятичной форме.
2. Определить максимальное значение.
3. Написать 1 в соответствующую позицию разрядной сетки.
4. Отнять число, записанное во втором пункте, от первоначального значения.
5. Выполнить все действия во 2, 3 и 4 пунктах в строгой последовательности.
6. Записать окончательный результат.

Чтобы понять методику конвертации при помощи степенного способа, нужно разобрать ее реализацию на практическом примере:

1. Десятичная форма: 117.
2. Максимум: по таблице 1 — 2^6 (запись 1).
3. Разность: 117-2^6=53.
4. MAX: 2^5=32 (1).
5. 53-32=21.
6. MAX: 2^4 (1).
7. 21-16=5.
8. MAX: 2^2=4 (1).
9. MAX: 2^0 (1).
10. Результат: 1110101.

Каждый ученик должен сам выбрать для себя оптимальный способ. Для проверки можно воспользоваться специальным калькулятором или веб-приложением для конвертации из одной системы представления величины в другую.

Восьмеричная запись

Перевод в восьмеричную форму из десятичной осуществляется через двоичный код. После чего элементы разрядной сетки группируются по триадам, а затем высчитывается результат. Чтобы привести число к восьмеричной форме, нужно использовать следующий алгоритм:

1. Написать искомое число.
2. Перевести в двоичный код одним из способов.
3. Сгруппировать по 3 разряда.
4. Расписать каждую группу, присваивая ей определенную величину.
5. Записать искомое значение.

Для использования алгоритма необходимо разобрать пример преобразования числа 117 в восьмеричный код. Это делается таким образом:

1. Искомое значение: 117.
2. Двоичный код: 1110101.
3. Группировка (если не хватает разрядов, нужно дописать нули): .
4. Результат: 165.

Алгоритм обратного преобразования строится на конвертации сначала в двоичную, а затем в десятичную форму. Он имеет следующий вид:

1. Написать число: 165.
2. Разбить по разрядам: .
3. Перевести в двоичное представление: =1110101.
4. Перевод в десятичную: 117.

Конвертация проверяется при помощи различных онлайн-сервисов или калькулятора. Восьмеричная система позиционного счисления обладает большей мощностью, чем двоичная.

Шестнадцатеричный формат

Для выполнения перевода десятичного числа в шестнадцатеричное (ее также можно назвать HEX-представление) существует определенная методика, похожая на предыдущую (восьмеричную), но имеющая некоторые отличия. Последние заключаются в выделении тетрад (4 элемента), а также расширения количества математических символов (от 0 до 9, А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15). Алгоритм имеет следующий вид:

1. Перевести десятичную форму в двоичную.
2. Сгруппировать разряды по 4 элемента. Если в какой-то группе не хватает цифр, нужно дописать нули.
3. Написать числа для каждой группы.
4. Записать окончательный результат.

Для полного понимания методики конвертации нужно разобрать практический пример. Реализация алгоритма выглядит следующим образом:

1. Записать число: 117.
2. Написать двоичную форму: 1110101.
3. Образовать тетрады: .
4. Значения для каждой группы: 11=В и 5=5.
5. Результат: В5.

Обратная методика преобразования строится на переводе в двоичную форму, а затем в десятичную. Она имеет такой вид:

1. Записать шестнадцатеричную величину: В5.
2. Расписать каждый элемент: В=0111 и 5=0101.
3. Перевод в десятичную систему: 117.

Во втором пункте специалисты рекомендуют указывать основание, т. к. этот прием поможет избежать ошибок при конвертации. Кроме того, результат необходимо проверять при помощи веб-сервиса или специального калькулятора.

Таким образом, системы счисления используются для конвертации цифровой информации в машинный код для дальнейшей обработки и выдачи готовых результатов, полученных во время вычислительного процесса.