Числа в памяти компьютера
презентация к уроку по информатике и икт (8 класс)
Цель: Дать представление целых и вещественных чисел в памяти компьютера; Выяснить как диапазон значений чисел зависит от размера ячейки; Узнать о переполнении.
Цифровые технологии Вся информации в памяти компьютера хранится в двоичном виде. Числовая информация Целые числа Вещественные числа
Представление целых чисел Положительные Хранятся в компьютере в прямом коде Отрицательные Хранятся в компьютере в дополнительном коде
Ячейка Часть памяти, в которой хранится число, называется ячейкой. Минимальный размер ячейки – 8 бит или 1 байт.
Прямой код 33 10 =100001 2 33 10 = 00 100001 2 = > 00100001 представление целого положительного числа 33 в двоичном виде.
Отрицательное число -33 10 Прямой код модуля числа 00100001 Обратный код (инверсия прямого кода) 11011110 Дополнительный код (+1) 11011111 = > 11011111 представление целого отрицательного числа -33 в двоичном виде.
Знак числа Самый старший разряд хранит знак числа. 0 0100001 1 1011111 Число положительное Число отрицательное
Диапазон значений Диапазон значений зависит от разрядности ячейки Для 8-разрядной ячейки Минимальное число 10000000 2 =-128 10 Максимальное число 01111111 2 =127 10 -128 ≤x≤ 127 или -2 7 ≤х≤ 2 7 -1
Диапазон значений Для 16-разрядной ячейки -32 768 ≤x≤ 32 767 или -2 15 ≤х≤ 2 15 -1 Для 32-разрядной ячейки -2 147 483 648 ≤x≤ 2 147 483 647 или -2 31 ≤х≤ 2 31 -1
Переполнение Выход результатов вычислений за границы допустимого диапазона, следовательно результат вычислений неправильный. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора.
Представление вещественных чисел Всякое вещественное число можно записать в виде: X=m*p n , где m — мантисса, p – основание, n – порядок. Пример: 32,344=0,32344*10 2
Хранение вещественных чисел 32-разрядная ячейка – представление с одинарной точностью, 64-разрядная ячейка – представление с двойной точностью Порядок (8 разрядов) Мантисса (24 разряда)
Особенности работы компьютера с вещественными числами Диапазон вещественных чисел ограничен. Но он значительно шире, чем для представления целых чисел. Для 32-разрядной ячейки: -3,4*10 38 ≤х≤ 3,4*10 38
Особенности работы компьютера с вещественными числами Выход за диапазон (переполнение) – аварийная ситуация для процессора, который прерывает свою работу. Результаты машинных вычислений с вещественными числами содержат погрешность. При использовании двойной точности эта погрешность уменьшается.
Задание Записать внутреннее представление десятичных чисел: 42, — 42
Домашнее задание Пар 19, стр. 136 № 3 Просмотр видео урока : https://www.youtube.com/watch?v=ZRJAf885kVQ
2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
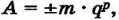
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 000 000 может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 10 9 .
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 10 1111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
2. Представление вещественных чисел
В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.
Попробуйте обосновать это утверждение.
Вещественные числа записываются в естественной или в экспоненциальной форме.
В жизни мы чаще пользуемся естественной формой записи чисел, при которой: число представляется последовательностью десятичных цифр со знаком плюс или минус, знак плюс может опускаться, для разделения целой и дробной частей числа используется запятая.
Например: 12,34; 0,0056; -708,9.
В экспоненциальной форме вещественное число а представляется как а = ± m • q p , где m — мантисса числа, q — основание системы счисления, р — порядок числа.
Например, длину некоторого отрезка, равного 47,8 см, можно записать так:
1) 478 • 10 -1 см;
2) 47,8 • 10 0 см;
3) 4,78 • 10 1 см;
4) 0,478 • 10 2 см;
5) 0,000478 • 10 5 см.
Такое многообразие вариантов записи в экспоненциальной форме одного и того же числа не всегда удобно. Для однозначного представления вещественных чисел в компьютере используется нормализованная форма.
Нормализованная запись отличного от нуля вещественного числа 1) — это запись вида а = ± m • q p , где р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ? m < q.
1) Стандарт IEEE 754.
Примеры нормализации чисел:
1) 31,415926 = 3,1415926 • 10 1 ;
2) 1000 = 1,0 • 10 3 ;
3) 0,123456789 = 1,23456789 • 10 -1 ;
4) 0,00001078 = 1,078 • 108 -5 ;
5) 1000,00012 = 1,00000012 • 102 11 ;
6) AB,CDEF16 = A,BCDEF16 • 1016 1 .
Диапазон вещественных чисел в памяти компьютера очень широк, но, тем не менее, ограничен. Множество вещественных чисел, которые могут быть представлены в компьютере, конечно.

Поясним это на примере калькулятора, который производит вычисления в десятичной системе счисления. Пусть это будет калькулятор с десятью знакоместами на дисплее:
• 6 знакомест отводится под мантиссу (одно знакоместо отводится под знак мантиссы, четыре — под цифры мантиссы, одно — под точку, разделяющую целую и дробную части мантиссы);
• одно знакоместо отводится под символ «Е»;
• три знакоместа отводятся под порядок (одно — под знак порядка, два — под цифры порядка).
У калькуляторов первая значащая цифра, с которой и начинается мантисса, изображается перед точкой.
Число 12,34 в таком калькуляторе будет представлено как +1.234Е+01.
Число 12,35 будет представлено как + 1.235Е+01.
Как известно, между числами 12,34 и 12,35 находится бесконечное множество вещественных чисел, например: 12,341; 12,3412; 12,34123 и т. д.
Каждое из этих чисел в нашем калькуляторе будет представлено как + 1.234Е+01. Для последних разрядов у нас просто не хватает знакомест! Аналогичная ситуация имеет место и в компьютерном представлении вещественных чисел, независимо от того, ячейки какой разрядности там использованы.
Получается, что точно мы можем представить в компьютере лишь некоторую конечную часть множества вещественных чисел, а остальные числа — лишь приближённо.
Таким образом, множество вещественных чисел, представляемых в компьютере, дискретно, конечно и ограничено.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 6310 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме:
а) 0,3800456 • 10 2 ;
б) 0,245 • 10 -3 ;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Преобразования чисел
Преобразования чисел В случае встроенных числовых типов (sbyte, int, float и т.д.) явное преобразование требуется тогда, когда вы пытаетесь сохранить большее значение в меньшем контейнере, поскольку при этом может происходить потеря данных. По сути, это способ сказать
СОРТИРОВКА ЧИСЕЛ Одним из наиболее распространенных тестов для машин является сортировка. Мы хотим разработать программу для сортировки целых чисел. Снова применим принцип черного ящика и подумаем в терминах ввода и вывода. Наш общий замысел, показанный на рис. 10.4,
Алгоритм представления в компьютере беззнаковых целых чисел
Беззнаковое целое положительное число перевести в двоичную систему счисления.
Записать число в $8$ разрядах так, чтобы младший разряд числа соответствовал младшему разряду ячейки.
Дополнить число, если необходимо, слева нулями до нужного числа разрядов ($8$-ми, $16$-ти, $32$-х).
Получить 8-разрядное представление числа $30$.
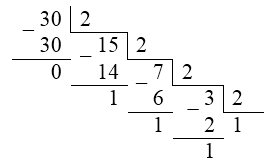
Дополним до $8$-ми разрядов:
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.



Двойная точность
Поскольку все вычисления были расписаны и объяснены в предыдущем пункте, здесь мы расскажем всё очень коротко. Для чисел с двойной точностью обычно выделяется 11 разрядов для порядка и его знака, а также 53 разряда для мантиссы.
П = 1111111111 2 = 1023 10 .
М = 2 52 -1 = 2 (10*5.2) = 1000 5.2 = 10 15.6 . Округляем в большую сторону и получаем максимальное число Х = 2 1023 с точностью до «м».
Надеемся, информация про представление целых и вещественных чисел в компьютере, которую мы предоставили, пригодится вам в обучении и будет хоть немного понятнее, чем то, что обычно пишут в учебниках.












