Кодирование информации
Ежедневно человек сталкивается с кодированием информации. Огромное количество данных из окружающего мира поступает к нему в форме разнообразных сигналов, звуков, вкусовых и тактильных ощущений. Вместе оно составляет своеобразный код, совокупность условных обозначений. Кодирование информации – это преобразование исходных данных с помощью определенного алгоритма.
План урока:
Примеры кодирования информации:
- трансляция письменных сообщений с использованием русских букв (АБВГД…ЭЮЯ);
- запись чисел цифрами (0123456789);
- использование языка жестов при общении глухонемых людей
Другими словами, переход сообщения из одной формы ее в другую, согласно определенным правилам, и выражает в чем суть кодирования информации.
Информация проходит кодирование в целях:
- упрощения сбора исходных данных;
- сокращения объема занимаемой памяти информационными сообщениями;
- удобства хранения материалов;
- эффективной обработки и обмена информацией;
- сокрытия необходимых сведений.
История кодирования информации насчитывает сотни веков. Издавна люди использовали криптограммы (зашифрованные сообщения).
В 19 веке с изобретением телеграфа С. Морзе был придуман и принципиально новый способ шифрования. Телеграфное сообщение передавалось по проводам последовательностью коротких и долгих сигналов (точка и тире).
Вслед за ним Ж. Бодо создал основополагающий в истории современной информатики метод бинарного кодирования информации, который заключается в применении всего двух различающихся электрических сигналов. Кодирование информации в компьютере также подразумевает использование двух чисел.
Разработанная в 1948г. К. Шенноном «Теория информации и кодирования» стала основополагающей в современном кодировании данных.
Кодирование информации в информатике, одна из базовых тем. Понимание для чего нужна процедура кодирования передаваемой информации, каким образом она осуществляется, поможет в изучении принципов работы компьютера.
Контрольные вопросы
1. Приведите примеры знаковых систем. Какой может быть физическая природа знаков?
2. В чем состоит различие между естественными и формальными языками?
3. Обладают ли генетическим кодом растения? Животные? Человек?
4. Почему в компьютерах используется двоичная знаковая система для кодирования информации?
Перевод чисел из десятичной системы счисления в другие позиционные системы счисления
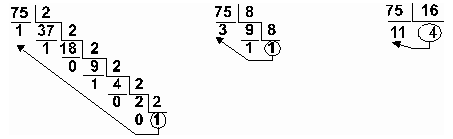
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
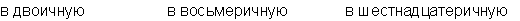
Укажите основные виды кодирования текстовой информации?
Укажите основные виды кодирования текстовой информации.
А) графический Б) символьный В) знаковый Г) числовой.

1.1.3. Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1,2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
Например: 10638 = 1 • 8 3 + 0 • 8 2 + 6 • 8 1 + 3 • 8 0 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.

Звуки и их разрядность
Человек воспринимает звуковые волны (колебания воздуха) с помощью слуха в форме звука различных громкости и тона. Чем больше интенсивность звуковой волны, тем громче звук, чем больше частота волны, тем выше тон звука. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму с помощью временной дискретизации. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, для каждого такого участка устанавливается определенная величина интенсивности звука.
В каждом современном компьютере предусмотрена звуковая плата, колонки, микрофон. С их помощью производится запись, сохраняются и воспроизводятся звуки — волны с определённой частотой и амплитудой. Программное обеспечение для компьютеров преобразовывает звуковые сигналы в последовательность нулей и единиц. Для этого использунтся аудиоадаптер или звуковая плата. Устройство подключается к компьютеру с целью преобразования электроколебаний звуковой частоты в двоичный код. Процесс преобразования выполняется как при вводе звуков в компьютер так и при обратном их преобразовании.
Для человека звук тем громче, чем больше амплитуда сигнала, и тем выше тон, чем больше частота сигнала. Компьютер — устройство цифровое, поэтому непрерывный звуковой сигнал должен быть преобразован в последовательность электрических импульсов (нулей и единиц). Оцифровку звука выполняет специальное устройство на звуковой плате. Называется оно аналого-цифровой преобразователь (АЦП). Обратный процесс — воспроизведение закодированного звука производится с помощью цифро-аналогового преобразователя (ЦАП).
В процессе кодирования непрерывного звукового сигнала производится его дискретизация по времени, или, как говорят, «временная дискретизация».
Для записи аналогового звука и г го преобразования в цифровую форму используется микрофон, подключенный к звуковой плате. Качество полученного цифрового звука зависит от количества измерений уровня громкости звука в единицу времени, т. е. частоты дискретизации. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее «лесенка» цифрового звукового сигнала повторяет кривую аналогового звукового сигнала.
Глубина кодирования звука — это количество бит, используемое для кодирования различных уровней сигнала или состояний. Современные звуковые карты обеспечивают 16-битную глубину кодирования звука, и тогда общее количество различных уровней громкомти, который сможет распознать компьютер будет: N = 2 16 = 65536.
Частота дискретизации- это количество измерений уровня звукового сигнала в единицу времени. Эта характеристика показывает качество и точность процедуры двоичного кодирования. Измеряется в герцах (Гц).
Одно измерение за одну секунду соответствует частоте 1 Гц, 1000 измерений за одну секунду — 1 килогерц (кГц). Частота дискретизации звукового сигнала может принимать значения от 8 до 196 кГц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц — качеству звучания аудио-CD. Достаточно высокое качество звучания достигается при частоте дискретизации 44 кГц и глубины кодирования звука, равной 16 бит.
Оцифрованный сигнал в виде набора последовательных значений амплитуды уже можно сохранить в памяти компьютера. В случае, когда записываются абсолютные значения амплитуды, такой формат записи называется PCM ( Pulse Code Modulation). Стандартный аудио компакт-диск (CD-DA), применяющийся с начала 80-х годов 20-го столетия, хранит информацию в формате PCM с частотой дискретизации 44.1 кГц и разрядностью квантования 16 бит.
Подробнее о свойствах звука можно прочитать в статье Звук
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.



Применение восьмеричной и шестнадцатеричной систем счисления
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре(шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой натриады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
10. Верны ли следующие равенства? а) 334 = 217;
б) 338 = 214.
11. Найдите основание х системы счисления, если: а) 14х = 910;
б) 2002х = 13010.
19. Вычислите выражения: а) (11111012 + AF16) : 368; б) 1258 + 1012 ? 2A16 ? 1418. Ответ дайте в десятичной системе счисления.












