Учитель информатики

Урок 3. Как работает компьютер

Для успешного «общения» с компьютером вредно воспринимать его как черный ящик, который вот-вот выдаст что-то неожиданное. Чтобы понимать реакцию компьютера на Ваши действия, нужно знать как он устроен и как работает.

В этом IT-уроке узнаем, как работает большинство вычислительных устройств (к которым относятся не только персональные компьютеры).

Во втором уроке мы разобрались, что компьютер нужен для обработки информации, её хранения и передачи. Посмотрим же, как происходит обработка информации.

1.1.1. Общие сведения о системах счисления

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.

В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.

Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.

Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления

Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:

• 1) унарная система;
• 2) непозиционные системы;
• 3) позиционные системы.

Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.

Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:

Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа.Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Сложности реализации

Если обобщить, то есть множество физических явлений, имеющих два устойчивых состояния и на этих явлениях базируются различные разработки — те же реле, магнитная запись и многое другое. Если мы будем использовать некие дополнительные значения кроме нуля и единицы, мы неизбежно столкнёмся с широким рядом сложностей. Например, физическое затухание сигнала при передаче данных по кабелю или по радиоканалу. При бинарной логике мы принимаем в каждый момент времени либо логическую единицу, то есть, наличие сигнала, либо логический ноль, то есть, его отсутствие. Предположим, мы решили предавать троичный сигнал. В этом случае ноль — это отсутствие сигнала, единица — это наличие сигнала, а третье значение — это сигнал половинной мощности. В идеальном мире это работало бы хорошо, в реальном мире любой провод так или иначе служит антенной, на которую воздействуют электромагнитные волны различной частоты, существуют перепады напряжения в источниках питания, а радиоэфир на некоторых частотах — это просто кошмар. Тот же вайфай, работающий на частоте 2.4 гигагерца в многоквартирных домах напоминает арену, на которой за полосу пропускания борется несколько десятков устройств, многие из которых в зависимости от канала так или иначе влияют на работу друг друга. То есть, уровень сигнала может плавать, а может и резко меняться под воздействием внешних факторов. Например, включенной кем-то микроволновки. Конечно, всё это решаемо на уровне алгоритмов обработки ошибок, но сложность реализации в результате неизбежно будет повышаться.

То есть, для того, чтобы создать компьютер, использующий троичную логику, необходимо выполнить несколько условий: Во-первых, создать процессор, обрабатывающий данные в троичной системе счисления, то есть, найти замену транзистору, которая сможет принимать три устойчивых состояния. Во-вторых, желательно найти некий энергонезависимый носитель информации, который для каждой своей ячейки хранения мог бы принимать три устойчивых состояния. Можно обойтись и существующими, но использоваться они будут неэффективно. В-третьих, разработать алгоритмы обработки и передачи данных, базирующихся на троичной системе.

Арифметические основы ЭВМ

Представление числовой информации в компьютере

В компьютерах используются три вида чисел: с фиксированной точкой (запятой), с плавающей точкой (запятой) и двоично-десятичное представление. Точка (запятая) — это подразумеваемая граница целой и дробной частей числа, разряды и формулы (4.1).

Все современные компьютеры имеют центральный процессор или центральное процессорное устройство — CPU ( Central Processing Unit ), предназначенное для обработки чисел с фиксированной точкой. Одной из важнейших его характеристик является разрядность — количество двоичных разрядов, представляющих значение числа. Основным достоинством CPU служит простота алгоритмов выполнения операций и, соответственно, высокая скорость операций.

У чисел с фиксированной точкой в двоичном формате предполагается строго определенное место точки (запятой). Обычно это место определяется или перед первой цифрой числа, или после последней цифры числа. Если точка фиксируется перед первой значащей цифрой, то это означает, что число по модулю меньше единицы. Диапазон изменения значений чисел определяется неравенством:

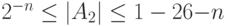
Если точка фиксируется после последней цифры, то это означает, что -разрядные двоичные числа являются целыми. Диапазон изменения их значений составляет:

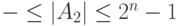
Перед самым старшим из возможных цифровых разрядов двоичного числа фиксируется его знак. Положительные числа имеют нулевое значение знакового разряда, отрицательные — единичные. Каждая цифра двоичного числа » /> занимает один бит соответствующего -разрядного формата.

Существенным недостатком представления чисел с фиксированной точкой служит тот факт, что аппроксимация малых чисел связана с большой относительной ошибкой. Для чисел же, приближающихся по величине к максимально возможным (), относительная ошибка уменьшается. Абсолютная же ошибка представления чисел с фиксированной точкой всегда лежит в одних и тех же пределах независимо от величины чисел.

Другой формой представления чисел является представление их в виде чисел с плавающей точкой (запятой). Представление чисел с плавающей точкой необходимо использовать, когда обрабатываемые числа имеют очень большой диапазон изменения. Эта ситуация типична для научно-технических расчетов (тригонометрические, экспоненты, логарифмы). Поэтому все современные микропроцессоры в качестве дополнения к CPU имеют математические сопроцессоры . Их обычно называют блоками или устройствами с плавающей точкой — FPU ( Floating Point Unit), или числовым расширением процессора — NPX ( Numeric Processor eXtension). Сочетание параллельно работающих CPU и FPU позволяет добиться большей скорости и большей точности вычислений.

Числа с плавающей точкой представляются в виде мантиссы и порядка , иногда это представление называют полулогарифмической формой числа. Например, число =373″ /> можно представить в виде , при этом , основание системы счисления подразумевается фиксированным и равным десяти. Для двоичных чисел в этом представлении также формируется и порядок при основании системы счисления, равном двум.

что соответствует записи

Таблица 14.2. Правила сложения двоичных цифр Значения двоичных чисел А и В Разряд суммы Перенос в следующий разряд 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1

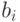
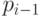
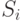
Здесь показаны правила сложения двоичных цифр , одноименных разрядов с учетом возможных переносов из предыдущего разряда » />.

Подобные таблицы можно было бы построить для любой другой арифметической и логической операции (вычитание, умножение и т.д.), но именно данные этой таблицы положены в основу выполнения любой операции ЭВМ. Под знак чисел отводится специальный знаковый разряд. Знак «+» кодируется двоичным нулем, а знак «-» — единицей. Действия над прямыми кодами двоичных чисел при выполнении операций создают большие трудности, связанные с необходимостью учета значений знаковых разрядов:

• во-первых, следует отдельно обрабатывать значащие разряды чисел и разряды знака;
• во-вторых, значение разряда знака влияет на алгоритм выполнения операции, например, сложение может заменяться вычитанием и наоборот.

Во всех ЭВМ без исключения все операции выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и цифровые разряды, а также заменять операцию вычитания операцией сложения.

Различают прямой код (П), обратный код (ОК) и дополнительный код (ДК) двоичных чисел.

Унарная система счисления: что это

Непозиционная система счисления — это практически не применяемая в информатике СС. В ней значение числа определяется как функция от величин стоящих рядом символов, исходя из правил. Яркий пример унарной системы счисления – римская, которая применяется разве для обозначения столетий. Она основана на десятке букв латинского алфавита, основная из которых – I (английская) – единица.

Изначально для записи количества предметов ставилось столько единиц (I), сколько было объектов, что неудобно – число «палочек» приходилось каждый раз подсчитывать. Чуть упростило задачу введение иных символов, при записи огромных значений система также оказалась неудобной из-за громоздкости записи и ряда правил для вычисления значений.

Правила записи чисел римлянами:

• Меньшая цифра добавляется до большей, если идёт после неё.
• Если меньшая предшествует старшей – отнимается.
• Две меньших цифры рядом, если следуют перед большей, не ставятся.
• D, V, L используют в числе лишь раз.
• I, X. C, M – применяются до трёх раз.

Кроме сложности записи, восприятия информации, совершения математических операций СС не прижилась по причине простоты фальсификации. Если в десятичной более или менее незаметно можно исправить 3 на 8 и добавить единицу в конце или начале, заниматься фальсификациями с римскими цифрами намного проще. Потому от неё отказались.

В цифровой технике унарные СС не применяются по названным причинам.

Шестнадцатеричная система счисления

Мы знаем, что компьютер использует числа для представления любой информации. Например, цвета хранятся в виде трёх чисел — яркости красной, зелёной и синей компонентов цвета. На каждый компонент отводится восемь двоичных позиций, поэтому максимальная яркость компонента равна 11111111₂ или 255. Цвет целиком описывается большим 24-х разрядным двоичным числом, например, 11111010 10000000 01110010. Это цвет Salmon из таблицы цветов HTML, он же лососевый цвет.

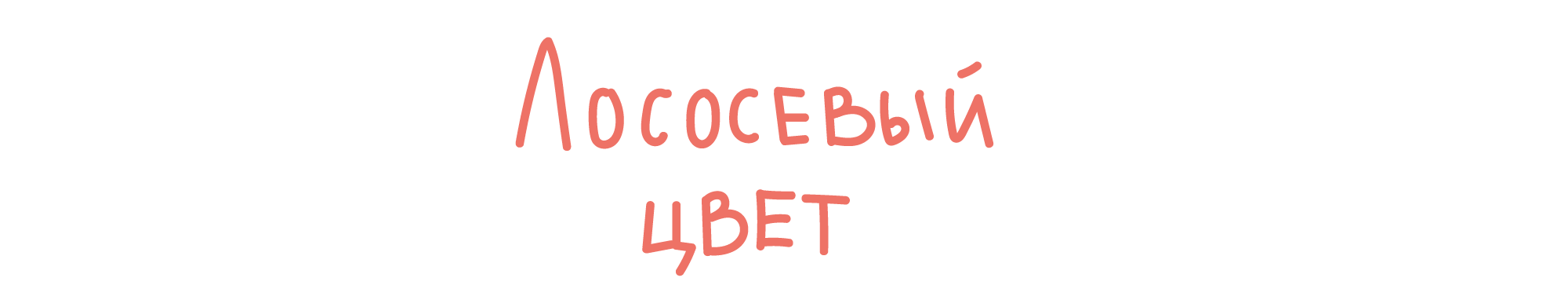
Старшие восемь позиций отводятся для хранения красного компонента, средние восемь — зелёного, и младшие восемь — синего. Мы видим, что такая запись очень громоздка и неудобна.

Кажется, что цвет удобнее записать как десятичное число 16416882. Хотя оно занимает меньше места, по нему трудно понять, какова яркость каждого компонента.

Чтобы записывать большие двоичные числа, программисты придумали использовать шестнадцатеричную систему счисления:

• В десятичной системе десять цифр, а в шестнадцатеричной — шестнадцать
• В десятичной системе соседние позиции отличаются в десять раз, а в шестнадцатеричной — в шестнадцать раз

Как и в случае с двоичной системой, цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 заимствуются из десятичной системы. Но в данном случае этих цифр не хватает: нужно ещё шесть. Их в шестнадцатеричной системе принято обозначать первыми буквами английского алфавита:

Основание 16	Основание 10	Основание 2
0	0	0
1	1	1
2	2	10
3	3	11
4	4	100
5	5	101
6	6	110
7	7	111
8	8	1000
9	9	1001
A	10	1010
B	11	1011
C	12	1100
D	13	1101
E	14	1110
F	15	1111

Шестнадцатеричная система счисления хороша тем, что группа из четырёх двоичных цифр кодируется одной шестнадцатеричной цифрой. Таким образом, лососевый цвет выглядит как:

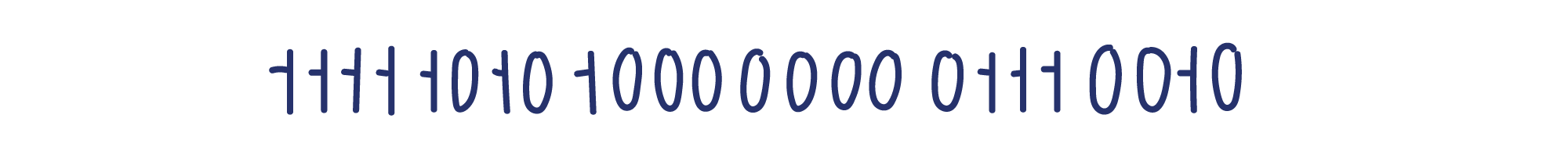
В шестнадцатеричной системе счисления он записывается так:

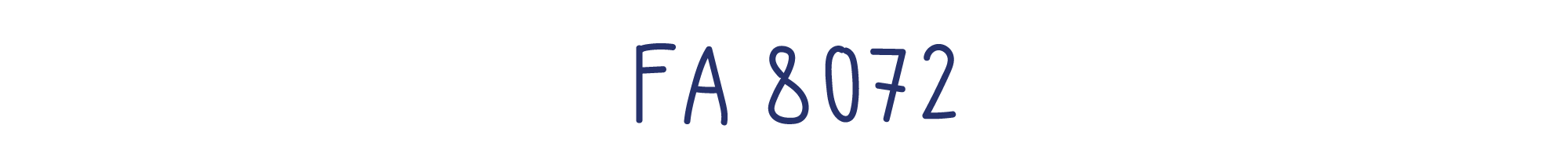
Вначале трудно понять, каков порядок у шестнадцатеричного числа FA. Как и в случае с двоичными числами, программисты обычно помнят порядки круглых шестнадцатеричных чисел. Но можно не запоминать, а подглядывать в эту таблицу:

Шестнадцатеричное число	Десятичное число
1016	16
2016	32
3016	48
4016	64
5016	80
6016	96
7016	112
8016	128
9016	144
A016	160
B016	176
C016	192
D016	208
E016	224
F016	240
10016	256
100016	4 096
1 000016	65 536
10 000016	1 048 576
100 000016	16 777 216
1000 000016	268 435 456
1 0000 000016	4 294 967 296

Чтобы переводить числа из десятичной системы в шестнадцатеричную и обратно, двоичное представление можно использовать как промежуточное. Часто это самый простой способ: двоичное и шестнадцатеричное представления без труда переводятся друг в друга.

Представление числовой информации. Сложение и умножение в разных системах счисления

Представление числовой информации с помощью систем счисления

Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.

Система счисления — это система записи чисел с помощью определенного набора цифр.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.

Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.

Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.

Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.

Например: 8527 = 8 ⋅ 10 3 + 5 ⋅ 10 2 + 2 ⋅ 10 1 + 7 ⋅ 10 0 .

Развернутая форма записи чисел произвольной системы счисления имеет вид

$a$ — цифры численной записи, соответствующие разрядам;

$m$ — количество разрядов числа дробной части;

$n$ — количество разрядов числа целой части;

$q$ — основание системы счисления.

Например, запишем развернутую форму десятичного числа $327.46$:

Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.

Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В₁₂ можно расписать так:

7А,5В₁₂ = В ⋅ 12 -2 + 5 ⋅ 2 -1 + А ⋅ 12 0 + 7 ⋅ 12 1 .

В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.

Перевод чисел в позиционных системах счисления

Перевод чисел из произвольной системы счисления в десятичную

Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂ = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 13₁₀;

17D,ECH = 12 ⋅ 16 –2 + 14 ⋅ 16 –1 + 13 ⋅ 160 + 7 ⋅ 16 1 + 1 ⋅ 16 2 = 381,921875.

Перевод чисел из десятичной системы счисления в заданную

Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:

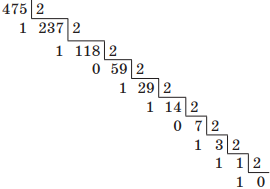
Читая остатки от деления снизу вверх, получим 111011011.

1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 475₁₀.

Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например, переведем десятичную дробь 0,375₁₀ в двоичную систему счисления:

Полученный результат — 0,011₂.

Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2 І ; І = 3).

Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

1234,777₈ = 001 010 011 100,111 111 111₂ = 1 010 011 100,111 111 111₂;

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂.

При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2 І ; І = 4).

Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.

Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.

1234,AB77₁₆ = 0001 0010 0011 0100,1010 1011 0111 0111₂ = 1 0010 0011 0100,1010 1011 0111 0111₂;

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂.

При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.

Например, переведем троичное число 211₃ в семеричную систему счисления. Для этого сначала преобразуем число 211₃ в десятичное, записав его развернутую форму:

211₃ = 2 ⋅ 3 2 + 1 ⋅ 3 1 + 1 ⋅ 3 0 = 18 + 3 + 1 = 22₁₀.

Затем переведем десятичное число 22₁₀ в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:

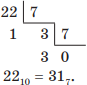
Примеры решения задач

Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.

Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 12₁₀ = 110_n = 0 ·n 0 + 1 · n 1 + 1 · n 2 . Составим уравнение: n 2 + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 110₃ = 0· 3 0 + 1 · 3 1 + 1 · 3 2 = 0 + 3 + 9 = 12 .

Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.

Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 22₁₀ = 34₆ = 24₉ = 14₁₈.

Ответ: 6, 9, 18.

Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.

Решение. Для удобства воспользуемся восьмеричной системой счисления. 101₂ = 5₈. Тогда число х можно представить как x = 5 · 8 0 + a₁ · 8 1 + a₂ · 8 2 + a₃ · 8 3 + . , где a₁, a₂, a₃, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 8 2 > 25), т. е. такие числа должны иметь представление x = 5 + a₁ · 8. Поскольку x ≤ 25 , допустимыми значениями a₁ будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:

a₁ = 0; x = 5 + 0 · 8 = 5;.

a₁=1; x = 5 + 1 · 8 = 13;.

a₁ = 2; x = 5 + 2 · 8 = 21;.

Ответ: 5, 13, 21.

Арифметические операции в позиционных системах счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0 ⋅ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ⋅ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ⋅ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ⋅ 1 = 1

Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.

Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:

Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:

Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:

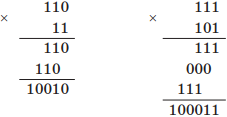
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.

Например, выполним сложение восьмеричных чисел 36₈ и 15₈, а также вычитание шестнадцатеричных чисел 9С₁₆ и 67₁₆:

При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.

Представление чисел в компьютере

Формат с фиксированной запятой

В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно

1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для п-разрядного представления диапазон будет составлять от 0 до 2 n – 1.

Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.

Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2 n − |А|.

Алгоритм получения дополнительного кода отрицательного числа:

1. Записать прямой код числа в п двоичных разрядах.

2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)

3. Прибавить единицу к полученному обратному коду.

Например, получим дополнительный код числа –2014₁₀ для шестнадцатиразрядного представления:

Прямой код	Двоичный код числа 201410 со знаковым разрядом	1000011111011110
Обратный код	Инвертирование (исключая знаковый разряд)	1111100000100001
Прибавление единицы	1111100000100001 + 0000000000000001
Дополнительный код	1111100000100010

При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.

1) Найдем разность 13₁₀ – 12₁₀ для восьмибитного представления. Представим заданные числа в двоичной системе счисления:

Запишем прямой, обратный и дополнительный коды для числа –12₁₀ и прямой код для числа 13₁₀ в восьми битах:

1310	–1210
Прямой код	00001101	10001100
Обратный код	—	11110011
Дополнительный код	—	11110100

Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):

Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.

2) Найдем разность 8₁₀ – 13₁₀ для восьмибитного представления.

Запишем прямой, обратный и дополнительный коды для числа –13₁₀ и прямой код для числа 8₁₀ в восьми битах:

810	–1310
Прямой код	00001000	10001101
Обратный код	—	11110010
Дополнительный код	—	11110011

Вычитание заменим сложением:

В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:

11111011 – 00000001 = 11111010.

Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –5₁₀.

Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2 n–1 , а максимальное: |А| = 2 n–1 или А = –2 n–1 – 1.

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно

А = –2 31 = –2147483648₁₀.

Максимальное положительное число равно

А = 2 31 – 1 = 2147483647₁₀.

Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.

Формат с плавающей запятой

Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.

Число в экспоненциальном формате представляется в таком виде:

где $m$ — мантисса числа (правильная отличная от нуля дробь);

$q$ — основание системы счисления;

$n$ — порядок числа.

Например, десятичное число 2674,381 в экспоненциальной форме запишется так:

2674,381 = 0,2674381 ⋅ 10 4 .

Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.

Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.

Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 1111111₂ = 127₁₀. Так как числа представляются в двоичной системе счисления, то

Аналогично, максимальное значение мантиссы равно

Таким образом, диапазон чисел обычной точности составляет $±1.7 · 10^$.