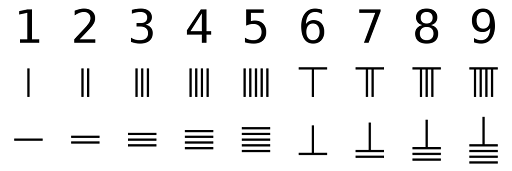
Системы счисления в информатике: виды, примеры, характеристики
Люди постоянно используют числа – абстрактное понятие, применяемое для качественной характеристики и измерения окружающего мира. Одним народам достаточно нескольких цифр: один, два и много, другие разработали десяток способов представления чисел. И первым, и вторым для решения поставленных задач этого достаточно. Кратко рассмотрим виды и историю развития систем счисления (СС). Разберёмся с их классификацией.
Натуральные числа были с людьми всегда. Для подсчёта небольшого количества объектов вязались узлы, использовались камешки – так появились счёты, загибались пальцы. Последние и стали основой десятичной СС.
С появлением необходимости проводить измерения расстояний и габаритов объектов придумали дробные числа. Для измерения времени создали древние системы счисления, привязанные к астрономическим событиям: вращение Земли вокруг Солнца, своей оси, движение Луны, затем полученные величины разбили на более мелкие – часы, минуты. У большинства народов были собственные СС. Римляне обозначали количество буквами алфавита, арабы – современными цифрами.
Греки обозначали цифры буквами алфавита, на которые начинались их названия.
Японцы и китайцы считали палочками.
Язык как способ представления и передачи информации
Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.
В зависимости от способа восприятия знаки делятся на:
- зрительные (буквы и цифры, математические знаки, музыкальные ноты, дорожные знаки и др.);
- слуховые (устная речь, звонки, сирены, гудки и др.);
- осязательные (азбука Брайля для слепых, жесты-касания и др.);
- обонятельные;
- вкусовые.
Для долговременного хранения знаки записывают на носители информации.
Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).
По способу связи между формой и значением знаки делятся на:
- иконические — их форма похожа на отображаемый объект (например, значок папки «Мой компьютер» на «Рабочем столе» компьютера);
- символы — связь между их формой и значением устанавливается по общепринятому соглашению (например, буквы, математические символы ∫, ≤, ⊆, ∞; символы химических элементов).
Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.
Языки делятся на:
- естественные (разговорные) — русский, английский, немецкий и др.;
- формальные — встречающиеся в специальных областях человеческой деятельности (например, язык алгебры, языки программирования, электрических схем и др.)
Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.
Введение в двоичную систему счисления
Компьютер использует биты для представления информации. Бит — это самая основная единица хранения в компьютере. Важный компонент компьютеров называется транзистором. Так же, как выключатель света, транзистор либо пропускает, либо предотвращает протекание тока. Итак, у него всего два состояния: включено и выключено.
Каждое число в компьютере — это электрический сигнал. На заре компьютеров электрические сигналы представляли собой состояние «включено» (отрицательный заряд) и состояние «выключено» (положительный заряд). Это образует своего рода бинарный переключатель.
Эти два состояния могут быть представлены одним из двух символов: 1 и 0. Это означает, что основание двоичной системы счисления равно 2. Для представления каждого числа нужны только символы.
Базовые цифры для двоичной системы просты: 0 для представления низкого состояния и 1 для представления высокого состояния.
Вместо того, чтобы представлять числа как отдельные единицы (например, число 10 или 400), мы используем группы единиц и нулей. Например, вот как это выглядит, когда компьютер считает до 10:

Это называется двоичной системой счисления. Каждая двоичная цифра называется битом. Когда дело доходит до размещения значений и цифр в этой системе, мы размещаем значения, соответствующие возрастающей степени 2 слева направо.
Самая правая цифра называется младшим значащим битом (LSB), а крайняя левая цифра — самым старшим битом (MSB).
Вы можете манипулировать битами влево и вправо с помощью побитовых операторов, чтобы эффективно изменять значение числа на уровне машинного кода.
Преобразование между десятичным и двоичным числами
Теперь, когда мы знаем основы двоичной системы, давайте узнаем, как преобразовывать десятичную систему в двоичную. Начнем с преобразования двоичного числа в десятичное.
Мы знаем, что двоичная система имеет разрядные значения степени 2. Эти значения являются весами для цифр (0 или 1) в этих позициях. Вот как это работает:
Умножаем каждую цифру на ее вес (ее позиция умножаем на 2)
Суммируем их все, чтобы получить десятичное число
Итак, возьмем двоичное число 11111010 и переведем его в десятичную систему счисления.




Теперь попробуем наоборот. Как преобразовать десятичное число в двоичное? Один из способов сделать это — повторное деление, что очень удобно.
Итак, возьмем число 19. Начнем с деления его на два и выписки остатка. Когда мы разделим 19 на 2, мы получим 9 с остатком 1.
Затем мы берем 9 и делим его на 2, что дает нам результат 4 с остатком 1. Этот процесс продолжается до тех пор, пока мы не дойдем до нуля. Остатки, которые мы собрали, составляют наше двоичное число!

Многократное деление на 2 и отслеживание остатков — это быстрый способ преобразования десятичной дроби в двоичную!
Как переводить двоичные числа в десятичные
Разберемся, как быстро переводить двоичные числа в десятичные. Для примера потребуется достаточно большое двоичное число, чтобы мы не могли вычислить его на пальцах.

Запишем его в математической записи, помня, что вместо основания 10, мы используем основание 2.
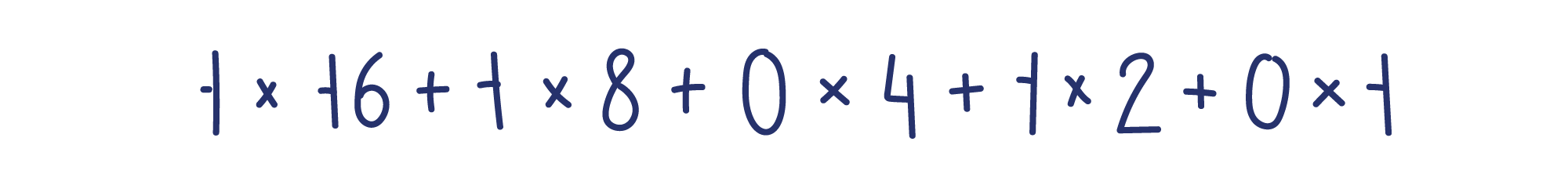
Из этого примера видно, что у всех слагаемых только два множителя — 0 и 1. Слагаемые с множителем 0 равны нулю, поэтому их можно отбросить, оставив только слагаемые с множителем 1.
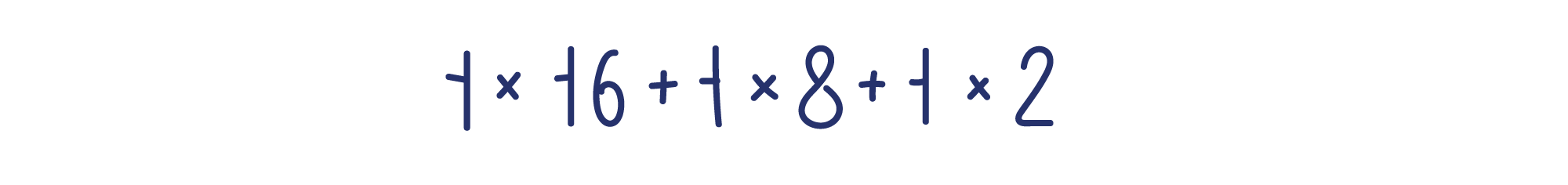
У слагаемых с множителем 1 этот множитель можно не записывать.
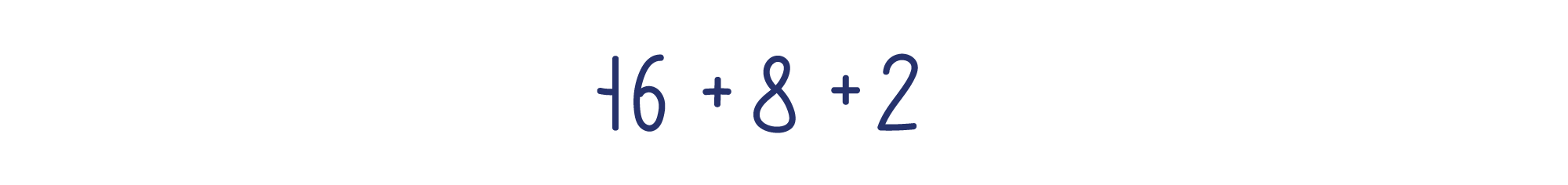
Теперь нетрудно посчитать сумму.

Вывод: число 11010 в двоичной записи — то же самое, что 26 в десятичной.
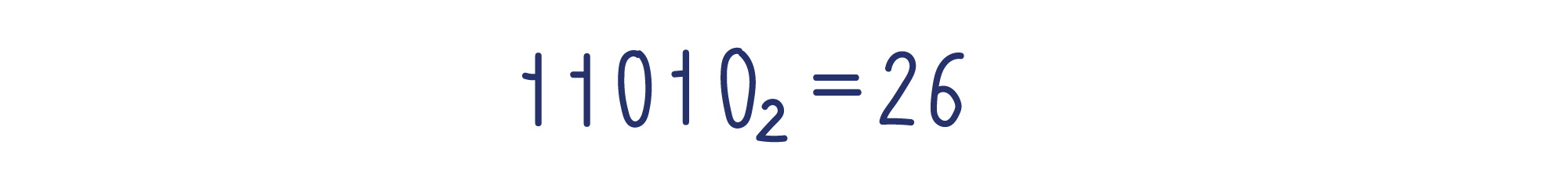
Ещё раз повторим, как перевести двоичное число в десятичное.
- Записать число в математическом виде
- Отбросить слагаемые с множителем 0
- Сложить результат
Программисты иногда запоминают некоторые степени числа два, чтобы уметь оценивать порядок двоичных чисел. Вы можете подглядывать в эту таблицу:
| Двоичное число | Степень 2 | Десятичное число |
|---|---|---|
| 12 | 2 0 | 1 |
| 102 | 2 1 | 2 |
| 1002 | 2 2 | 4 |
| 10002 | 2 3 | 8 |
| 1 00002 | 2 4 | 16 |
| 10 00002 | 2 5 | 32 |
| 100 00002 | 2 6 | 64 |
| 1000 00002 | 2 7 | 128 |
| 1 0000 00002 | 2 8 | 256 |
| 10 0000 00002 | 2 9 | 512 |
| 100 0000 00002 | 2 10 | 1 024 |
| 1 0000 0000 0000 00002 | 2 16 | 65 536 |
| 1 0000 0000 0000 0000 0000 00002 | 2 24 | 16 777 216 |
| 1 0000 0000 0000 0000 0000 0000 0000 00002 | 2 32 | 4 294 967 296 |
С помощью этой таблицы можно переводить числа из двоичной системы в десятичную практически «в уме».
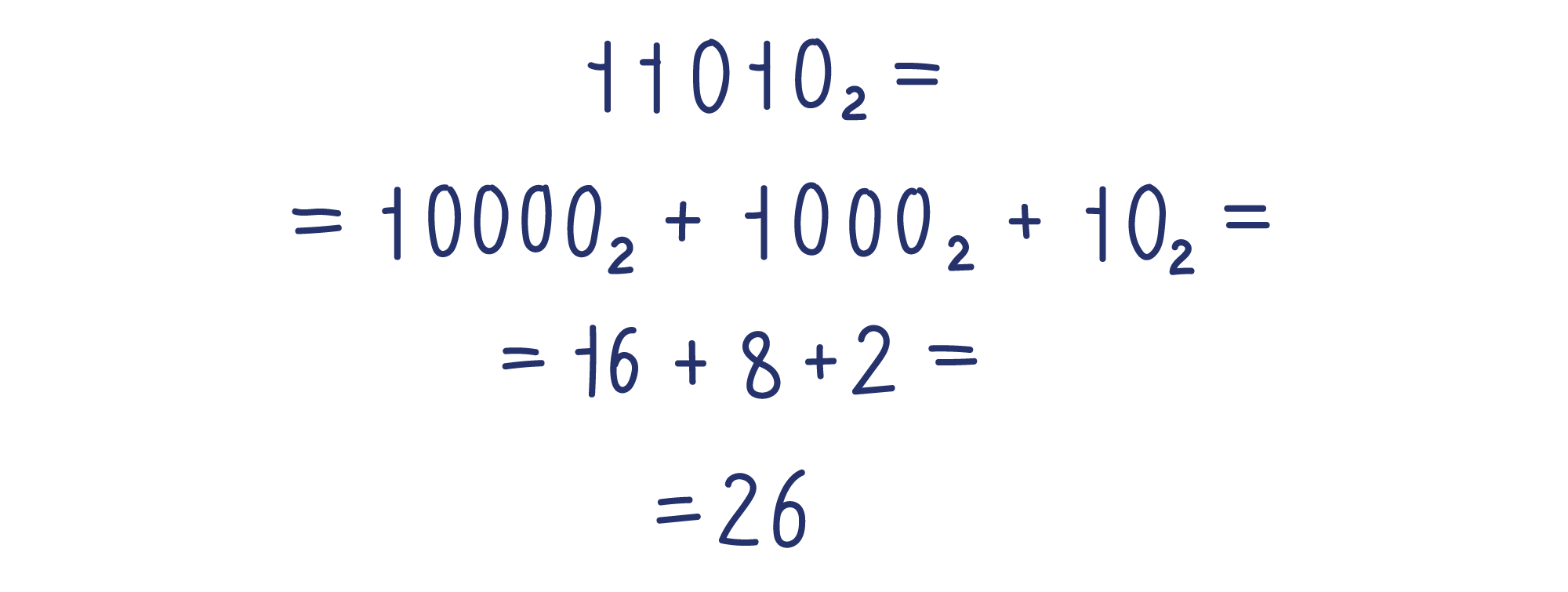
Целые числа в компьютере
Правило № 4: в памяти компьютера числа хранятся в двоичной системе счисления*. С двоичной системой счисления вы знакомы из курса информатики 7-9 классов. Например, если под целое число выделяется ячейка памяти размером в 16 битов, то самое большое целое положительное число будет таким:

В десятичной системе счисления оно равно:
2 15 — 1 = 32 767.
-
перевести число 32 768 в двоичную систему счисления; это легко, поскольку 32768 = 2 15 :

Единица в первом бите обозначает знак «минус». Не нужно думать, что полученный код — это «минус ноль». Этот код представляет число -32 768. Таковы правила машинного представления целых чисел. Данное представление называется дополнительным кодом.
Если под целое число в памяти компьютера отводится N битов, то диапазон значений целых чисел:

то есть ограниченность целого числа в компьютере возникает из-за ограничений на размер ячейки памяти. Отсюда же следует и конечность множества целых чисел.
Мы рассмотрели формат представления целых чисел со знаком, т. е. положительных и отрицательных. Бывает, что нужно работать только с положительными целыми числами. В таком случае используется формат представления целых чисел без знака. В этом формате самое маленькое число — ноль (все биты — нули), а самое большое число для 16-разрядной ячейки:

В десятичной системе это 2 16 — 1 = 65 535, примерно в два раза больше по модулю, чем в представлении со знаком.
Из всего сказанного делаем вывод: целые числа в памяти компьютера — это дискретное, ограниченное и конечное множество.
Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака. Шаг в компьютерном представлении последовательности целых чисел, как и в математическом, остается равным единице.
Рисунок 1.7 отражает то обстоятельство, что при переходе от математического представления множества целых чисел к представлению, используемому в информатике (компьютере), происходит переход к ограниченности и конечности.

Рис. 1.7. Представление о множестве целых чисел в математике и в информатике
Представление вещественных чисел
- 472000000=4,72⋅10 8
- 472000000=47,2⋅10 7
- 472000000=472,0⋅10 6
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида:4,72E+8.
Здесь знак E обозначает основание десятичной системы счисления и читается как «умножить на десять в степени». Из приведённого выше примера видно, что положение запятой в записи числа может изменяться. Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472000000 будет представлено как 0,472⋅10 9 .
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядки и мантиссы. Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112=12710 и, следовательно, максимальное значение числа: 0,11111111111111111111111⋅10 1111111 .
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
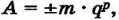
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Дополнительный код
Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0 000 1010 —-> -10 = 1 000 1010
Инвертируем значение (получаем обратный код):
1 000 1010 —-> 1 111 0101
К полученной инверсии прибавляем 1:
1 111 0101 + 1 = 1 111 0110 — десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0 000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1 111 0110 — десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода












