Какие системы счисления используются для представления информации в компьютерах

Доклад Системы счисления по информатике 5, 8 класс сообщение

Мы привыкли к цифрам, которые называются арабскими. Называются они так, потому что впервые были обоснованны и напечатаны на арабском языке. Это несложно и не составляет проблем для понимания. В системе счисления эти же самые цифры будут называться десятичными. Почему? Ответ на этот вопрос также не труден. Всё потому, что при счёте мы используем всего 10 цифр от 0 до 9, а затем они начинают повторяться.

Но десятичная система счисления – не единственная. Их существует множество. Рассмотрим самые популярные из них:

Двоичная система счисления

В этой системе счисления используются только две цифры: 0 и 1. Единица представляет собой степень двойки. Чем больше единиц в записи, тем больше число. На двоичной системе вычисления построена работа многих современных вычислительных машин. Например, число 1001 в двоичной системе счисления, это тоже самое что 9 в десятичной. Расчёт ведётся так: справа – налево в двоичном числе проставляются степени, затем единицы «заменяются» на двойки возводятся в степень и складываются между собой. Так, если мы проведём эту процедуру с числом 1001. То мы получим: 2 в 0 степени + 2 в третьей степени или 1 + 8 получим 9.

Пятеричная система счисления

В этой системе счисления существует всего пять цифр. Поэтому основанием данной системы является пятёрка. Чтобы возвести число из десятичной системы в пятеричную, необходимо делить это число на пять записывая остатки. После того, как при делении не останется целой части, деление прекращается, а остатки складываются снизу вверх. Например число 24( 10-чная система счисления) в пятеричной системе будет выглядеть как 44. 24/5 = 4 и 4 в остатке. 4/5 = 0 и 4 в остатке, остатки записываем считая снизу вверх. То есть, если бы при первом делении у нас получилось пять, то число выглядело бы как 45, а не 54.

Восьмеричная система счисления

В ней действуют все те же законы и правила, что и в пятеричной. Единственным отличием является только то, что основанием системы здесь является восьмёрка, тот же принцип, существует и во всех остальных системах счисления, для наглядности, переведём число 45 десятичной системы в восьмеричную: 45/8 = 5 и 5 остаток. 5/8 = 0 и 5 остаток. В итоге получается число 55. В шестнадцатеричной системе это число будет выглядеть как 2D( после 9 все числа заменяются на буквы английского алфавита по порядку A – 10 B -11 C – 12 и так далее).

От десятичных чисел к двоичным

Разберемся, как устроена десятичная система, на примере произвольного большого числа.

1072

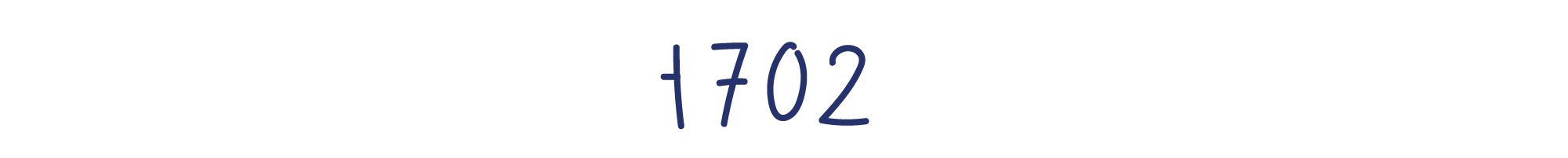
Это четырехзначное число, потому что оно состоит из четырёх цифр. И, поскольку речь идёт о десятичной системе, мы можем использовать десять различных цифр.

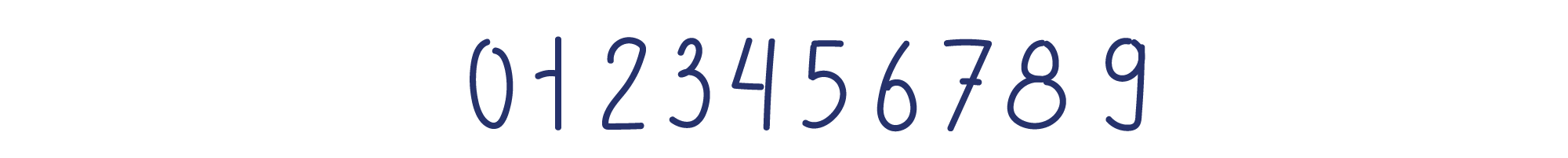
0123456789

Величина, которая скрывается за каждой цифрой, зависит от её позиции, поэтому такую систему счисления называют также и позиционной. Справа мы записываем самые младшие значения — единицы, слева от них десятки, затем сотни, и так далее. Запись 1702 означает буквально следующее.

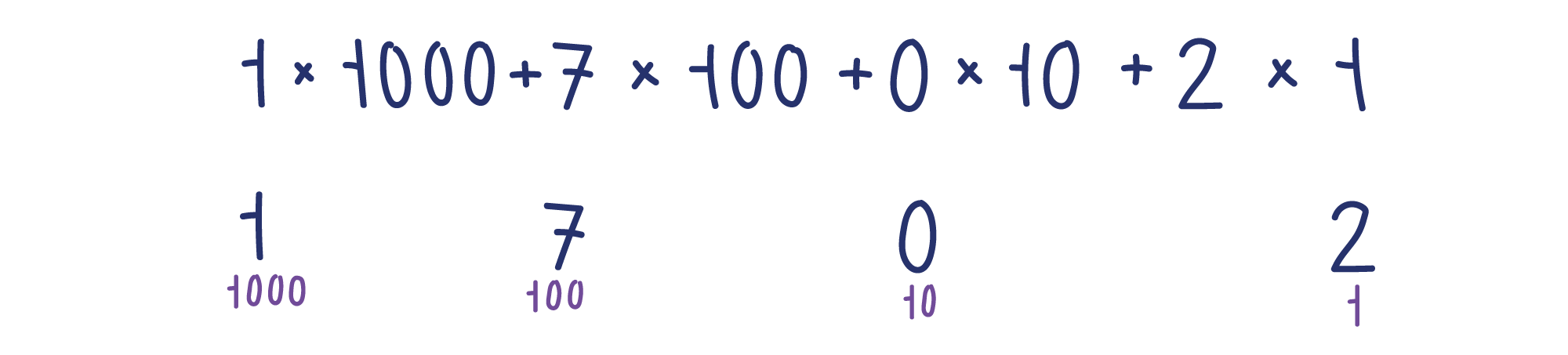
1×1000+7×100+0×10+2×1

Цифры, записанные в соседних позициях, различаются в десять раз — это и есть десятичная система. Однако, как мы говорили ранее, привычная нам десятичная система — далеко не единственная. Однако, опираясь на неё, нам будет проще понять принципы работы других систем счисления. Например, для записи того же самого числа 1702 в двоичной системе надо придерживаться тех же правил, но вместо десяти цифр нам потребуется всего две — 0 и 1.

Цифры, записанные в соседних позициях, будут различаться не в десять раз, а в два. То есть там, где в десятичной системе мы видим 1, 10, 100, 1 000, 10 000, в двоичной будут числа 1, 2, 4, 8, 16 и так далее.

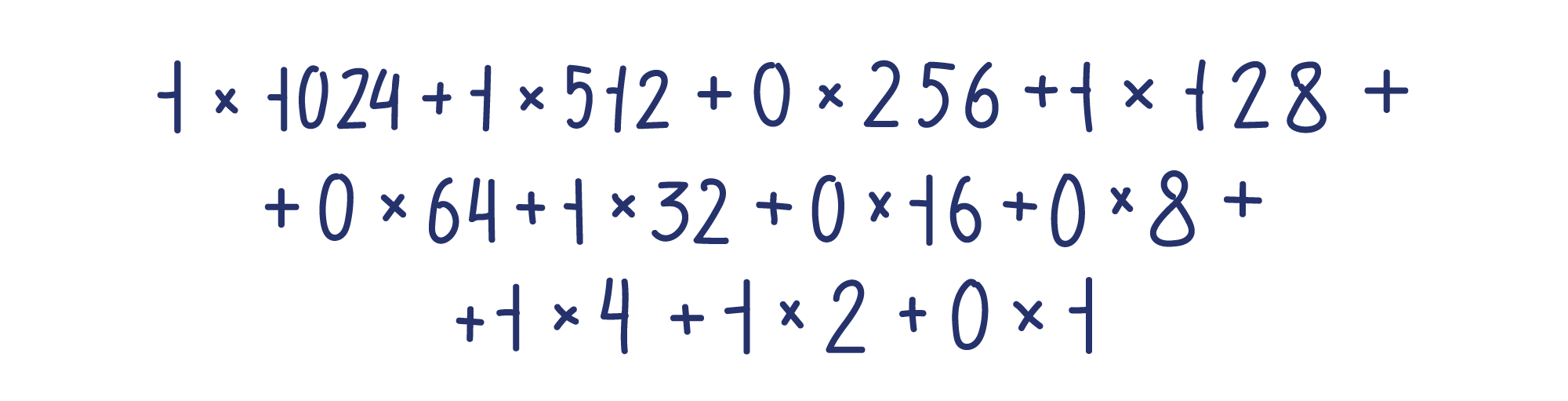
1×1024+1×512+0×256+ +1×128+0×64+1×32+0×16+ +0×8+1×4+1×2+0×1

Это очень большое двоичное число. Давайте запишем его в привычной форме:

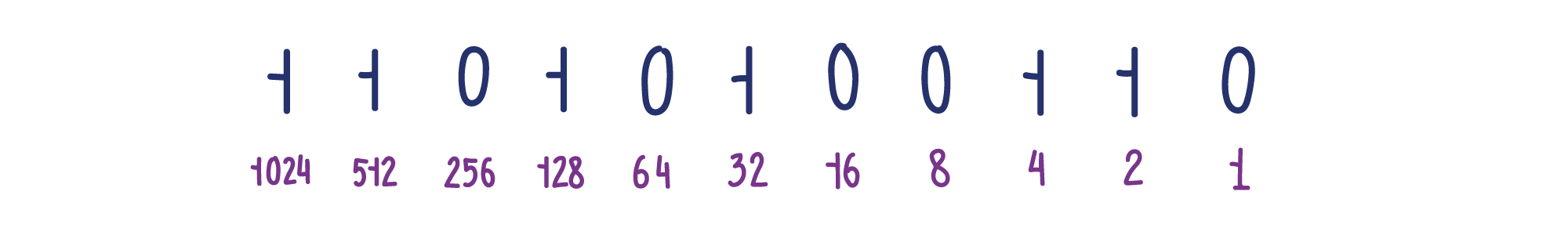
1 1 0 1 0 1 0 0 1 1 0 1024 512 256 128 64 32 16 8 4 2 1

Это число могло бы быть очень большим десятичным числом, потому что состоит из тех же цифр. Чтобы отличать двоичные числа от десятичных, в качестве индекса у них указывают основание системы счисления, то есть 2.

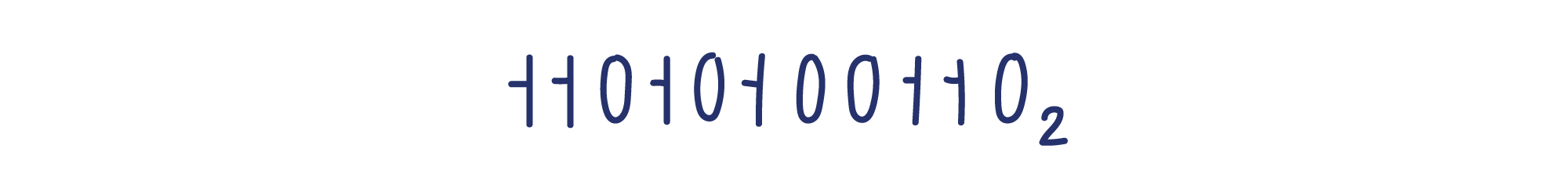
11010100110₂

Это особенно важно, когда в тексте одновременно встречаются десятичные и двоичные числа.

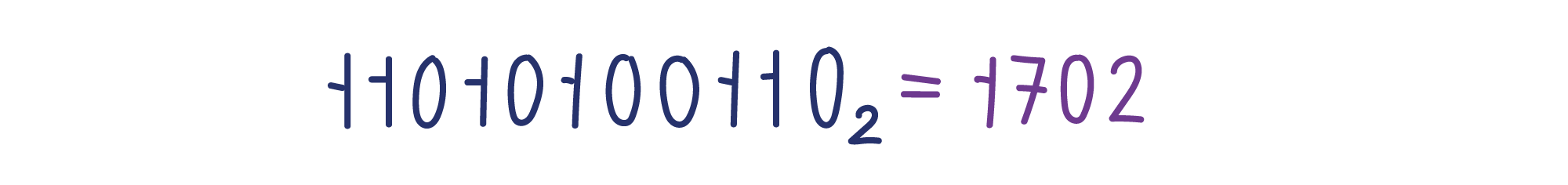
11010100110₂ = 1702

Определение и виды систем счисления

Возможность записать все числа в нужном диапазоне.
Естественность представления – любой из комбинаций соответствует только одно значение.
Обеспечение простоты восприятия и выполнения операций над числами.
Возможность точного (без или с минимальными погрешностями) перевода значений в другие СС.

Различают два типа систем счисления: позиционные, унарные.

Выберите верный вариант: знаки, с помощью которых записываются числа в системе счисления, называются:

Алфавитом.
Основанием.
Числовым рядом.

1. Представление чисел в языке Ruby

5.1. Представление чисел в языке Ruby Если вы знакомы с любым другим языком программирования, то представление чисел в Ruby не вызовет у вас никакого удивления. Объект класса Fixnum может представлять число со знаком или без знака:237 # Число без знака (положительное).+237 # То же, что

11.20. Представление больших чисел фиксированного размера ПроблемаТребуется выполнить операции с числами, размер которых превышает размер типа long int.РешениеШаблон BigInt в примере 11.38 использует bitset из заголовочного файла <bitset> для того, чтобы можно было представить целые

Электронное приложение к уроку

Презентация «Представление информации в компьютере» (Open Document Format)

Ссылки на ресурсы ЕК ЦОР

интерактивный задачник, раздел «Системы счисления» (128659);
http://school-collection.edu.ru/catalog/res/fc77f535-0c00-4871-b67c-fa2ecf567d46/?inter
демонстрация к лекции «Представление целых чисел в памяти компьютера» (119430);
http://school-collection.edu.ru/catalog/res/ecf4ab69-d8ac-40a8-b26a-2780aa70b33d/?inter
тест по теме «Системы счисления» — «Система тестов и заданий N12» (134887);
http://school-collection.edu.ru/catalog/res/6e89032a-2e09-4519-bb1e-653b4ecfd08f/?inter
интерактивный задачник, раздел «Представление чисел» (119410);
http://school-collection.edu.ru/catalog/res/c4939f11-5709-4fde-bc83-ceb614135d81/?inter
тренировочный тест «Двоичная система счисления и представление чисел в памяти компьютера» (119342);
http://school-collection.edu.ru/catalog/res/19d0fb95-871d-4063-961d-e7dc5725e555/?inter
информационный модуль «Достоинcтва и недостатки двоичной системы счисления при использовании ее в компьютере»
http://fcior.edu.ru/card/23457/dostoinctva-i-nedostatki-dvoichnoy-sistemy-schisleniya-pri-ispolzovanii-ee-v-kompyutere.html

Федеральный центр информационных образовательных ресурсов:

информационный модуль «Число и его компьютерный код»;
http://fcior.edu.ru/card/11501/chislo-i-ego-kompyuternyy-kod.html
практический модуль «Число и его компьютерный код»;
http://fcior.edu.ru/card/9581/chislo-i-ego-kompyuternyy-kod.html
информационный модуль «Дополнительный код числа. Алгоритм получения дополнительного кода отрицательного числа»;
http://fcior.edu.ru/card/14187/dopolnitelnyy-kod-chisla-algoritm-polucheniya-dopolnitelnogo-koda-otricatelnogo-chisla.html
информационный модуль «Числа с фиксированной и плавающей запятой»;http://fcior.edu.ru/card/2107/chisla-s-fiksirovannoy-i-plavayushchey-zapyatoy.html

liniya

Презентации, плакаты, текстовые файлы

Вернуться к материалам урока

Ресурсы ЭОР

liniya

Cкачать материалы урока

Восьмеричная система

Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.

Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.

Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.

Общие сведения

Числа записывают при помощи определенных математических символов, значение которых зависит от системы счисления (формы представления). Последней называется метод записи числа посредством определенной совокупности знаковых элементов — цифр. Не все учащиеся понимают отличие цифры от числового значения. В учебнике по информатике для 9 класса можно встретить и такое определение: системы счисления — набор символов, используемый для обозначения цифр.

Цифра — определенный математический символ, который указывает на конкретную величину. Они составляют число, а их расположение называется разрядной сеткой.

Цифры классифицируются на 2 вида: арабские и римские. Первые применяются для устного счета и представлены диапазоном от 0 до 9, который называется десятичной формой представления. Римские имеют другие обозначения. Вот расшифровка некоторых из них, которую можно перечислить в виде следующих символов: 1 — I, 2 — II, 3 — III, 4 — IV, 5 — V, 6 — VI, 7 — VII, 8 — VIII, 9 — IX, 10 — X, 40 — XL, 50 — L, 90 — XC, 100 — C, 200 — CC, 400 — CD, 500 — D.

Самое главное

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, при помощи которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.

Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Основанием позиционной системы счисления может служить любое натуральное число q > 1.

В позиционной системе счисления с основанием q любое число может быть представлено в виде: