Считайте в уме как компьютер (2006, Билл Хэндли)

Как научиться быстро считать в уме?

Как давно вы считали в уме, а не столбиком, и уж тем более не с помощью калькулятора? Между прочим, считать в уме не только модно, но и полезно: так вы развиваете краткосрочную память, концентрацию и внимание. А ещё, какой же кайф испытываешь, когда можешь посчитать, сколько тебе должны дать сдачи, пока стоишь в очереди, м-м-м…

Всего несколько месяцев ежедневных тренировок по 5-10 минут, и вы почувствуете, как ускорился ваш мозг.

Магия чисел. Моментальные вычисления в уме и другие математические фокусы (2014, ы: Артур Бенджамин)

Эта книга научит вас считать в уме быстрее, чем на калькуляторе, запоминать большие числа и получать от математики удовольствие. Любой человек может умножать, делить, возводить в степень и производить другие операции над большими числами в уме и с большой скоростью. Для этого не нужно решать десятки тысяч примеров и учиться годами — доста .

ISBN: 978-5-00057-270-2
Формат: PDF, OCR без ошибок
Авторы: Артур Бенджамин, Майкл Шермер
Год выпуска: 2014
Жанр: Научно-популярная литература
Издательство: Манн, Иванов и Фербер
Язык: Русский
Количество страниц: 320

ПАРТНЕРЫ

«Неожиданные вспоминания» Дмитрия и Инги Медоустов — это настоящее «густое» чтение, поэзия не слов, но состояний, состояний «вне ума», состояний мимолетных и трудноуловимых настолько же, насколько они фундаментальны. Состояний, в которых авторы тем не менее укоренены и укореняются именно (хотя и не только) через писание.

Эта детская книжечка — вполне «семейная». Автор посвятил ее своим маленьким брату и сестричке. И в каком-то смысле она может служить эталоном «фамильной книги», предназначенной для внутреннего, семейного круга, но — в силу своей оригинальности — интересной и сторонним людям.

История, рассказанная в этой очень необычно оформленной книге, действительно может быть названа «ботанической», поскольку немало страниц в ней посвящено описанию редких для нас южных растений. Впрочем, есть достаточно резонов назвать ее также «детективной», или «мистической», или «невыдуманной».

Сборник рассказов московского писателя Сергея Триумфова включает страстные лирические миниатюры, пронзительные и яркие психологические истории и своеобразные фантазии-размышления на извечные темы человеческого бытия.

Книга прозы Александра Попова (директора челябинского физико-математического лицея №31) «Судный день» – это своего рода хроника борьбы и отчаяния, составленная человеком, прижатым к стенке бездушной системой. Это «хождения по мукам» души измученной, но не сломленной и не потерявшей главных своих достоинств: умения смеяться и радоваться, тонуть в тишине и касаться мира – глазами ребенка.

Роберто Бартини — человек-загадка. Кем он был — гениальным ученым, на века опередившим свое время, мыслителем от науки, оккультным учителем? Этот материал — только краткое введение в судьбу «красного барона».

«Люди спрашивают меня, как оставаться активным. Это очень просто. Считайте в уме ваши достижения и мечты. Если ваших мечтаний больше, чем достижений – значит, вы все еще молоды. Если наоборот – вы стары. «

«Отец Александр [Мень] видел, что каждый миг жизни есть чудо, каждое несчастье – священно, каждая боль – путь в бессмертие. А тем более цветок или дерево – разве не чудо Божье? Он говорил: если вам плохо, пойдите к лесу или роще, возьмите в руку ветку и так постойте. Только не забывайте, что это не просто ветка, а рука помощи, вам протянутая, живая и надежная. «

«Всего Капица написал Сталину 49 писем! Сталин не отвечал, но когда Капица, не понимая такой невоспитанности, перестал ему писать, Маленков позвонил Капице и сказал: «Почему вы не пишете Сталину, он ждет новых писем». И переписка (односторонняя) возобновилась».

«Есть английское слово immaculate, «безупречно». К этому, очевидно, стремился Вадим. «

«Через цвет происходит таинственное воздействие на душу человека. Есть святые тайны — тайны прекрасного. Понять, что такое цвет картины, почувствовать цвет – все равно, что постигнуть тайну красоты».

«. Ненависть, если и объединяет народ, то на очень короткое время, но потом она народ разобщает еще больше. Неужели мы будем патриотами только из-за того, что мы кого-то ненавидим?»

«Внутреннее горение. Отказ от комфорта материального и духовного, мучительный поиск ответов на неразрешимые вопросы… Где все это в современном мире? Наше собственное «я» закрывает от нас высшее начало. Ведь мы должны быть свободными во всех своих проявлениях. Долой стеснительность. «

«В 1944 году по Алма-Ате стали ходить слухи о каком-то полудиком старике — не то гноме, не то колдуне, — который живет на окраине города, в земле, питается корнями, собирает лесные пни и из этих пней делает удивительные фигуры. Дети, которые в это военное время безнадзорно шныряли по пустырям и городским пригородам, рассказывали, что эти деревянные фигуры по-настоящему плачут и по-настоящему смеются…»

«Для Beatles, как и для всех остальных в то время, жизнь была в основном черно-белой. Я могу сказать, что ходил в школу, напоминавшую Диккенса. Когда я вспоминаю то время, я вижу всё черно-белым. Помню, как зимой ходил в коротких штанах, а колючий ветер терзал мои замерзшие коленки. Сейчас я сижу в жарком Лос-Анджелесе, и кажется, что это было 6000 лет назад».

«В мире всегда были и есть, я бы сказал так, люди этического действия – и люди корыстного действия. Однажды, изучая материалы по истории Челябы, я задумался и провел это разделение. Любопытно, что в памяти потомков, сквозь время остаются первые. Просто потому, что их действия – не от них только, они в унисон с этикой как порядком. А этический порядок – он и социум хранит, соответственно, социумом помнится».

«Я не турист. Турист верит гидам и путеводителям… А путешественник — это другая категория. Во-первых, ты никуда не спешишь. Приходишь на новое место, можешь осмотреться, пожить какое-то время, поговорить с людьми. Для меня общение по душам – это самое ценное в путешествии».

«В целом мире нет ничего больше кончика осенней паутинки, а великая гора Тайшань мала. Никто не прожил больше умершего младенца, а Пэнцзу умер в юном возрасте. Небо и Земля живут вместе со мной, вся тьма вещей составляет со мной одно».

«Я про Маленького принца всю жизнь думал. Ну не мог я его не снять! Были моменты, когда мальчики уставали, я злился, убеждал, уговаривал, потом ехал один на площадку и снимал пейзажи. Возможно, это одержимость. «

«Невероятная активность Запада во всем происходящем не имеет ничего общего ни со стремлением защищать права человека на Украине, ни с благородным желанием помочь «бедным украинцам», ни с заботой о сохранении целостности Украины. Она имеет отношение к геополитическим стратегическим интересам. И действия России – на мой взгляд – вовсе не продиктованы стремлением «защитить русских, украинцев и крымских татар», а продиктованы все тем же самым: геополитическими и национальными интересами».

© Информационно-образовательная группа www.Zenon74.ru (Издательский Дом Игоря Розина), 2011
Все права на материалы, размещенные на сайте, защищены и охраняются законами РФ
Полное или частичное использование любых материалов сайта в электронных СМИ, а также в печатном виде возможно только с письменного разрешения редакции info@zenon74.ru

При использовании любых материалов сайта в электронных СМИ обязательно наличие активной гипертекстовой ссылки.

Редакция может не разделять точку зрения авторов, комментаторов и героев материалов

Ответственность за содержание рекламных объявлений, размещенных на веб-сайте, несет рекламодатель

Более сложные методики

Эффективность умножения в уме некоторых двузначных чисел может быть выше за счет меньшего количества действий, если использовать специальные алгоритмов. Ниже представлены три специальные методики, в том числе введение и использование опорного числа.

Квадрат суммы и квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности . Например:

23 2 = (20+3) 2 = 20 2 + 2×3×20 + 3 2 = 400+120+9 = 529

69 2 = (70-1) 2 = 70 2 – 70×2×1 + 1 2 = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5, необходимо число до последней пятерки, умножить на сумму этого же числа и единицы . К результату дописываем 25. Вот несколько примеров:

25 2 = (2×(2+1)) 25 = 625

85 2 = (8×(8+1)) 25 = 7 225

155 2 = (15×(15+1)) 25 = (15×16)25 = 24 025

Опорное число

Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. А методика использования этого числа зависит от того, являются ли множители больше или меньше него самого.

Оба множителя меньше опорного. Допустим, мы хотим умножить 48 на 47 . Эти числа находятся достаточно близко к числу 50 , а следовательно удобно использовать 50 в качестве опорного числа. Далее действуем так: из 47 вычетаем столько, сколько не хватает 48 до 50 (либо из 48 вычетаем столько, сколько не хватает 47 до 50 ), полученный результат умножаем на опорное число и прибавляем к нему произведение разностей опроного числа с каждым сомножителем. Наглядный пример:

( 48 –( 50 — 47 ))× 50 + ( 50 — 47 )×( 50 — 48 ) = 2250 + 6 = 2256

Оба множителя больше опорного. Действовать нужно точно так же, но не вычитать недостаток, а прибавлять избыток:

( 51 +( 63 — 50 ))× 50 + ( 63 — 50 )×( 51 — 50 ) = 3200 + 13 = 3213

Один множитель меньше, другой больше опорного. Схема та же, но произведение недостатка и избытка нужно вычитать:

( 45 +( 52 — 50 ))× 50 – ( 52 — 50 )×( 50 — 45 ) = 2350 – 10 = 2340

Умножение чисел, которые оканчиваются на ноль

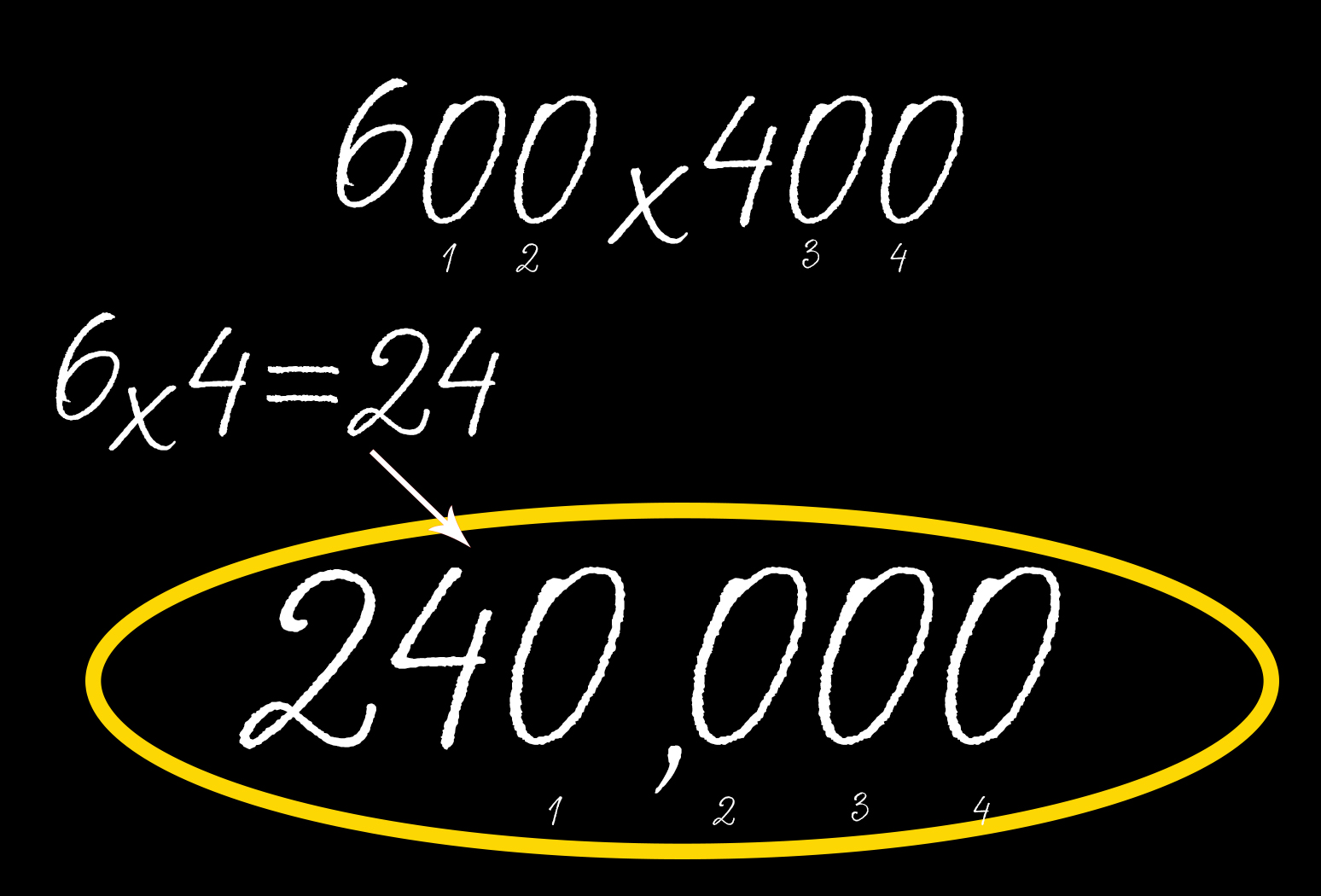
Примеры с большими пугающими числами, которые оканчиваются на ноль, тоже легко решить с помощью специального приема. Согласно education.cu-portland.edu, нужно просто «вычеркнуть» нули из примера, а в конце вновь их добавить.

Если вы умножаете 600 на 400, уберите все нули и перемножьте 6 на 4. Получится 24. Затем подсчитайте общее количество нулей в исходном уравнении и припишите их к полученному значению. Так как в нашем примере было четыре нуля, то ответ будет равен 240000.

Способы быстрого счета

Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:

Вычитание 7, 8, 9

Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.

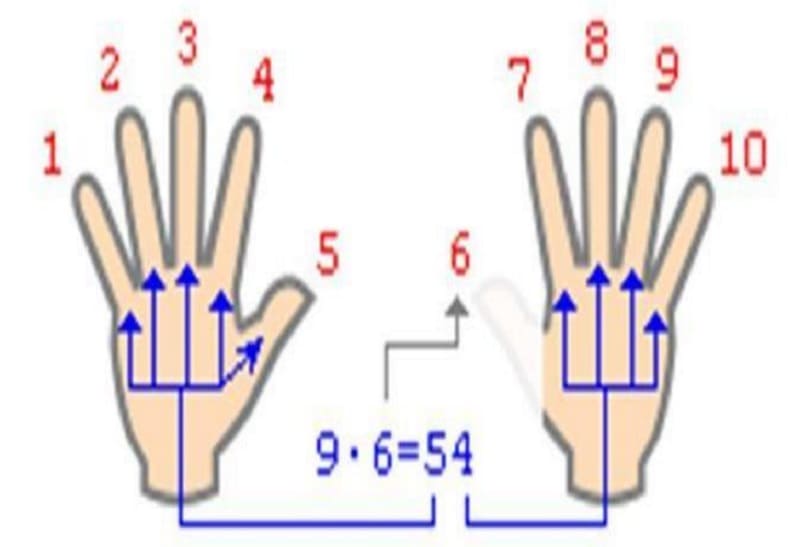
Умножение на 9

Быстро умножить любое число на 9 можно при помощи пальцев рук.

Деление и умножение на 4 и 8

Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.

Например, 46*4=46*2*2 =92*2= 184.

Умножение на 5

Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.

Умножение на 25

Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.

Умножение на однозначные числа

Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.

Например, умножим 83*7.

Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.

Возьмем более сложный пример: 236*3.

Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.

Определение диапазонов

Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).

Раскладка на десятки и единицы

Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия:

1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.

Схематично это можно описать так:

— Первое действие: 60*80 = 4800 — запоминаем
— Второе действие: 60*5+3*80 = 540 – запоминаем
— Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.

Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

• Контрольная работа от 1 дня / от 120 р. Узнать стоимость
• Дипломная работа от 7 дней / от 9540 р. Узнать стоимость
• Курсовая работа 5 дней / от 2160 р. Узнать стоимость
• Реферат от 1 дня / от 840 р. Узнать стоимость

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Полезные арифметические правила:

1. Вычитание

+ При отнимании 9 от любого числа из него вычитают 10 и добавляют 1:
N-10+1
321-9 = 321-10+1 = 312

+ При отнимании 8 от любого числа из него вычитают 10 и добавляют 2:
N-10+2
321-8 = 321-10+2 = 313

+ При отнимании 7 от любого числа из него вычитают 10 и добавляют 3:
N-10+3
321-7 = 321-10+3 = 314

2. Умножение и деление

+ Любые числа умножаются на 9 легко и просто: следует умножить заданное число на 10 (или просто приписать ноль), а от полученного числа отнять исходное:
Nх9 = Nx10 – N
63х9 = 630 – 63 = 567
Это самый быстрый способ произвести подобные вычисления. Его рекомендуем довести до полного втомата.

+ Некруглые числа умножаются на 2 таким нехитрым способом:
сначала их округляют до удобных для умножения ближайших значений. Например, если необходимо посчитать 149х2, то проще для начала умножить 150 на 2, а после вычесть из результата 2 (1х2 = 2 – ведь это 1 не хватало нам до 150). Итого получаем пример:
149х2 = 150х2 — (1х2) = 298

+ По схожему принципу можно делить на 2 некруглые числа: округляется число, которое делят на 2, и из него вычитают. Делим это число на 2-ку, отнимаем 1 (последняя цифра получена в процессе деления прибавленной 2-ки на 2-ку.
В результате деление 198 на 2 равняется: 200:2 – 2:2 = 100 – 1 = 99!

+ Умножение, как и деление на 4 и 8, соответствуют двукратному и трехкратному умножению и делению на 2 в каждом случае конкретном случае. Действия производятся последовательно, например:
26х4 = 26х2х2 = 52х2 = 104
88/8 = 88/2/2/2 = 44/2/2 = 22/2 = 11

+ Математики вывели закономерность, по которой умножение на 5 практически приравнивается к делению на 2. Пример: 33х5 = 165, 33:2 = 16,5
Из этого следует, что при умножении на 5 любого из чисел, его стоит разделить на 2, а после этого умножить на 10:
68х5 = 68:2х10 = 34х10 = 340

+ Чтобы умножить какое-то число на 25, иногда проще его разделить на 4, а после увеличить в 100 раз (или приписать два нуля). Ведь умножение на 25 отчасти эквивалентно делению на 4:
8х25 = 8:4х100 = 200

+ Неслабые трудности при вычислениях в уме представляет умножение двузначных и трехзначных чисел на однозначные. Чтобы справиться и с этим, необходимо разряды многозначных чисел перемножать по очереди (начиная слева направо). При умножении 54 на 3 для начала перемножаем 5 и 3, дописывая ноль (учтем, что это разряд десятков). После этого складываем результат с произведением 4х3.
54х3 = 5х3х10+4х3 = 150+12 = 162
Попробуем умножить на однозначное трехразрядное число:
541х3 = 5х3х100+4х3х10+1х3 = 1500+120+3 = 1623

Прогнозирование конечного результата при счете в уме

В операциях умножения, особенно если приходится оперировать многозначными числами, можно легко сбиться с толку и ошибиться с результатом. Во избежание этого нужно грамотно «прогнозировать» ответ.

• Перемноженные между собой однозначные числа не дадут произведения, большего 81. Ведь 9х9 = 81.
• При умножении двузначных чисел конечный итог не превысит 10 000, так как 99х99 = 9801.
• Произведение двух трехзначных чисел не будет больше 1 000 000. Ведь 999х999 = 998001.
• Важно помнить деление 1000 на 2, 4, 8, 16. Всегда пригодится держать в голове результат деления чисел, кратных 10 и чисел, кратных 2: 1000 = 2х500 = 4х250 = 8х125 = 16х62,5.

Перечисленные выше формулы являются основными для устного счета. Преодоление трудностей со сложными примерами — в регулярных упражнениях. Доведение до автоматизма арифметических операций позволит вам решать просто неподъемные для обычного человека математические задачки. Восхищайте своими интеллектуальными способностями окружающих!