Многие числа обрели свою величину и суеверное значение еще в древности. В наши дни к ним добавляются новые мифы. Существует много легенд о числе пи, немногим уступают ему в известности знаменитые числа Фибоначчи. Но, пожалуй, самым удивительным является число е, без которого не может обойтись современная математика, физика и даже экономика.
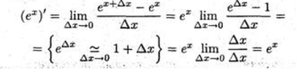
Арифметическое значение числа е равно приблизительно 2,718. Почему не точно, а приблизительно? Потому что это число иррациональное и трансцендентное, его нельзя выразить дробью с натуральными целыми числами или многочленом с рациональными коэффициентами. Для большинства расчетов указанной точности значения в 2,718 достаточно, хотя современный уровень вычислительной техники позволяет определить его значение с точностью более триллиона знаков после запятой.
Главной особенностью числа е является то, что производная его показательной функции f (x) = e x равно значению самой функции е х . Такого необычного свойства нет больше ни у какой другой математической зависимости. Расскажем об этом чуть подробнее.

Что такое предел
Вначале разберемся с понятием предела. Рассмотрим какое-нибудь математическое выражение, например, i = 1/n. Можно увидеть, что при увеличении «n «, значение «i «будет уменьшаться, а при стремлении «n» к бесконечности (которая обозначается значком ∞), «i» будет стремиться к предельному значению (называемого чаще просто пределом), равному нулю. Выражение предела (обозначаемого как lim) для рассматриваемого случая можно записать в виде lim n →∞ (1/ n) = 0 .
Существуют различные пределы для различных выражений. Одним из таких пределов, вошедших в советские и российские учебники как второй замечательный предел, является выражение lim n →∞ (1+1/ n) n . Уже в Средневековье было установлено, что пределом этого выражения является число е.
К первому же замечательному пределу относят выражение lim n →∞ (Sin n / n) = 1.
Как найти производную e x — в этом видео.
Что такое производная функции
Для раскрытия понятия производной следует напомнить что такое функция в математике. Чтобы не загромождать текст сложными определениями, остановимся на интуитивном математическом понятии функции, заключающимся в том, что в ней одна или несколько величин полностью определяют значение другой величины, если они взаимосвязаны. Например, в формуле S = π ∙ r 2 площади круга, значение радиуса r полностью и однозначно определяет площадь круга S.
В зависимости от вида, функции могут быть алгебраическими, тригонометрическими, логарифмическими и др. В них могут быть взаимосвязаны два, три и более аргументов. Например, пройденное расстояние S, которое объект преодолел с равноускоренной скоростью, описывается функцией S = 0,5 ∙ a ∙ t 2 + V ∙ t, где «t» — время движения, аргумент «а» ускорение (может быть как положительной, так и отрицательной величиной) и «V» начальная скорость движения. Таким образом, величина пройденного расстояния зависит от значений трех аргументов, два из которых («а» и «V») постоянны.
Покажем на этом примере элементарное понятие производной функции. Оно характеризует скорость изменения функции в данной точке. В нашем примере это будет скорость движения объекта в конкретный момент времени. При постоянных «а» и «V» она зависит только от времени «t», то есть говоря научным языком нужно взять производную функции S по времени «t».
Этот процесс называется дифференцированием, выполняется путем вычисления предела отношения прироста функции к приросту ее аргумента на ничтожно малую величину. Решения подобных задач для отдельных функций часто является непростым делом и здесь не рассматриваются. Также стоит отметить, что некоторые функции в определенных точках вообще не имеют таких пределов.
В нашем же примере производная S по времени «t» примет вид S’ = ds/dt = а ∙ t + V, из которого видно, что скорость S’ изменяется по линейному закону в зависимости от «t».

Производная экспоненты
Экспонентой называется показательная функция, в качестве основания которой находится число е. Она обычно отображается в виде F (x) = e x , где показатель степени x является переменной величиной. Данная функция обладает полной дифференцируемостью во всем диапазоне вещественных чисел. С ростом x она постоянно возрастает и всегда больше нуля. Обратная к ней функция — логарифм.

Известный математик Тейлор сумел разложить эту функцию в ряд, названный его именем e x = 1 + x/1! + x 2 /2! + x 3 /3! + … в диапазоне x от — ∞ до + ∞.
Закон, базирующийся на этой функции, называется экспоненциальным. Он описывает:
- возрастание сложных банковских процентов;
- увеличение популяции животных и населения планеты;
- время окоченения трупа и многое другое.
Повторим еще раз замечательное свойство данной зависимости — значение ее производной в любой точке всегда равно значению функции в этой точке, то есть (e x )’ = e x .
Приведем производные для наиболее общих случаев экспоненты:
- (e ax )’ = a ∙ e ax ;
- (e f (x) )’ = f'(x) ∙ e f (x) .
Используя данные зависимости, несложно найти производные для других частных видов этой функции.
Некоторые интересные факты о числе е
С этим числом связаны фамилии таких ученых, как Непер, Отред, Гюйгенс, Бернулли, Лейбниц, Ньютон, Эйлер, и другие. Последний собственно и ввел обозначение е для этого числа, а также нашел первые 18 знаков, используя для расчета открытый им ряд е = 1 + 1/1! + 2/2! + 3/3! …
Число e встречается в самых неожиданных местах. Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Видео
Тема видеоурока — производная показательной функции.
Экспонента в жизни- 2. Зачем это нужно?
В прошлом посте мы говорили о том, как пролетели австралийцы с экспонентой.
В этом – постараюсь ответить на главный вопрос жизни Вселенной и все такое.
Где математика экспонента может пригодиться в реальной жизни?
Можно, конечно, скорчить серьезную физиономию и сказать, что,мол:
По экспоненте высыхает земля после дождя, по экспоненте падает давление, когда вы поднимаетесь в горы…. но звучит это как-то по-ботански!
Мало, кто считает диаграммы, придя домой.
Открою страшную тайну:
Вряд ли в жизни придется услышать такое:
— Дайте мне (7! – 6^2+3e^0)^1/4 помидоров и (ln (e^3) ) картофеля, пожалуйста.
— Молодой человек, я не понимаю.
— Мне плевать, я учился не напрасно.
Да, сами по себе занятия математикой неплохо качают мозги (об этом в следующих постах)
Но, если вы не инженер, конструктор, прогер (в некоторых разделах), экономист, аналитик, и прочее .
То экспонента вам в жизни не понадобится…

Вообще-то, есть одна тема, где понимание экспоненты может помочь. Тема, с которой сталкиваются все.
Она может помочь в мегаважном вопросе –

Положили вы в банк 1000 рублей под 10 процентов годовых.
То есть, за год вклад увеличится в 1,1 раза.
Через год будет 1000*1,1 =1100. Небольшая прибыль за то, чтобы отдать кому-то свои кровные.
А если надолго? Тоже мелочь какая-то, вложить лет на 30 и получить что, 3000 сверху? Да нафига?
Вот здесь останавливается большая часть людей которые задумались над тем чтобы как-то преумножать доходы. Но проблема то в том что считается все по-другому!
Но вот тут-то фишка работает по-другому. Ведь в следующий раз проценты начисляются от нового вклада, от 1100
1000*1,1^2 =1221 а не 1200. Вообще, кажется, мелочь, но это не так.
За 30 лет вклад увеличится в 17 раз, а за 40 – в 45!
А если вкладывать под 20 процентов то вклад увеличится в 40 раз уже за 20 лет
Вроде разница не очень велика, но чем дольше вкладываете, тем круче рост.
Не какая-то там примитивная линейная функция или тормознутая парабола, график растет Экспоненциально. Даша, напомни, пожалуйста.

Это ярче всего описывает история, как индейцы продали остров Манхеттен буквально за бусы.
Ну,не то что за бисер. за товары общей стоимостью в 60 гульденов (около 24 долларов, на современные – это около 700). Одеяла, котлы, топоры, ножи и . вампум (индейский бисер, который у них шел вместо денег)

И это приводят в пример того, как белые обманули индейцев. Ибо теперь Манхеттен стоит больше 50 000 000 000 $ . А купили за 30$.
Но, все не так однозначно.
Если бы индейцы положили в банк 30 баксов под 6 процентов годовых, то за 400 лет получили бы почти 400 млрд долларов!
30*1,06^400 = 397 619 212 307
И могли бы скупить весь Манхеттен на корню вместе со всем содержимым.
Есть ощущение, что к этому моменту народ постарше начинает кипеть

Тут есть важный нюанс – все это работает, если экономика и государство находятся в худо-бедно стабильном и рыночном состоянии.
Например, в США частенько были проблемы с финансами и гиперинфляцией. Так в 1865 г., после Гражданской войны, сбережения многих вкладчиков банков резко обесценились и стали мизерными. 150 лет назад.
А у нас, было как

Ну и по мелочи – 1998, 2014


Но страна-то сменилась. И теперь можно делать стандартные для инвестиций штуки, чтобы минимизировать риски: диверсификация активов, инвестирование в разных валютах и в компании разных стран.
Чтоб, если и профукать все деньги, то только, если вся Земля разом обанкротится.
А вместе оно веселей.
Да,много сложностей- и учиться инвестициям,и опасности- пирамиды, санация банков, падение рынка. Поэтому, кстати и не говорю про проценты более 20 в год- там са-а-а-авсем другие уровни рисков. Но если серьезно сесть и посчитать- 20 процентов в год,если планировать на сколько-нибудь долгий период,очень даже неплохо!
Фонд Уоррена Баффета на протяжении около 50 лет давал среднюю доходность в 20 процентов годовых,. и вот он один из трех самых богатых людей мира, в 2008 и вовсе потеснивший с первого места Билла Гейтса.
Вообще, в европейских странах, не так запуганных этим «Вжух»,
С первой зарплаты народ начинает вкладывать на свадьбу-рождение-обучение детей.
Ну, а что делать, если денег нет? И получить хочется быстрее, чем через 30 лет?
Можно заработать, запустить свое дело.
Но чтобы заработать денег – надо деньги. Стартовый капитал, так его.
Взять его можно у тех, у кого деньги уже есть


Есть более безопасный способ.
Прийти к инвесторам и сказать, дайте денег.
И когда вы пойдете просить денег, вдруг окажется, что права была Марь Петровна, приговаривая
« Учи Сидоров, экспоненту! В жизни пригодится»
Ибо люди, которые дают другим деньги на бизнес, редко когда оказываются совсем уж дебилами.
У дебилов просто не будет много денег. Ну… в теории.
И инвесторов нужно убедить, доказать, что ваш проект – хорошая инвестиция.
И вот тут-то и нужна, оказывается, математика, в том числе, экспонента.
По экспоненте, при хорошей конъюнктуре растут продажи и доход.
Для того, чтобы захватить мир, Макдональдсу оказалось достаточно расти на 15 процентов в год на протяжении 45 лет с 1950 до 1985.
И если бизнес сможет расти по экспоненте хотя бы несколько лет – это уже очень круто.
(то не какая-то абстрактная теория, это вопросы одного из моих взрослых учеников, который запускал новый бизнес. Готовил бизнес-план для представления инвесторам. Математикой занимался «для себя»)
Не всегда это работает, но без четкого плана, как и сколько зарабатывать, денег обычно не дают.
Рост акций Эппл. Похоже?

В общем, экспонента – это классная тема)
Следующий пост – про падающую экспоненту и о том, почему мы не пользуемся искусственным золотом (почти).
*Строго говоря, экспонента – это график e^x, где е
2,7… (число Эйлера)
Это число и называется экспонентой.,равно как и график. А те что здесь в математике называются показательной функцией. Но в обычной жизни все графики, которые растут пропорционально иксу часто обзывают общем названием экспонентой, а рост графика — экспоненциальным ростом,ибо растет похоже на график e^x. Почему именно 2,7? Об этом как-нибудь в другой раз.
Найдены дубликаты
>Положили вы в банк 1000 рублей под 10 процентов годовых.
А потом вспомнили, что инфляция — 11%.
И вляжные мечты про богатство по экспоненте нахаляву превращаются. Превращаются. В элегантную нищету.
Очень интересно,когда будет про падающую экспоненту?
Я, когда преподавал студентам, давал им задачку — на стандартном виндовом калькуляторе показать мне число е. Никто не справился, увы. А ведь вроде бы на программистов обучались они. А вы, ТС, сможете? 😉

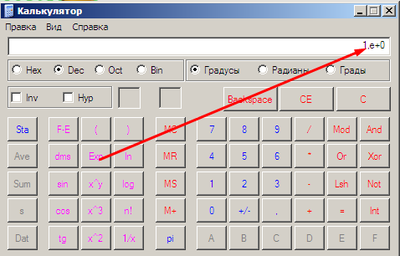
Inv (инверсия) надо нажать, там появится функция e^x, ее применить к единице.
На хрюше уже давно не работал, на семерке именно так. Возможно, из-за неинтуитивности этого и студенты не догадались, и изменили калькулятор в более поздних версиях.
А какая самая быстрая функция?
Нет такой, для любой функции найдется функция, растущая быстрее. Недолго думая, для f(x) можно взять x*f(x).
Величайшие задачи
Все мы несомненно хотя бы раз в жизни слышали о теореме Ферма,теореме Пуанкаре,теории Янга-Миллса.
Для многих из нас эти задачи так и заканчиваются на названиях и многим из нас это кажется чем-то нереальным ,далёким.
В данной статье пойдет речь о книге
Иэна Стюарта «Величайшие математические задачи»

В этой книге автор с невероятной простотой объяснения пишет о самых тяжёлых задачах человечества.
К примеру мне (как ученику средней школы) понравилась глава посвященная Гипотезе Голдьбаха, объяснение началось с простых понятий и правил,которые постепенно перешли в историю гипотезы и попытки ее решить.
Несмотря на достаточно большой объем книги (ок 500 стр),книга читается легко и крайне захватывающе.Также в данной книге автор отвечает на вопрос о том занимает ли математика важную роль в нашей жизни,сам ответ на этот вопрос выражен в множестве примеров.
Эта книга несмотря на с первого взгляда свою однотемность имеет множество тем которые переходят из одной в другую.
Эта книга на мой взгляд является ярким примером хорошего нон-фикшна
Магия чисел
жена занимается репетиторством. Иногда приносит забавные истории.
Задала мальчику на дом задание, в котором была такая задача:
«в классе 32 ученика. Прошла контрольная по математике.
одна восьмая учеников написала контрольную на 5, половина учеников класса — на 4, остальные — на 3.
Сколько учеников написали работу на 3 балла?«
Мама мальчика решила помочь ребенку сделать это домашнее задание(!)
блин! у меня уже здесь глаз дернулся. Ты платишь деньги, чтоб твоего сына учили математике и за свои деньги решаешь ему задачи.
Это ладно. Суть решения, которое было принесено.
1) 32 : 8 = 4. Четыре ученика получили «5». Пока логично. Дальше начинается магия. следите за руками.
2) 4 * 4 = 16. Шестнадцать учеников получили «4». Здесь у моей жены начинали дергаться два глаза. Мальчик рассказывает, как ему объяснила мама: Ну первая четверка в выражении — это мы берем результат из первого действия, вторая четверка — это «4» из условия задачи. Нам же надо найти число тех, кто получил четверку. Вот мы умножаем 4 на «4» и получаем 16. 16 — это же половина от 32.
3) 4 * 3 = 12. Двенадцать учеников получили «3». Внимательный читатель уже понял логику: Первая четверка — мы получили ее в первом действии, а «3» — это тройка из условия, мы же ищем троечников.
Ответ: 12 учеников получили тройку. Правильно? — Правильно!
Мама — умница? Да! нет!!
Вечером жена позвонила этой мамашке, попросила не вмешиваться в домашку совсем.
А я предложил вместо 32 учеников использовать большое число.
А еще вместо «5», «4» в условии используются теперь слова «отлично» и «хорошо».
 yacc11
yacc11
yacc11
- Recent Entries
- Friends
- Profile
- Archive
- Tags
- Memories
Короновирус и матанализ — экспонента ли ?


После того, как набралась некоторая статистика по короновирусу по сети массово стали гулять оценки роста заражения. Как правило они основаны на экспоненте, но так ли это ?
Типичный пример нам предлагает тот же Фрицморген
https://olegmakarenko.ru/1827235.html
который не поленился что-то рассчитать в Excel.
Однако давайте сначала подумаем — а почему экспонента?
Ответа тут ровно два:
1) она вписывается в простую модель геометрической прогрессии
Простая модель выглядит на пальцах так
- допустим у нас есть один зараженный в начале
- за один день зараженный заражает одного человека
- это повторяется
Тогда имеем:
- в «нулевой» день — 1 человек
- на первый день — 2 человека ( один заразил другого )
- нв второй день — 4 человека ( двое заразили каждый по одному )
- на третий день — 8 человек ( четверо заразили четверых )
- И так далее
Количество зараженных человек в день Х выражается по формуле геометрической прогрессии, которую проходили еще в школе : два в степени Х Ее же можно представить и через экспоненту (1)
2) она очень легко аппроксимируется
До короновируса обычно среди большинства «прогнозистов» преобладала линейная модель. Т.е. берем набор известных точек, аппроксимируем ее линейной функцией (2)
Тем более что в том же Excel эта линейная аппроксимация уже есть в виде готовых функций. В случае же более быстрого роста такая модель не подходит и вот ей на замену приходит экспонента, потому что она тоже очень легко аппроксимируется.
Пусть у нас зависимость имеет вид константы умноженной на экспоненту в показателе которой стоит некоторый множитель, множитель перед экспонентой легко внести в саму экспоненту (3) и такой вид более простой для аппроксимации.
В самом деле: ее можно переписать как (4), а это как раз линейная зависимость. Далее мы вычисляем логарифм от известного количества зараженных и считаем а и b. Составить прогноз после этого совершенно легко.
. и он гуляет по сети, причем особенно весело смотреть на графу «отставание в днях»
Вспоминаем матанализ
В старших классах в школе преподавали основы анализа ( математического ).
Более чем уверен, что многие, кто это проходил в школе, благополучно его забыли — на практике же производные почти не используются.
Однако мы вспомним.
Итак, если у нас есть количество зараженных суммарно по дням, то первая производная будет показывать число заражений в день. А вторая — скорость изменения числа зараженных в день
Экспонента тут выделяется тем, что какую производную от нее не возьми — она останется экспонентой (5)
Т.е. и десятая производная от е в степени х останется е в степени х
Если же в экспоненте стоит линейная функция, то множитель при х переходит в множитель перед экспонентой (6)
Вот и давайте положим нашу «экспоненту» на хирургический стол и препарируем ее по матанализу.
А именно давайте взглянем на вторую производную. Для ее получения надо от прироста текущего дня отнять прирост предыдущего.
Для данных я буду брать Москву, как самый тяжелый регион России
Итак, вот график того, что получилось.
Как можно видеть на экспоненту он совсем не похож. Более того — это и не может быть экспонентой вида (4) ибо она строго положительная, а тут есть отрицательные точки. И даже если мы их выкинем — то все равно экспонентой она не станет.
Зато этот график очень напоминает то, что интернет-эксперты любят аппроксимировать — курсы валют. Чтобы показать что «в среднем» доллар растет — тут самое место применить линейную аппроксимацию вида (7) и она тут подойдет в первом приближении.
Лирическое отступление — Метод Наименьших Квадратов
Чтобы аппроксимировать функцию обычно применяется Метод Наименьших Квадратов.
Суть этого метода можно наглядно показать следующим образом : Надо так подобрать аппроксимирующую функцию, которая не обязана проходить через экспериментальные точки, чтобы сумма квадратов отклонений от нее до экспериментальных точек — на картинке это зеленые отрезки к реальным данным в виде красных точек — была минимальна. Поскольку отклонения могут быть как вверх так и вниз, то берут их квадрат, который всегда будет положителен.

Как я уже говорил, в Excel функция линейной аппроксимации встроена и легка в использовании.
Сумма квадратов таких отклонений называют Ошибкой.
Идем от старшей производной
А теперь пора опять вспомнить матан: если вторая производная выражается линейной функцией вида (7) то какой функцией будет выражаться первая производная ?
Правильно! — квадратичной, вида (8)
Квадратичная функция по другому называется Квадратный Трехчлен — ее в школе изучают и о ней ходит много шуток. Если оставить только старшую степень то график будет представлять параболу и тоже знаком школьникам.
Собственно оригинально у меня идея этого поста и возникла когда я аппроксимировал количество новых заражений квадратичной функцией при обсуждении с друзьями.
И вот аппроксимировать квадратичную функцию для большинства людей будет проблемой — в школе это не проходят ( в отличии от геометрической прогрессии ) и встроенной функции в Excel нет ибо в подавляющем большинстве аппроксимаций ограничиваются линейной.
Однако с помощью Excel коэффициенты для аппроксимации совершенно нетрудно посчитать
Вот видео, которое объясняет как это делать
Для тех, кто отучился первый курс технического ВУЗа — это линейная алгебра в части матриц и операций с ними. Excel позволяет как рассчитать обратную матрицу, так и делать умножение матрицы на вектор встроенными функциями — надо только рассчитать элементы матрицы через суммы различных степеней и произведений X и Y.
Изначально я аппроксимировал квадратичную функцию по данным до 12 апреля включительно в Москве.
Вот результаты.

Как можно увидеть при аппроксимации квадратичной функцией ошибка . меньше! Т.е. она лучше описывает динамику процесса.
Потом, уже 18 апреля, я взял ту же функцию и ранее рассчитанную экспоненту и еще раз проверил — как можно видеть — разрыв от экспоненты по ошибке только увеличился и составляет где-то 2.5 раза.
Переходим к кубам
Если первую производную Y’ описывает квадратичная функция вида (8), то какая будет описывать саму Y ?
Правильно! — кубическая, вида (9)
Если оставить старшую степень то это тоже известно школьникам — это гипербола. Аппроксимация кубической функции после того, как вы поигрались с матрицами при аппроксимации квадратичной — не представляет труда. Просто будет матрица 4х4 а не 3х3 и тот же самый принцип.
Берем данные Москвы по суммарному количеству зараженных по 15 апреля включительно и вычисляем коэффициенты для кубической аппроксимации и аппроксимации экспонентой. А потом выводим на график.

Как наглядно видно — куб очень точно отражает реальные данные. А еще лучше посмотреть на ошибку — она отличается почти на два порядка в пользу кубов.
Почему все это я вспомнил? А потому что куб отличается от экспоненты гораздо меньшей скоростью роста.
Т.е. если у нас на 20 апреля 20 754 зараженных, то через неделю экспонента дает 67 599 а куб — 41 128. А еще через три недели экспонента уже дает 1 962 966 а куб — 212 023. Разница уже почти на порядок.
По факту на графиках мы видим а-ля гиперболу, а НЕ экспоненту.
Разумеется за приведенным кубом нет никакой модели с моей стороны — модели эпидемий гораздо более сложные с точки зрения математики. Более того — как куб так и экспонента растут неограниченно, а количество зараженный на Земле не может превышать всего населения -реальная формула должна этот предел учитывать, как и перегиб на уменьшение.
Данный пример наглядно показывает, что в глубине может лежать то, что не видно на поверхности, но даже уже простым анализом это видно — что сейчас рост вовсе не экпоненциальный.
Аналогично можно посмотреть и случай всей России — и там куб тоже будет сейчас описывать лучше экспоненты, с ошибкой на порядок меньше

Сегодня Фрицморген вставил график изменения прироста по дням, но этот прирост выражался в процентах т.е. отношение количества новых к количеству заражений за предыдущий день.
https://olegmakarenko.ru/1837346.html
Такой график не дает никакой информации, а смотреть надо на абсолютные значения в динамике — по ним наглядно видно, что рост продолжается и точка перегиба еще не достигнута — пандемия продолжается в России хотя и не экспонециальными темпами.

В самом деле, если, на примере Москвы, рассчитать такое отношение для экспоненты то мы получим что такое отношение должно равняться Е в степени a минус один и оставаться константой.
Однако если посмотреть на динамику этих коэффициентов с начала, то окажется что а падает, а b наоборот растет.
Более того, если мы рассчитаем a по скользящему окну в десять дней назад относительно текущей даты, то он колеблется но вовсе не снижается.

Все это свидетельствует только о том, что модель экспоненты очень хреново подходит для описания динамики, а не о том, что «экспоненциальный рост» замедляется.
Вывод:
Пользуйтесь самоизоляцией и освежайте то, чему вас учили на уроках математики.
Добавление:
Специально для тех, кто упирается в полулогарифмическую шкалу: Я взял аппроксимированные экспонентой данные по Москве по суммарному количеству зараженных ( из раздела кубов ), округлил до целых чисел, вычислил сначала первую, а потом и вторую производную
Далее я просто построил график

Как можно видеть, поскольку оригинальные данные считались по экспоненте, то и во второй производной она никуда не делась.
Построение графика в полулогарифмической шкале недостаточно для констатации факта экспоненты.
Что такое Экспонента
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
График экспоненты выглядит следующим образом:

Для чего используется экспонента?
Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.
Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
- через сумму ряда;
- через формулу Муавра — Стирлинга;
- другие.
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.
Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как  .
.
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Узнайте также, что такое Число Пи и Логарифм.
Экспонента и число е — реальные примеры из жизни
В прошлой статье мы рассмотрели различные коэффициенты роста экспоненты. Давайте теперь посмотрим, где это всё используется в реальной жизни.
Время примеров!
Примеры всегда делают сухую математику веселее. Маленькая поправка: мы так уже привыкли к формулам типа 2 x и обычному, составному росту, что можно легко запутаться (я и сам через это прошел). Почитайте подробнее о простом, составном и непрерывном росте.
Эти примеры демонстрируют плавный, непрерывный рост, а не «скачкообразный» рост, которые происходит в годичные интервалы. Есть способы расчетов прибыли между интервалами, но оставим это для новой статьи.
Пример 1: Наращивание кристаллов
Предположим, у меня есть 300 кг магических кристаллов. Они магические, потому что растут в течение дня: сначала я вижу один кристалл, а через 24 часа он выбрасывает из себя другой кристалл, весом как он сам. (Кристаллы-детки начинают расти сразу же, и с таким же темпом, но я это уже не могу отследить — я могу увидеть только вот эту первую партию новорожденных). Сколько кристаллов будет у меня через 10 дней?
В общем, так как кристаллы начинают расти немедленно, мы имеем дело с непрерывным ростом. Наш коэффициент прироста 100% каждые 24 часа, так что через 10 дней мы получим 300 × e 1 × 10 = 6.6 миллионов кг магических самоцветов.
Здесь может быть загвоздка: видите, какая разница между исходным коэффициентом и общим коэффициентом прироста. «Исходный» — это насколько изменяется один кристалл: 100% за 24 часа. Общий прирост равен числу е (2.718х), потому что детки-кристаллы тоже постоянно растут.
В этом случае у нас есть исходный коэффициент (как быстро растут кристаллы), и мы хотим получить совокупный результат (как вся группа вырастет с учетом кристаллов-деток). Если у нас есть общий прирост, а вычислить требуется исходный коэффициент (рост одного кристалла за определенный период времени), мы вычисляем в обратном порядке и используем натуральный логарифм.
Пример 2: максимальная ставка процента
Допустим, у меня есть 120 рублей на счету в банке с 5% ставкой. Мой банк очень щедр, и обеспечивает мне максимально возможную капитализацию. Сколько у меня будет денег через 10 лет?
Наша ставка составляет 5%, и нам повезло с непрерывной капитализацией. После 10 лет мы получим 120 × e 0.05 × 10 = 197,85 рублей. Конечно, большинство банков не настолько хороши, чтобы предоставить вам лучший из возможных процентов. Разница между вашей конечной суммой и размером непрерывного прироста показывает, насколько именно они жадничают..
Пример 3: радиоактивный распад
У меня 10 кг радиоактивного материала, который непрерывно распадается с коэффициентом 100% в год. Как много у меня останется через 3 года?
Совсем ничего? Ноль без палочки? Подумайте еще раз.
Распадаться непрерывно на 100% в год — примерно такую ситуацию мы рассматривали в начале. Да, мы начали с 10 кг, и ожидаем потерять все к концу первого же года, так как материал распадается на 10 кг/год.
Наше радиотопливо распадалось несколько месяцев, и осталось всего 5 кг материала. До полного распада осталось полгода? Неа! Теперь мы теряем в весе уже 5 кг/год, так что у нас еще целый год для полного распада!
Мы ждем еще несколько месяцев, и доходим до 2 кг. И конечно же, дальнейший распад уже пойдет со скоростью 2 кг/год, так что у нас еще в запасе полный год (с этого момента). Мы доходим до 1 кг, и опять в запасе целый год, так мы достигнем 0,5 кг, еще один год – улавливаете схему?
С течением времени мы теряем материал, но и скорость распада постепенно уменьшается. Этот постоянно изменяющийся темп и лежит в основе непрерывного роста и распада.
Спустя три года, у нас останется 10 × e -1 × 3 = 0.498 кг. Мы использовали отрицательную степень для распада – нам нужна дробь (1/e п × в ) вместо произведения роста (е п × в ). (Распад обычно дается в контексте «полураспада» — мы поговорим о преобразовании этих показателей в другой статье).
Больше примеров
Если вы хотите более сложные примеры, попробуйте формулу опционов Блэка-Шоулза (число е используется для экспоненциального снижения в цене) или радиоактивный распад. Цель таких примеров — дать человеку увидеть е п × в в формуле и понять, почему она там: это и моделирует прирост или распад.
Сейчас вы знаете, почему константа называется «е», а не «пи» или другое какое-то число: е, возведенная в степень «п × в», позволяет оценить влияние коэффициента прироста П и времени В.
Еще многому предстоит научиться!
Моей целью было:
- Объяснить, почему так важна константа е: это фундаментальная константа, как «пи», которая отражается в темпах роста.
- Дать понятное, логическое объяснение: число е дает вам увидеть влияние любого коэффициента роста. Каждый новый «кусочек» (вспомните наших цветных друзей на графиках) делает свой вклад в общий прирост.
- Показать, где это используется: e x позволяет предсказать, как повлияет определенный коэффициент роста и период времени на имеющуюся величину.
- Разжечь ваш аппетит перед следующим блюдом: в будущих статьях мы изучим другие свойства числа е.
Эта статья – только начало. Если попытаться впихнуть все в одну страничку, это утомит моих читателей, и мне самому станет скучно. Стряхните с себя пыль, отвлекитесь и узнайте много интересного о близнеце числа е — натуральным логарифмом.