Примеры разделения датасета на train и test c Scikit-learn

Как отстроить Fender Stratocaster: Часть 4. Высота струн, звукосниматели, мензура

Всем привет! Сегодня вдруг вспомнил, что так и не закончил переводить статью «Как отстроить Fender Stratocaster».
Что ж, спешу исправить это недоразумение. Сегодня заключительная часть, где речь пойдет про регулировку высоты струн, отстройку высоты звукоснимателей и настройку мензуры.

Шаг 7. Регулировка высоты сёдел бриджа

Далее подрегулируем высоту струн, выставив сёдла на бридже по высоте. Регулировочные винты на бридже могут быть разными, так что используйте тот ключ, который поставлялся с вашей гитарой. Для этого Страта я использовал шестигранный ключ на 0,050”.

1. Настройте гитару в нужный строй.
2. На 1-й лад поставьте каподастер.
3. Измерьте расстояние до струны над 12-м ладом, используя спец. инструмент или просто железную линейка так, как описано в Шаге 1.
4. Начинайте регулировку высоты сёдел с первой струны, поворачивая регулировочные винты. Этими винтами можно поднять или опустить высоту струны до нужной высоты (Фото 14).

Для современных Stratocaster с радиусом накладки 9,5” – 12”, официальная спецификация Fender – это 4/64” (1, 59мм) над ладом, как для 1-й, так и для 6-й струны. Однако, повторюсь, что это величина может меняться в зависимости от ваших предпочтений, стиля игры и калибра струн. После каждой регулировки, заново подстройте струну с которой вы работали и сделайте измерения еще раз.

5. Повторяйте эту процедуру для каждой струны, пока вы не добьётесь нужной высоты. В конечном итоге, нужно постараться добиться того, чтобы струны описывали дугу с радиусом равным радиусу накладки грифа. (Многие делают это на глаз, однако если вы хотите делать это точно, то можно купить специальный инструмент.)

На этой гитаре высоты первой струны я выставил в 3/64” (1,19 мм) и 4/64” (1,59 мм) — для шестой. Эти значения немного больше тех, которые я обычно выставляю, но для владельца они были комфортны, к тому же отлично подошли к его 0,012” комплекту струн.

Шаг 8. Регулировка высоты струн у верхнего порожка

Итак, мы приближаемся к концу! После установки нужной высоты всех шести струн регулировкой сёдел на бридже, обратим свой взгляд к верхнему порожку. Очень важно, что и тут струны были на нужной высоте. Если струны тут стоят высоко, то их будет сложно зажимать, следовательно, и играть будет тоже сложно.

1. Уберите каподастр с первого лада.
2. Настройте гитару.
3. Измерьте высоту каждой струны над первым ладо (расстояние от верха лада то нижней точки струны). Для первой струны высота должна быть около 1/64” (0,4 мм) и 2/64” (0,79 мм) — для шестой. Каждая более толстая струна должна быть немного выше, чем предыдущая более тонкая.
4. Для того, чтобы опустить струну на нужную высоту, нужно немного прорезать пазы в порожке, использует надфиль нужного размера. (Такие надфили тоже можно купить в спец. магазинах).

Делайте пропил аккуратно, особенно уделяя внимание углу надфиля по отношению к порожку. Угол должен быть точно такой же, как у проходящей через порожек струны. Если этот угол не выдержать, то струна не сядет в паз идеально и могут возникнуть, как проблемы со строем, так и со звуком.

Удостоверьтесь, что струна не застревает в пазе. Она должна двигаться свободно. Если же струна все же застревает, то аккуратно поворачивайте надфиль в пазу из стороны в сторону, что чуть-чуть его расширить. После нескольких движений надфилем, установите струну в паз, настройте её и измерьте высоту струны на 1-м ладом.

5. Повторите процедуру для каждой струны, используя надфиль нужного размера.

Т.к. на этот страт мы установили струны более толстые, чем тут стояли до этого, то мне пришлось немного расширить пазы в порожке, чтобы струны сели как нужно.

Шаг 9. Настройка высоты звукоснимателей

При отстройке гитары, регулировку высоты звукоснимателей зачастую опускают. Тем не менее, если датчики располагаются близко к струнам – это может вызвать их дребезг, а также проблемы с настройкой мензуры. Если же звукосниматели стоят слишком далеко от струн, то сигнал может быть довольно слабым.

Вот какие значения должны быть на для каждого звукоснимателя на Стратокастере.

А вот моя система настройки высоты звукоснимателей.

1. Зажмите 1-ю струны на последнем ладу. С помощью линейки измерьте расстояние от выступающего сердечника до нижней точки струны. Настройте нужную высоту, с помощью винта звукоснимателя со стороны тонких струн. (Фото 16).
2. Зажмите 6-ю струну на последнем ладо, точно так же измерьте и настройте высоту у толстых струн.
3. Повторите процедуру для среднего и нэкового звукоснимателя.

Шаг 9. Настройка мензуры

После того, как мы настроили высоту звукоснимателей, самое время перейти к настройке мензуры. Примечание: перед настройкой мензуры убедитесь, что у вас стоит свежий комплект струн. Если струны старые, то перед отстройкой лучше их заменить.

В конечном счете, настройка мензуры сводится к перемещению сёдел бриджа ближе или дальше к верхнему порожку. Регулировочные винты находятся сзади тремоло. Чтобы двигать седла нужна маленькая отвертка крестом. Затягивая винт (по часовой стрелке) мы двигаем седло назад, тем самым увеличивая длину струны, отпуская винт (против часовой стрелки) мы двигаем седло вперед, укорачивая струну. (Фото 18)

1. Вооружитесь хорошим тюнером и настройте каждую струну. Но теперь, вместо того, чтобы настраиваться по открытой струне, возьмите натуральный флажолет на 12-м ладу и настройтесь по нему.
2. Теперь начиная с первой струны, играйте флажолет на 12-м ладу, затем зажмите эту же струну на 12-м ладу и сыграйте ноту. Если нота по отношению к флажолету будет высить, то отодвиньте седло назад от порожка, если же, наоборот – нота будет ниже, то придвиньте седло ближе к порожку. После каждого передвижения седла нужно заново настроить струну и снова проверить ноту на 12-м ладу и флажолет на том же ладу. Таким образом, нужно добиться полного совпадения ноты и флажолета на 12-м ладу.
3. Повторите процесс для каждой из шести струн.

На этом, пожалуй, отстройку гитары можно считать законченной. И самое время приступить к тест-драйву. Не исключено, что через некоторое время вам захочется что-то поменять. Например, натяжение пружин тремоло, высоту звукоснимателей, прогиб грифа или высоту сёдел. И хорошо то, что Страт позволяет все это настраивать.

Однако помните, что изменение какого-то одного элемента системы может вызвать потребность в настройке и другого элемента. Так что, если вы что-то поменяли и чувствуете, что что-то не так, то возможно стоит немного обождать, сделать глубокий вдох и посмотреть на все эти 10 шагов. В конце концов всегда можно начать с начала.

В конце концов, вы начнете на подсознательном уровне чувствовать, как элементы взаимодействуют между собой, и это чувство позволит отстроить вашу гитару именно так, как нужно лично вам.

Автор: John LeVan. Гитарный мастер и техник из Нэшвила. Написал 5 книг по ремонту гитар.
[premierguitar.com]

Случайное перемешивание строк

Первое, на что следует обратить внимание: перемешаны ли ваши экземпляры? Это следует делать пока нет причин не перетасовывать данные (например, они представляют собой временные интервалы). Мы должны убедиться в том, что наши экземпляры не разбиты на выборки по классам. Это потенциально вносит в нашу модель некоторую нежелательную предвзятость.

Например, посмотрите, как одна из версий набора данных iris, упорядочивает свои экземпляры при загрузке:

Если такой набор данных с тремя классами при равном числе экземпляров в каждом разделить на две выборки: 2/3 для обучения и 1/3 для тестирования, то полученные поднаборы будут иметь нулевое пересечение классовых меток. Это, очевидно, недопустимо при изучении признаков для предсказания классов. К счастью, функция train_test_split по умолчанию автоматически перемешивает данные (вы можете переопределить это, установив для параметра shuffle значение False ).

• В функцию должны быть переданы как вектор признаков, так и целевой вектор (X и y).
• Для воспроизводимости вы должны установить аргумент random_state .
• Также необходимо определить либо train_size , либо test_size , но оба они не нужны. Если вы явно устанавливаете оба параметра, они должны составлять в сумме 1.

Вы можете убедится, что теперь наши классы перемешаны.

Enlisted вылетает в случайный момент или при запуске

Ниже приведено несколько простых способов решения проблемы, но нужно понимать, что вылеты могут быть связаны как с ошибками игры, так и с ошибками, связанными с чем-то определённым на компьютере. Поэтому некоторые случаи вылетов индивидуальны, а значит, если ни одно решение проблемы не помогло, следует написать об этом в комментариях и, возможно, мы поможем разобраться с проблемой.

• Первым делом попробуйте наиболее простой вариант – перезапустите Enlisted, но уже с правами администратора.

Как увеличить объём памяти видеокарты? Запускаем любые игры

Большинство компьютеров и ноутбуков имеют интегрированную (встроенную) графическую карту. Но для работы видеоадаптера используется лишь часть.

Постанализ: CUPED

CUPED (Controlled-experiment Using Pre-Experiment Data) — очень популярный в последнее время метод уменьшения вариации. Основная идея метода такова: давайте вычтем что-то из теста и из контроля так, чтобы математическое ожидание разницы новых величин осталось таким же, как было, а дисперсия уменьшилась.

A и B — некоторые случайные величины (ковариаты). Тогда утверждается, что если θ будет такой, как указано в формулах далее, то дисперсия будет минимально возможной для таких статистик:

В случае выборок разного размера:

Формула для дисперсии:

То есть, чем больше корреляция по модулю, тем меньше будет дисперсия.

Также важно помнить: чтобы метод работал корректно, необходимо и достаточно, чтобы математические ожидания A и B совпадали.

Осталось понять, что брать в роли A и B. Чаще всего для них берут значения той же метрики на предэкспериментальном периоде. Например, вы смотрите метрику выручки, тогда в роли ковариаты A и B можно взять выручку от пользователя за месяц до начала эксперимента. Чем хорош такой способ:

Математическое ожидание метрики на предпериоде будет одним и тем же в тесте и в контроле — иначе у вас некорректно поставлен A/B-тест. А значит, и CUPED даст правильный результат.

В большинстве случаев метрика на предпериоде сильно коррелирует с экспериментальным периодом. Отсюда получается, что и дисперсия сильно уменьшится.

Кроме значения метрики на предпериоде можно использовать результаты ML-модели, обученной предсказывать истинные значения метрик без влияния тритмента. С хорошей моделью можно достичь большего уменьшения дисперсии.

Теперь, когда мы определились с новой метрикой, надо понять, какой критерий использовать. Можно точно также использовать T-test для CUPED-метрик. Вот результаты проверок на искусственных тестах:

Проверка корректности метода на AB, AA тестах

Реальный уровень значимости: 0.0513; доверительный интервал: [0.0489, 0.0539].

Результаты для A/A-тестов: реальный уровень значимости: 0.0486; доверительный интервал: [0.0462, 0.0511].

Про используемую процедуру проверки критерия можно прочитать в первой части статьи.

Давайте ещё посмотрим, на сколько в искусственном примере уменьшилась ширина доверительного интервала по сравнению с обычным T-test:

Отношение ширины доверительных интервалов друг к другу: 11.015%.

Мы сократили доверительный интервал примерно в 10 раз! В этом примере мы очень сильно увеличили мощность критерия, перейдя от T-test к CUPED-критерию. А ещё, CUPED состоит всего из четырёх строчек кода!

Также, часто в некоторых статьях предлагают следующую метрику для CUPED:

Вместо ковариаты B, объявленной ранее, подставляется значение этой метрики на предпериоде, из которого вычтено среднее значение. Тогда математическое ожидание этой ковариаты будет нулевым, а математическое ожидание новых штрихованных метрик совпадает с математическим ожиданием начальных метрик:

Кроме того, в этот момент вы не теряете бизнес-смысл у вашей новой CUPED-метрики, и можете посчитать оценки и доверительные интервалы для вашей метрики в тесте и в контроле.

Так вот, запомните: никогда не используйте такую CUPED–метрику! Покажу, к чему это может привести.

Сначала посмотрим, сколько раз истинное математическое ожидание C не попало в доверительный интервал для математического ожидания C»:

Не попал в 85.2% случаев; доверительный интервал: [82.86%, 87.27%].

Новая метрика имеет другое математическое ожидание, нежели изначальная (в тех предпосылках, на которых работает t-test и на которых строится доверительный интервал через ЦПТ)! Это значит, что вы не можете использовать доверительный интервал этой статистики для оценки среднего у начальной метрики.

А теперь посмотрим, что в этот момент покажет CUPED-критерий:

Реальный уровень значимости: 0.8964; доверительный интервал: [0.8929, 0.8998].

Ошибка будет больше, чем в 80% случаев!

Получается, что метрика как портит CUPED-критерий, так и не даёт правильную оценку изначальной метрики.

> Доказательство и выводы из него

Давайте вспомним, в каком предположении работает T-test, а также строится доверительный интервал для случайной величины по выборке? В предположении о независимости элементов, где как раз и кроется ошибка. Давайте немного поколдуем.

Возьмём случайную величину mean(C_b) и размножим её на выборку размера N, что мы и делаем в рассматриваемой CUPED-метрике. Посчитаем математическое ожидание и дисперсию выборки в предположении о независимости её элементов.

В таком случае дисперсия будет равна 0, ведь вся выборка состоит только из одного значения.

Математическое ожидание: вне зависимости от размера N, среднее у этой выборки будет равно mean(C_b), а значит, по усиленному закону больших чисел математическое ожидание выборки будет равно текущему полученному значению mean(C_b), а не истинному матожиданию C_b.

Думаю, вы поняли, к чему я клоню. В предположении о независимости выборок получаются следующие результаты:

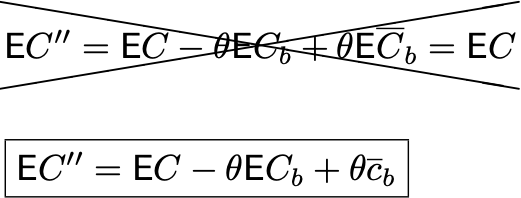
Где c_b — полученное значение среднего на предпериоде.

То есть алгоритм построения доверительного интервала, а также T-test ожидают получить на вход такую выборку:

Где различные индексы отвечают за разные наблюдения. А мы вместо этого передаём такую выборку, внимание на индекс у mean(C_b):

Поэтому и возникает продемонстрированная ранее ошибка.

Итого: в предположении о независимости, CUPED-метрика с вычитанием среднего значения приведёт вас к неверному результату! А зависимость элементов выборки очевидно следует из того, что у вас используется одна и та же случайная величина при создании каждого элемента выборки.

Теперь, посмотрим, как решить этот вопрос:

Не использовать такую CUPED-метрику.

Намучиться, пострадать, но самостоятельно выписать дисперсию для среднего этой метрики, учитывая все ковариации и зависимости в данных. Возможно, получится корректный критерий, если вы не ошибётесь.

Реализовать через бутстрап. И тогда подобная ковариата работает.

Причём варианты два и три не несут в себе глубокого смысла, потому что по мощности их критерии не будут выигрывать у аналогов без вычитания среднего.

Относительный CUPED

Осталось показать, как настроить CUPED для относительной постановки A/B-тестов. И здесь всё будет не так гладко.

Предлагается посмотреть на следующую нетривиальную статистику:

Причём в числителе штрихованные CUPED — случайные величины без вычитания среднего у ковариаты, а в знаменателе — обычное среднее на контроле, без штрихов. Знаменатель такой, потому что CUPED-метрика не сохранит изначальное математическое ожидание.

Утверждается, что при большом размере выборок эта статистика, как и относительный T-test критерий, будет верно оценивать и строить доверительный интервал для истинного прироста. Доказательство корректности будет практически такое же, как и у T-test критерия из первой части. Дисперсия для такой функции также строится через дельта-метод, а формула практически полностью повторяет формулу для дисперсии в T-test.

Формула дисперсии в случае выборок разного размера

В этот раз код будет не таким простым. Но очень много кусков взято из реализации relative_ttest из первой части.

Реальный уровень значимости: 0.0506; доверительный интервал: [0.0481, 0.0531].

Результаты для A/A-тестов: реальный уровень значимости: 0.048; доверительный интервал: [0.046, 0.0503].

Отлично! Мы смогли построить относительный критерий для CUPED, который корректно работает.

Итого: если вы ещё не используете CUPED для A/B-тестов, самое время это исправить. Пишется не сложнее, чем T-test, но при этом сильно улучшает мощность критериев.

Теперь предлагаю поговорить про бутстрап-аналог CUPED–метода.

Проблема 5

Чтобы узел был осведомлен о том, какие узлы являются активными участниками кластера (то есть о текущем членстве), применяется ряд периодических контрольных сигналов, передаваемых между узлами по сети. Эти пакеты сигналов представляют собой UDP-датаграммы, следующие через порт 3343.

Каждый пакет включает регистрационный номер, по которому отслеживается факт приема пакета. Это работает следующим образом: узел Node1, отправляющий регистрационный номер 1111, ожидает ответного пакета, включающего 1111. Эти действия совершаются между всеми узлами каждую секунду. Если узел Node1 не получает ответного пакета, он отправляет следующий по порядку регистрационный номер (1112), и т.д.

По умолчанию, если узел не получает пять контрольных сигналов в течение пяти секунд, WSFC устанавливает факт отказа узла. Активный узел в кластере отправляет пакет на узел, где установлен отказ, чтобы завершить работу службы кластера, и регистрирует событие 1135 в журнале событий системы (см. экран 7).

Экран 7. Событие 1135 в журнале событий системы

Такое событие может быть вызвано несколькими причинами, многие из которых связаны с блокировкой связи через порт 3343:

1. Отказ сетевого оборудования.

2. Устаревший драйвер или устаревшая прошивка сетевого адаптера.

3. Сетевая задержка.

4. Протокол IPv6 разрешен на серверах, но параметры брандмауэра Windows выключают следующие разрешения для входящего и исходящего трафика:

• основы сетей – объявление поиска соседей;
• основы сетей – запрос поиска соседей.

5. Настройка коммутаторов, брандмауэров или маршрутизаторов не допускает прохождения трафика данных UDP-датаграмм.

6. Проблемы производительности (зависания, задержки и прочее).

7. Неправильно настроенные параметры буфера приема у драйвера сетевого адаптера.

Первым делом я всегда проверяю счетчик отброшенных принятых пакетов в составе объекта производительности сетевого интерфейса в окне системного монитора. Этот счетчик отслеживает число входящих пакетов, которые были отброшены, хотя и не было зафиксировано каких-либо ошибок, препятствующих их передаче протоколу верхнего уровня. Одна из возможных причин – необходимость освободить место в буфере.

Для добавления счетчика отброшенных принятых пакетов в окне системного монитора щелкните правой кнопкой на дисплее и выберите «Добавить счетчики». В открывшемся окне добавления счетчиков укажите нужный компьютер, выполните прокрутку и выберите счетчик «Отброшено принятых пакетов». В выпадающем списке «Экземпляры выбранного объекта» выберите нужный сетевой адаптер и нажмите «Добавить» (см. экран 8).

Экран 8. Добавление счетчика отброшенных принятых пакетов в системный монитор

Добавив счетчик, проверьте его среднее, минимальное и максимальное значения. Если есть значения больше нуля, это указывает на необходимость настройки буфера приема для сетевого адаптера. Проконсультируйтесь с производителем сетевого адаптера по поводу рекомендуемых параметров. Может потребоваться перезагрузка.

В отказоустойчивом кластере Windows Server 2012 R2 можно воспользоваться мастером проверки конфигурации для выполнения проверки сетевого взаимодействия. Этот тест позволяет проверить возможность информационного обмена между узлами через порт 3343. Если есть проблемы связи, то будет выдана соответствующая ошибка с указанием возможной причины.

Теории социальной стратификации

К числу наиболее значимых теорий социальной стратификации относятся: Классовая теория Карла Маркса, трехкомпонентная теория стратификации Макса Вебера, теория стратификации Питирима Сорокина. Рассмотрим каждую из них подробнее.

Классовая теория Карла Маркса

Немецкий философ Карл Маркс считал, что в любом обществе существует всего два класса: эксплуататоры и эксплуатируемые. Он по-своему понимал, что такое социальная стратификация и как она проявляется. Согласно его классовой теории, тот, кто владеет средствами производства и использует наёмный труд, является эксплуататором. Соответственно, тот, кто не владеет средствами производства и работает за зарплату, является эксплуатируемым.

По мнению Маркса, классы находятся в непрерывном противостоянии, и борьба между ними является основной движущей силой истории (а итогом этой борьбы в любом обществе должна стать революция).

Маркс считал, что развитие любого общества состоит из 5 этапов:

• Первобытно-общинный строй. Частной собственности не существовало, следовательно, не существовало и классов.
• Рабовладельческий строй. В частной собственности могли находиться не только предметы, но и люди. Существовало два класса: рабовладельцы и рабы.
• Феодализм. Крестьяне отличались от рабов тем, что формально являлись свободными. Существовало два класса: феодалы и крестьяне.
• Капитализм. Капиталистическое общество, по мнению Маркса, также делится на два класса: капиталисты и рабочие.
• Коммунизм. Общество, в котором нет института частной собственности, а также классового неравенства и противостояния между «эксплуататорами» и «эксплуатируемыми».

Маркс и его сторонники считали коммунизм вершиной развития любого общества. Однако история показала, что подобный порядок невозможно воплотить в реальность по целому ряду причин.